Вопрос 15.
Фононы в кристаллической решетке. Средняя скорость звука
Фонон — минимальная порция энергии, или квант энергий колебательной кристаллической решетки.
Скорость звука — скорость распространения упругих волн в среде: как продольных , так и поперечных.
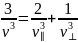
Билет 16.
Свойства фононов в кристаллической решетке; средняя скорость звука, максимальная частота нормальных колебаний кристаллической решетки, функция распределения фононов по частоте.
Фононы и их взаимодействие с электронами играют фундаментальную роль в современных представлениях о физике сверхпроводников, процессах теплопроводности, процессах рассеяния в твердых телах. Модель кристалла металла можно представить как совокупность взаимодействующих осцилляторов, причем наибольший вклад в их среднюю энергию дают колебания низких частот, соответствующие упругим волнам, квантами которых и являются фононы.
;
;
.
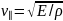- скорости
продольной
волны;
–
скорость
поперечной волны
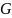- модуль
сдвига (модуль жесткости);
Е – модуль Юнга.
ρ - плотность при н.у.
Билет 17.
Расчет внутренней энергии кристалла с помощью представления о фононах. Предельные случаи высоких и низких температур.
В физике твёрдого тела модель Дебая — метод, для оценки фононного вклада в теплоёмкость твёрдых тел. Модель Дебая рассматривает колебания кристаллической решётки как газ квазичастиц — фононов. Эта модель правильно предсказывает теплоёмкость при низких температурах, которая, согласно закону Дебая, пропорциональна . В пределе высоких температуртеплоёмкость стремится к 3R, согласно закону Дюлонга — Пти.
Модель Дебая = Расчет внутренней энергии кристалла с помощью представления о фононах.
пусть будет, но
лучше не диктовать
Вопрос 18.
Квантовый гармонический осциллятор его энергетический спектр. Расчет энергии нулевых колебаний кристаллической решетки.
Нормальные колебания можно представить как гармонический осицилятор с энергией.
Квантовый гармонический осциллятор — одна из немногих систем в квантовой механике, для которой может быть получено точное решение уравнения Шрёдингера.
Модель квантового гармонического осциллятора служит первым приближением для описания колебательного движения в молекулах. Для более точных расчетов (например, при больших амплитудах колебаний) могут быть использованы более точные модели потенциалов, например, потенциал Морзе.
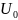- энергия нулевых
колебаний
Билет 19.
Вырожденные и невырожденные коллективы частиц. Параметр вырождения. Оценка параметра вырождения для электронного газа в металле.
Свойства частиц не влияют на свойство коллектива частиц, как целого-невырожденного. Свойство и специфика частиц существенно влияет на свойство частиц.
- не вырожденности
- вырожденности
Билет 20.
Квантовое описание движения свободного электрона в кристаллической решетке, волновая функция, волновой вектор, квазиимпульс, дисперсионное соотношение E(K)
Волновая
функция,
или пси-функция 
— комплекснозначная
функция, используемая в квантовой
механике для описания чистого
состояния системы. Является коэффициентом
разложения вектора состояния по
базису (обычно координатному):
Волновой
вектор — вектор,
направление которого перпендикулярно фазовому
фронту бегущей волны, а абсолютное
значение равно волновому числу.Волновой
вектор обычно обозначается латинской
буквой 
и
величина его измеряется в обратных
метрах (СИ) или обратных сантиметрах
(СГС) (т.е. радианах на метр или радианах
на сантиметр).
Квазиимпульс — векторная величина, характеризующая состояние квазичастицы (например, подвижного электрона в периодическом поле кристаллической решётки). Квазиимпульс частицы связан с её квазиволновым вектором соотношением
Дисперсное соотношение связывающее некоторые величины, характеризующие рассеяние частиц, с величинами, характеризующими их поглощение.