Вопрос 6.

Типы кристаллических решеток. Решетки Бравею вывод формул для постоянной кубической решетки.

Типы кристаллических решеток:

1. Ионная (координационная)

2. Молекулярная (преобладает сила Ван-дер-Ваальса)

3. Атомные (ковалентные)

4. С водородной связью

Решетки Браве:

Триклинная 

Моноклинная

Ромбическая  

Тетрагональная

Гексагональная

Кубическая

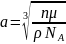
- молярная масса

ρ = плотность при н.у.

n = число одинаковых атомов, приходящихся на элементарную ячейку

= 6,022 [моль^-1 ] - Число Авогадро

Билет 7.

Индексы Миллера для направления и плоскостей в кристаллической решетке. Определение межплоскостных расстояний в кристаллической решетке с помощью дифракции рентгеновских лучей. Формула Брэгга-Вульфа.

Индексы Миллера — кристаллографические индексы, характеризующие расположение атомных плоскостей в кристалле. Индексы Миллера связаны с отрезками, отсекаемыми выбранной плоскостью на трёх осях кристаллографической системы координат (не обязательно декартовой). Таким образом, возможны три варианта относительного расположения осей и плоскости:

• плоскость пересекает все три оси

• плоскость пересекает две оси, а третьей параллельна

• плоскость пересекает одну ось и параллельна двум другим

Индексы направления прямой, проходящей через начало координат, является индекс первого узла, через которую проходит прямая и обозначается [ m n p ] это индексы плоскости (индексы Миллера).

Используя дифракцию рентгеновских лучей на кристалле можно с помощью формулы, закона Вульфа – Брэгга, определить расстояние D.

Условие Вульфа — Брэгга определяет направление максимумов дифракции упруго рассеянного на кристалле рентгеновского излучения. Имеет вид:

;

где d — межплоскостное расстояние, θ — угол скольжения (брэгговский угол), n — порядок дифракционного максимума, λ — длина волны.

Вопрос 8.

Виды связей в кристаллах, зависимость типа решетки от вида связи. Кристаллические решетки с плотной упаковкой атомов.

Кристалли́ческая решётка — пространственное периодическое расположение атомов или ионов в кристалле. Для описания кристаллической решётки достаточно знать расположение частиц в элементарной ячейке кристалла, повторением которой образуется вся кристаллическая решётка.

Виды связей:

1. Связь Ван-дер Вальса (играет роль взаимодействия атомов и молекул) Молекулярные решетки

2. Ионные связи (типичная связь в химических соединениях)

3. Валентные (ковалентная связь) Атомные решетки

4. Металлическая связь присуще для всех металлов

5. Водородная связь (Решетки с водородной связью)

В реальных решетках может присутствовать две и более связи но одна из них является основной.

Билет 9.

Виды дефектов в кристалле. Образование дефектов по Шаттке и по Френкелю, равновесная концентрация дифектов. Влияние точечных дефектов на механические и электрические свойства кристаллов.

Различают точечные дефекты, линейные, поверхностные и объемные.

По Шатке происходит полное испарение атома с поверхности с образованием вакансии. Происходит частичное испарение, т.е. атом переходит в состояние над поверхностью.

По Френкелю происходит диффузия дислокационного атома в другое междоузлие ( возникает вакансия).

Если имеется у нас n вакансия значит равновесная концентрация при температуре T и наличие N узлов равна

Влияние точечных дефектов на механические и электрические свойства кристаллов.

При точечных дефектах атомы примесей вызывают искажение кристаллов решетки.

Энергия образования вакансии. Равновесная концентрация вакансий в кристалле.

Энергия образования вакансии возникает в результате нарушения связей в кристаллической решетке при удалении атома из узла.

Равновесная концентрация вакансий:

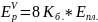
где 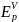 — энергия образования одной вакансии,  — постоянная Больцмана, T — абсолютная температура. Формула показывает, что концентрация вакансий должна сильно зависеть от температуры.

Механизм диффузии по вакансиям. Коэффициент диффузии. Температурная зависимость коэффициента диффузии (уравнение Арениуса). Расчет длины диффузионного пути атома в кристалле.

Для диффузии вакансий и атомов необходимо два условия

1. Около атома должна находится вакансия, для образования которой необходимо энергия  

2. Атом должен обладать энергией для перехода в эту вакансию ( ) .

Коэффицие́нт диффу́зии — количественная характеристика скорости диффузии, равная количеству вещества , проходящего в единицу времени через участок единичной площади при градиенте концентрации, равном единице.

Зависимость коэффициента диффузии от температуры в простейшем случае выражается законом Аррениуса:

,

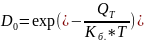где   — коэффициент диффузии [м²/с];   — энергия активации [Дж];   — универсальная газовая постоянная [Дж/К];   — температура [K].