Влияние помехи на вход и выход системы
Введем в систему на рис.9.1 помеху h(t). Для простоты будем полагать, что возмущение отсутствует (M=0).
μ
Рис. 9.2 Система с реальным дифференцирующим фильтром (с помехой)
Запишем уравнение для выхода.
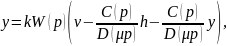
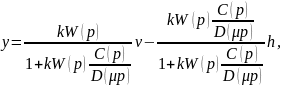
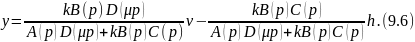
В области рабочих частот из выражения (9.6) имеем обычные соотношения.
Рассмотрим выражение (9.6) в области ВЧ (μp≈1). Тогда при an=bn=c(n-m)=1 уравнение (9.6) вырождается в следующее:
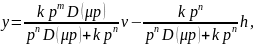
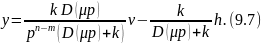
В
статике из уравнения (9.7) видно, что
помеха проходит на выход полностью, так
как
.
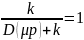В динамике сверхвысокая помеха не
пройдёт, так как старший член
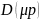будет доминировать, и дробь
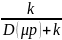будет мала.
Характеристическое уравнение системы на высоких частотах имеет вид
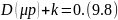
В рабочем диапазоне частот это не проявляется, но на ВЧ характеристическое уравнение (9.8) может дать неустойчивость. В таком случае нужно рассматривать задачу стабилизации системы на быстрых движениях (на ВЧ) по характеристическому уравнению (9.8).
Влияние помех на значение управляющего воздействия
Запишем уравнение по управлению для системы на рис. 9.2.
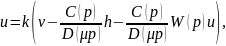
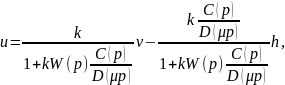
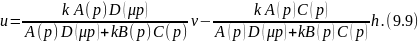
В области низких частот из выражения (9.9) имеем обычные соотношения.
Рассмотрим
выражение (9.9) на высоких частотах:
,
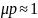где p≈10.
Тогда (9.9) преобразовывается в
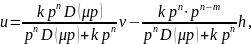
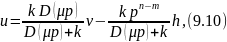
где
- фильтрующий полином.
На
любых частотах в уравнении (9.10)
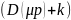и
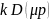дают соизмеримые величины. Помеха
давится фильтрующим полиномом, но
усиливается при помощи дифференцирования
(полином
).
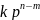μ
Рис. 9.3 ПФ составляющей помехи в управлении
В таком случае используются следующие рекомендации:
На
рабочих частотах
,
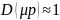следовательно, ПФ на рис. 9.3 вырождается
в
.
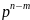На сверхвысоких частотах
)
имеем
.
Тогда ПФ на рис. 9.3 вырождается в
.
Рис. 9.4 ПФ составляющей помехи на сверхвысоких частотах
Для того чтобы сверхвысокочастотная помеха не проходила на управление, порядок дифференцирующего полинома f должен быть больше порядка полинома С(р):
10. Порядок проектирования одноканальных систем с большими коэффициентами
1) Постановка задачи и выбор датчика выходной величины. Датчик выбирается по условию точности исходя из соотношения: погрешность датчика должна быть на порядок меньше допустимой ошибки системы.
2) Разработка математической модели объекта автоматического управления. Для этого нужно разбить структурную схему объекта на типовые элементы; для каждого из элементов написать физические законы, по которым они работают; по конструктивным данным объекта вычислить параметры. После необходимо преобразовать систему уравнений к типовому виду (в идеале – к ПФ). Если не хватает конструктивных данных, проводится идентификация.
3)
Выбор эталонной динамики, то есть
задание полинома С(р)
порядка (n-m).
Исходя из требований к быстродействию
и демпфированию, нужно задать корни и
сформировать полином по формуле
,
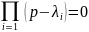а затем привести последний коэффициент
полученного полинома к 1.
4) Выбор коэффициента усиления k. Если объект нормировать (Т=1), то k выбирается от 10 до 15.
5) Выбор дифференцирующего фильтра и его реализации. Условие для выбора: порядок фильтрующего полинома должен быть больше, чем необходимый порядок дифференцирования.
6) Стабилизация быстрых движений.
7) Спаять проектированную схему и сдать заказчику.