6.2 Форсирующее звено в обратной связи

Недостатка, связанного с использованием форсирующего звена в прямом канале, можно избежать, если включить это звено в обратную связь.

Рассмотрим работу системы с форсирующим звеном в ОС.

Рис. 6.2 Структурная схема системы с форсирующим звеном в обратной связи

Запишем уравнение для выхода

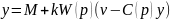
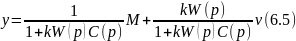
Так как в уравнении (6.5) за счет k 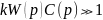, выражение для выхода вырождается в выражение 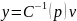. Таким образом, подавляется возмущение М, однако входное воздействие v отрабатывается с инерционным звеном 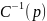порядка (n-m).

Запишем уравнение для управляющего воздействия:

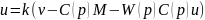
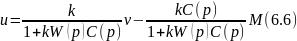
Так как , тогда уравнение для управления (6.6) вырождается в

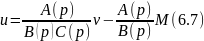
Получаем, что в (6.7) составляющая 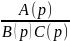не интегрирует и не дифференцирует, следовательно, управление допускает любые изменение входного воздействия v.

Достоинство:

1) Система может отработать скачки входного задающего воздействия v.

Недостаток:

1) Необходимость в форсирующем звене.

7. Устойчивость системы при больших коэффициентах усиления

Передаточная функция для системы на рис. 6.2 имеет следующий вид:

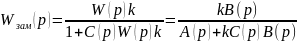
Запишем характеристическое уравнение этой системы.

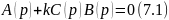
Сделаем несколько предположений для уравнения (7.1).

Предположение 1: .

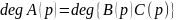Тогда при k→∞ (k может быть как угодно большим) все коэффициенты А(р) будут мало заметны по сравнению с коэффициентами Следовательно, можно коэффициентами А(р) пренебречь . Получим новое характеристическое уравнение:

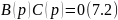
Таким образом, имеем полную независимость свободных свойств системы от параметров объекта (его знаменателя А(р)). Это свойство было ожидаемым, так как было введено форсирующее звено.

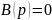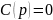Условие устойчивости нового характеристического уравнения (7.2) распадается на два условия: и . Для устойчивости системы с большим коэффициентом требуется устойчивость отдельно полинома В(р) и полинома С(р). Их корни должны быть левыми (с отрицательной вещественной частью). Так как полином С(р) конструируется нами, то он всегда устойчив. Полином В(р) берется из объекта. Следовательно, он может иметь правые корни. В таком случае числитель объекта себя проявит, и замкнутая система станет неустойчивой. Тогда система с большими коэффициентами будет неработоспособной.

Обычная система (без больших коэффициентов) может работать и при правых корнях числителя объекта.

Предположение 2: .

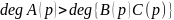Имеем .

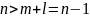Допустим, сэкономили и порядок l выбрали не (n-m), а меньше.

Тогда, пренебрегая членами А(р), получим новое характеристическое уравнение

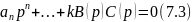
Уравнение (7.3) имеет порядок n. В таком случае, если 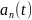зависит от t, то невозможно компенсировать переменные параметры. Если порядок С(р) будет ещё ниже, то большее количество коэффициентов полинома А(р) будут проявляться в динамике системы.

Рассмотрим свойства полинома (7.3) на высоких частотах (р→∞). Тогда в полиноме (7.3) останутся только старшие коэффициенты.

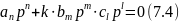
Пусть 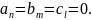Уравнение (7.4) распадается на два уравнение (выносятся нулевые корни):

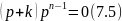
Из уравнения (7.5) имеем корни p₁=0 кратности (n-1) и р₂= -k. Как видим, на высоких частотах преобладает один корень р₂= -k. Таким образом, эта система всегда устойчива (так как k>0) и работоспособна.

Рассмотрим случай, когда порядок C(p) ниже на 1. Следовательно, получим уравнение второго порядка (в нем нет демпфирования, так как система с большим коэффициентом) .

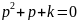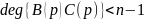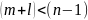Вывод: Если , то есть , то система неработоспособна при больших коэффициентах.

Иначе: Чтобы система была устойчива необходимо ввести инерционность С(р) такого порядка, чтобы порядок 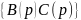был не ниже (n-1).