
- •2. Предельные соотношения
- •3. Метод отрицательной обратной связи
- •4. Интегральный регулятор
- •5. Динамические объекты с большим коэффициентом
- •6. Форсирующий регулятор
- •6.1. Форсирующее звено в прямом канале
- •6.2 Форсирующее звено в обратной связи
- •7. Устойчивость системы при больших коэффициентах усиления
- •8. Реализация форсирующих полиномов (дифференцирующие фильтры)
- •9. Анализ систем с реальным дифференцированием
- •Влияние помехи на вход и выход системы
- •Влияние помех на значение управляющего воздействия
- •10. Порядок проектирования одноканальных систем с большими коэффициентами
- •Нелинейные системы
- •11. Способ отрицательной обратной связи для нелинейного объекта
- •12. Одноканальные канонические системы
- •13. Системы с реальным фильтром
- •14.3 Дифференцирующий фильтр
- •15. Метод малого параметра
- •16. Метод разделения движений
- •17.Разделение движений в системах с большим коэффициентом
Конспект лекций по дисциплине:
«Современные проблемы теории управления
(Проблемы синтеза систем автоматического регулирования)»
ЛИНЕЙНЫЕ СИСТЕМЫ
1. Задача синтеза
Рассмотрим функционально – структурную схему системы регулирования.

Рис. 1.1 Функционально – структурная схема
На рис. 1.1 О – объект управления, М1 – возмущение на объекте, М – возмущение на выходе, h – помеха, v – входное задающее воздействие, u – управляющее воздействие, x – вектор состояния, y – вектор выходных переменных.
Истинное значение у никогда не известно, так как на выход ставится датчик, который измеряет выход с помехами. Таким образом, используется сигнал с датчика.
ν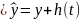
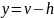
При подборе датчика выходной величины даже при идеальном регуляторе нельзя получить лучше точности, чем обеспечивает датчик.
Задача синтеза состоит в обеспечении следующих требований:
1. Требование к точности.
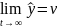
2. Требование к быстродействию.
Предельное быстродействие никогда не нужно из-за высокой стоимости, так как нужен большой всплеск энергии, что в системах не реализуемо.
Т – постоянная времени, характеризующая быстродействие.
3. Требование к демпфированию (колебательности).
Демпфирование определяет запас устойчивости.
Этапы разработки регулятора:
1. Анализ требований к системе
2. По результатам анализа выбирается метод синтеза
3. Регулятор
Пример: ПИД - регулятор: три канала, три настройки, три требования.
Точность – П, И каналы
Быстродействие – П канал
Запас устойчивости – Д канал (этот канал предназначен для стабилизации системы)
Основные: П – регулятор, И – регулятор, ПИ-регулятор.
2. Предельные соотношения
Рассмотрим часть системы регулирования.

Рис. 2.1 Часть системы
Найдем
управляющее воздействие при условии,
что
и управление не должно превышать
допустимого ресурса управляющего
воздействия
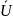 .
.
Запишем выражение для выхода датчика.
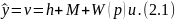
Из уравнения (2.1) выразим управление:
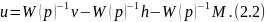
В
(2.2) слагаемое
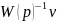 обеспечивает отработку входного
задающего воздействия v.
Следовательно, должно выполняться
условие, что
обеспечивает отработку входного
задающего воздействия v.
Следовательно, должно выполняться
условие, что
 .
Слагаемое
.
Слагаемое
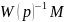 обеспечивает подавление возмущений.
Следовательно,
обеспечивает подавление возмущений.
Следовательно,
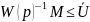 .
Таким образом, ресурса управления должно
хватать на оба слагаемых. Ресурс
управления на помеху рассчитывать не
надо. Она маленькая по абсолютным
значениям, но высокая по частоте. Если
.
Таким образом, ресурса управления должно
хватать на оба слагаемых. Ресурс
управления на помеху рассчитывать не
надо. Она маленькая по абсолютным
значениям, но высокая по частоте. Если
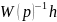 большое, то тракт будет забиваться, и
регулятор не будет справляться. Бороться
с помехой можно при помощи улучшения
качества датчиков и фильтров.
большое, то тракт будет забиваться, и
регулятор не будет справляться. Бороться
с помехой можно при помощи улучшения
качества датчиков и фильтров.
Рассмотрим, какие сигналы можно использовать в качестве эталонного v.
Так
как часть ресурса, требующаяся на
отработку входного воздействия равна
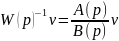 ,
это значит, что ПФ
,
это значит, что ПФ
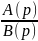 обеспечивает
дифференцирование входного сигнала.
Таким образом, если в качестве v
подавать скачок, то нужен ресурс
управления типа
обеспечивает
дифференцирование входного сигнала.
Таким образом, если в качестве v
подавать скачок, то нужен ресурс
управления типа
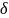 -
функции. Такой ресурс управления
невозможно обеспечить.
-
функции. Такой ресурс управления
невозможно обеспечить.
Вывод:
для того, чтобы система отработала
эталонный сигнал v,
он должен быть «гладким» (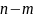 )
раз, то есть дифференцируемым (
)
раз.
)
раз, то есть дифференцируемым (
)
раз.
Возмущение М также должно быть медленно изменяющейся величиной, тогда для его компенсации не потребуется бесконечный ресурс управления.
3. Метод отрицательной обратной связи
1927 г. - Гарольд Стивен Блэк изобрел усилитель с отрицательной обратной связью (ООС).
Рассмотри
простую статическую систему управления
с усилителем с ООС. В качестве регулятора
используется коэффициент усиления
(пропорциональный регулятор). Закон
управления в таком случае имеет вид
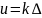 .
.

∆
Рис. 3.1 Схема операционного усилителя с ООС
k
–
коэффициент усиления регулятора, k0(t)
– переменный во времени коэффициент
передачи объекта регулирования, v
– вектор входных переменных, ∆–
ошибка регулирования, u
– вектор управления, M(t)
– переменное во времени возмущение, y
– вектор выходных переменных,
h(t)
– переменная во времени помеха,
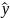 – оценка вектора выходных переменных.
– оценка вектора выходных переменных.
Необходимо обеспечить требование по точности
Вывод выражения для выходной переменной:
 ,
,
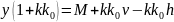 ,
,
 ,
,
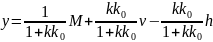 .
.
При
k→∞
имеем,
что
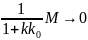 ,
,
 ,
,
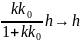 .
.
Таким образом, при достаточно большом значении коэффициента k можно подавить влияние возмущения M, влияние вектора входных переменных v сохраняется, однако, нельзя подавить помеху измерения h. Так же подавляется коэффициент k0(t), который меняется во времени.
Вывод 1: пропорциональный регулятор полностью решает задачу стабилизации нестационарного объекта при действии возмущений.
4. Интегральный регулятор
В
схеме на рис. 3.1 в качестве регулятора
используем интегрирующее звено. Закон
управления в таком случае имеет вид
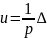 ,
где символ
,
где символ
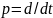 .
Для
простоты примем, что нет помехи измерения
h(t).
.
Для
простоты примем, что нет помехи измерения
h(t).

Рис. 4.1 Схема системы регулирования с И – регулятором
Дифференциальное
уравнение для этой системы относительно
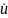 будет иметь следующий вид
будет иметь следующий вид
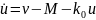 (4.1)
(4.1)
В
точке равновесия (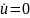 )
имеем:
)
имеем:
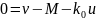
Следовательно,
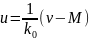 .
(4.2)
.
(4.2)
Таким
образом, из (4.2) при
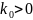 система
выполняет свою задачу (
система
выполняет свою задачу ( ),
а также происходит подавление возмущающего
воздействия М.
),
а также происходит подавление возмущающего
воздействия М.
Вывод 2: интегральный регулятор полностью решает задачу стабилизации нестационарного объекта при действии возмущений.
Достоинства:
1) Нулевая статическая ошибка.
2) В системе нет больших коэффициентов, следовательно, обеспечивается лучшая работа с помехой h(t).
Недостатки:
1) Система стала инерционной (не все объекты допускают наличие инерционности).
2)
Постоянная времени
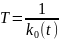 согласно дифференциальному уравнению
(4.1). Таким образом, с течение времени
величина постоянной времени Т
меняется.
согласно дифференциальному уравнению
(4.1). Таким образом, с течение времени
величина постоянной времени Т
меняется.
Наилучшим вариантом буде являться комбинация пропорционального и интегрального регуляторов, а именно ПИ – регулятор.
