Основы статистического анализа-3-к-рус

Занятий по предмету “Основы статистического анализа” 3-курс, специалность «Математика» (рус. гр.)

7-Занятие. Вычисления среднее и дисперсии обединение двух выборки. Вычисления общие, межгруппавые и внутригрупповые дисперсии

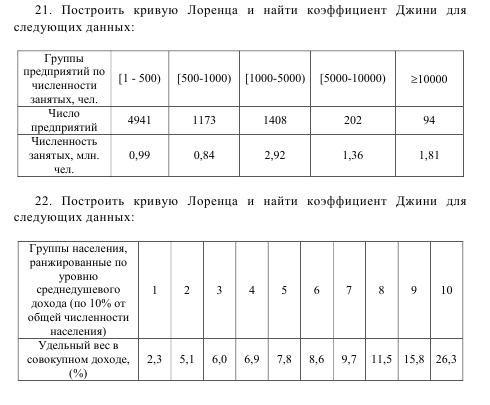
8-Занятие. Кумулятивная сумма. Кривая Лоренца и показатели концентрации.

`

9- Занятие. Построение нармального линий на основе экспериментальных данных. Асимметрия и эксесс.

10- Занятие. Понятие об корреляционной связи. Корреляционная таблица

11- Занятие. Обработка резултатов наблюдений по методу наименьших квадратов. Двумерные выборки

12- Занятие. Геометрическое представление двумерной выборки. Диаграмма рассеяния.

13- Занятие. Коэффициент корреляции-числовая характеристика двумерной выборки.

14- Занятие. Метод наменьших квадратов. Уравнение линейной регрессии

15- Занятие. Другие уравнении регрессии.

16- Занятие. Другие уравнении регрессии.

17- Занятие. Расчет коэффициентов регрессии по сгруппированным данным

Отыскание параметров выборочного уравнения

простой линейной регрессии по сгруппированным данным.

При большом количестве наблюдений одно и то же значение х может встречаться n_x раз, значение у - n_y раз, одна и та же пара может наблюдаться n_xy раз. Поэтому данные наблюдения группируются, т.е. подсчитываются частоты и все данные записывают в виде таблицы, которую, называют корреляционной таблицей. Для данных, заданных в виде корреляционной таблицы, уравнение определяется следующим образом:

Пусть изучается система количественных признаков (X,Y). В результате N независимых опытов получены пары чисел где пара встречается .

Результаты представлены корреляционной таблицей:

X Y			...
			...
			...
...	...	...	...	...	...
			...
			...

Здесь и .

Выборочная ковариация cov(X,Y) величин (X,Y) определяется формулой:

,

где и - выборочные средние признака X и Y.

Выборочные дисперсии:

;

.

Следовательно, выборочный коэффициент корреляции:

.

При отыскание параметров выборочного уравнения простой линейной регрессии по сгруппированным данным, выборочный коэффициент корреляции и коэффициенты уравнения могут быть вычислены непосредственным применением формул.

,

, .

Для оценки качества подбора линейной функции рассчитывается квадрат выборочного коэффициента корреляции , называемый коэффициентом детерминации. Он характеризует долю дисперсии результативного признака у, объясняемую регрессией, в общей доле регрессии. Соответственно величина характеризует долю дисперсии у, вызванную влиянием остальных неучтенных в модели факторов.

Пример 2. Найти выборочное уравнение линейной регрессии Y на Х по данным корреляционной таблицы.

X Y	5	15	25	35	45	55	65	ny
4	2	-	2	-	-	-	-	4
8	-	1	4	-	-	-	-	5
12	-	4	3	10	-	-	-	17
16	-	2	-	2	3	6	-	13
20	-	-	-	-	5	4	-	9
24	-	-	-	-	-	1	1	2
nx	2	7	9	12	8	11	1	N=50

Решение: Вычислим значения следующих сумм:

.

.

.

Найдем выборочный коэффициент корреляции:

Далее найдем коэффициенты уравнения регрессии:

, .

Итак, уравнение регрессии имеет вид: .

Для этого примера =0,5867, следовательно, уравнением регрессии объясняется 58,67% дисперсии результативного признака у, а на долю прочих факторов приходится 41,33% ее дисперсии.

Ответ:

Задания для закрепления:

1. Найти выборочные уравнения линейной регрессии Y на Х и линейной регрессии Х на Y по данным корреляционной таблицы.

X Y	5	10	15	20	25	30	35	40	ny
100	2	1	-	-	-	-	-	-	3
120	3	4	3	-	-	-	-	-	8
140	-	-	5	10	8	-	-	-	23
160	-	-	-	1	-	6	1	1	9
180	-	-	-	-	-	-	4	1	5
nx	5	5	8	11	8	6	5	2	N=50

Ответ: ;

2. Найти выборочные уравнения линейной регрессии Y на Х и линейной регрессии Х на Y по данным корреляционной таблицы.

X Y	18	23	28	33	38	43	48	ny
125	-	1	-	-	-	-	-	1
150	1	2	5	-	-	-	-	8
175	-	3	2	12	-	-	-	17
200	-	-	1	8	7	-	-	16
225	-	-	-	-	3	3	-	6
250	-	-	-	-	-	1	1	2
nx	1	6	8	20	10	4	1	N=50