22.Кратні інтеграли та їх застосування

Означення подвійного інтеграла циліндричний координата

Нехай функція визначена в обмеженій замкнутій області площини . Розіб’ємо область довільним чином на 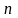елементарних областей, площі котрих, як і самі області, позначатимемо 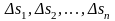. У кожній елементарній області виберемо довільну точку .

Подвійним інтегралом від функції по області називається границя інтегральної суми (1) за умови, що найбільший із діаметрів , прямує до нуля:

.

Подвійний інтеграл позначають так:

.

Означення потрійного інтеграла

Нехай функція визначена в замкненій обмеженій області 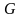тривимірного простору . Розіб’ємо область на довільних частинних областей , які не мають спільних внутрішніх точок. Об’єми областей позначимо позначимо , їх діаметри - . Діаметром області називається довжина найбільшої хорди, яка з’єднує дві точки межі області . Візьмемо довільну точку , і знайдемо значення функції у точці .

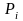Вираз вигляду називається інтегральною сумою для функції по області . Позначимо через максимальний із діаметрів областей , тобто , .

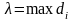Якщо існує границя інтегральної суми за умови, щ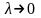о , тобто , яка не залежить від способу розбиття області а елементарні області та від вибору точок , то ця границя називається потрійним інтегралом від функції по області . Потрійний інтеграл позначається так:

.

Застосовується у механіці та фізиці .Наприклад у задачах вимірювання маси,обчислення статичних моментів,моменту інерції

23.Криволінійні інтеграли та їх застосування Криволінійний інтеграл і роду

Нехай на площині Oxy задана неперервна крива AB довжини l. Роздивимось неперервну функцію f(x;y), задану в точках дуги AB. Розіб'ємо криву AB точками M₀=A, M₁, M₂,…, M_n=B на n довільних дуг M_i-1M_i з довжинами відповідно Δl_i (i=1; 2;…; n). Виберемо на кожній дузі M_i-1M_i довільну точку (x_i; y_i) і складемо суму

.

Її називають інтегральною сумою для функції f(x;y) по кривій AB.

Нехай   — найбільша із довжин дуг поділу. Якщо   ( ) існує скінченна границя інтегральних сум, то її називають криволінійним інтегралом від функції f(x;y) по довжині кривої AB, або криволінійним інтегралом І роду від функції f(x;y) по кривій AB і позначають

 або  .

Таким чином, за означенням

.

Криволінійний інтеграл іі роду

Нехай на площині Oxy задана неперервна крива AB довжини і функція P(x;y), визначена в кожній точці кривої. Розіб'ємо криву AB точками M₀=A, M₁, M₂,…, M_n=B в напрямі від точки A до точки B на n довільних дуг M_i-1M_i з довжинами відповідно Δl_i (i=1; 2;…; n). Виберемо на кожній елементарній дузі M_i-1M_i довільну точку (x_i; y_i) і складемо суму

,

де   — проекція дуги M_i-1M_i на вісь Ox. Таку суму називають інтегральною сумою для функції P(x;y) по змінній x.

Нехай   — найбільша із довжин дуг поділу. Якщо   ( ) і існує скінченна границя інтегральних сум, що не залежить від способу розбиття кривої AB і вибору точок (x_i;y_i), то її називають криволінійним інтегралом по координаті x (або II роду) від функції P(x;y) по кривій AB і позначають

 або  .

Таким чином, за означенням

.

Аналогічно виводиться інтеграл від функції Q(x;y) по координаті y:

,

де   — проекція дуги M_i-1M_i на вісь Oy.

Криволінійний інтеграл ІІ роду в загальному вигляді на площині:

Криволінійний інтеграл ІІ роду по кривій в тривимірному просторі визначається аналогічно:

Застосовують в геометрії та механіці.