14.Частинні похідні 1-го порядку функції кількох змінних.Необхідна і достатня умова диференційованості функції двох змінних.

Крім повного приросту ФДЗ

,

існують частинні прирости:

,

.

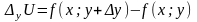Означення. Якщо існує границя відношення частинного приросту ФДЗ до приросту відповідного аргументу, коли останній прямує до нуля, то його називають частинною похідною й позначають:

,

.

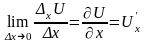Зауваження. Частинну похідну обчислюють як похідну функції однієї змінної за умови, що y зафіксовано, аналогічно для ­- x зафіксовано.

15.Локальні екстремуми функцій двох змінних.Дослідження функцій двох змінних на екстремум.

Локальні екстремуми функції двох змінних

Нехай функція z = f(х, у) визначена в області D, а точка  D. Якщо існує окіл точки  , який належить області D і для всіх відмінних від  точок М цього околу виконується нерівність f (М)< f ( )(f (М) > f ( )), то точку  називають точкою ло­кального максимуму (мінімуму) функції  , а число  – ло­кальним максимумом (мінімумом) цієї функції.

Точки максимуму та мінімуму функції називають її точками екстремуму.

Необхідна ознака існування екстремуму

Якщо функція набуває у точці свого екстремального значення, то в точці або дорівнюють нулю, або нескінченності, або не існують.

Доведення

Крива - лінія перетину поверхні й площини , тоді задана рівнянням Аналогічно доводиться, що й ін. випадки.

Достатня ознака існування екстремуму

Теорема. Нехай у 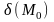функція має неперервні частинні похідні до 3-го порядку включно і точка є стаціонарною, тоді:

1. при 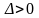є екстремум, якщо , то в точці , якщо ,то в точці ;

2. при 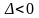- екстремуму немає ;

3. при - потрібні додаткові дослідження.

Тут

16.Первісна і невизначений інтеграл.Основні властивості невизначеного інтегралу.

Означення. Функція 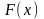називається первісною для функції на проміжку Х, якщо для кожної точки цієї множини виконується рівність

Зауваження. Множина Х є загальною частиною ОДЗ функцій і

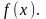
Ясно, що Ф(х) = + c так само є первісною для функції .

Означення. Множина первісних Ф(х) на Х називається інтегралом від функції f(x) по dx і позначається

.

Основні властивості:

1. .

Доведення.

і .

2. або

Доведення

.

3. , де

Доведення: .

17.Інтегрування частинами.Інтегрування методом заміни змінною

Теорема

,

,

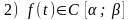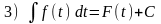, тоді

.

Доведення

.

За формулою Ньютона - Лейбніца

Таким чином, у визначеному інтегралі теж можна провести заміну змінних за правилом

= .

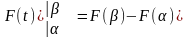Зауваження. Щоб уникнути помилок при заміні змінної у визначеному інтегралі, краще використовувати функції із взаємно однозначною відповідністю множин 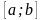і .

Теорема

.

Доведення

,

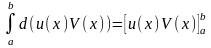, що й треба було довести.

18.Інтегрування раціональних дробів і тригонометричних функцій

Інтегрування найпростіших раціональних дробів

1) , тут А, а  const;

2) ;

3)

;

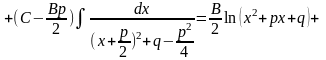
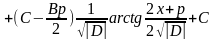4) +

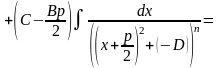
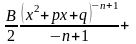
, тут .

Інтегрування тригонометричних функцій

– раціональна функція своїх аргументів, , .

Розглянемо інтеграл від суперпозиції функцій (*).

За допомогою деяких тригонометричних підстановок інтеграл (*) зводиться до інтеграла від дробово-раціональної функції.

1. Універсальна тригонометрична підстановка

,

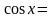
, x =2 arctg t і ,

.

2. Якщо , то можна використовувати підстановку ,

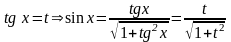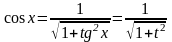, x = arctg t і ,

3. При обчисленні зручно, якщо , зробити підстановку cos x= t, а якщо то sin x = t.