37. Опыт Франка и Герца.

Идея опыта заключалась в доказательстве наличия

с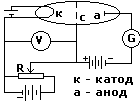 тационарных состояний атоме. 3-электродная

лампа (с - сетка) заполнялась парами ртути с

ρ≈1мм рт. ст. Между катодом и сеткой

прикладывалась ускоряющая разность потенциалов,

которую можно было менять R. Между сеткой и

анодом прикладывалось слабое задерживающее поле.

У станавливалось соотношение между силой тока

между анодом и сеткой и разностью потенциалов

между катодом и сеткой. Согласно идее о наличии

дискретных энергетических уровней у атома при

сталкновении электрона с атомом ртути, атом ртути

воспримет энергию в соотношении, равном

∆E1=E2 – E1, ∆E2=E3 – E2. Т.е. разности энергий 2-х

стационарных состояний. Поэтоу энергия внешних электронов должна уменьшаться в соотношении ∆E1, ∆E2 и т.д. По мере увеличения разности потенциалов, кинетическая энергия электрона растет, и все большее число электронов достигает. проходя через СА; eU=mν2/2. При этих разностях потенциалов Ek<∆E1. При достижении U1=4,9В, Ek равна или чуть больше E1(Ek>=∆E1). В этом случае при столкновении электрона с атомом ртути происходит упругий удар между электроном и атомом ртути, в результате которого электрон отдает часть своей энергии атому ртути. Кинетическая энергия электрона уменьшается и задержанные полем электроны возвращаются в катод. Второй максимум на вольт-амперной характеристики U=9,8В соответствует случаю, когда электрон при столкновении с атомом ртути претерпел 2 неупругих столкновения, при каждом из которых он потерял энергию ∆E1. 3-й максимум – 3 столкновения. Т.о. результаты опыта доказывали наличие у атомов дискретных энергетических состояний.

38. Гипотеза де-Бройля. Соотношение неопределенности.

Гипотеза де Бройля заключалась в том, что электрон, корпускулярные свойства которого (заряд, масса) изучаются давно, имеет еще и волновые свойства, т.е. при определенных условиях ведет себя как волна.

Количественные соотношения, связывающие корпускулярные и волновые свойства частиц, такие же, как для фотонов.

Идея де Бройля состояла в том, что это соотношение имеет универсальный характер, справедливый для любых волновых процессов. Любой частице, обладающей импульсом р, соответствует волна, длина которой вычисляется по формуле де Бройля.

 - волна де Бройля

p =mv- импульс частицы, h - постоянная Планка.

Волны де Бройля, которые иногда называют электронными волнами, не являются электромагнитными.

Свойства волн де Бройля

Пусть частица массы m движется со скоростью v. Тогда фазовая скорость волн де Бройля

.

Т.к. c > v, то фазовая скорость волн де Бройля больше скорости света в вакууме ( v_ф может быть больше и может бытьменше с, в отличие от групповой ).

Групповая скорость

следовательно, групповая скорость волн де Бройля равна скорости движения частицы.

Для фотона

т.е. групповая скорость равная скорости света.

Волны де Бройля испытывают дисперсию. Подставив   в   получим, что v_ф= f(λ). Из-за наличия дисперсии волны де Бройля нельзя представить в виде волнового пакета, т.к. он мгновенно “ расплывется “ (исчезнет) за время 10^-26с.

 Соотношение неопределенностей

 Микрочастицы в одних случаях проявляют себя как волны, в других как корпускулы. К ним не применимы законы классической физики частиц и волн. В квантовой физике доказывается, что к микрочастице нельзя применять понятие траектории, но можно сказать, что частица находится в данном объеме пространства с некоторой вероятностью Р. Уменьшая объем, мы будем уменьшать вероятность обнаружить частицу в нем. Вероятностное описание траектории (или положения) частицы приводит к тому, что импульс и, следовательно, скорость частицы может быть определена с какой-то определенной точностью.

            Далее, нельзя говорить о длине волны в данной точке пространства и отсюда следует, что если мы точно задаем координату Х, то мы ничего не сможем сказать о импульсе частицы, т.к.  . Только рассматривая протяженный участок  мы сможем определить импульс частицы. Чем больше , тем точнее р и наоборот, чем меньше , тем больше неопределенность в нахождении р.

            Соотношение неопределенностей Гейзенберга устанавливает границу в одновременном определении точностиканонически сопряженных величин, к которым относятся координата и импульс, энергия и время.

            Соотношение неопределенностей Гейзенберга: произведение неопределенностей значений двух сопряженных величин не может быть по порядку величины меньше постоянной Планка h

( иногда записывают       )

Таким образом. для микрочастицы не существует состояний, в которых её координата и импульс имели бы одновременно точные значения. Чем меньше неопределенность одной величины, тем больше неопределенность другой.

            Соотношение неопределенностей является квантовым ограничением применимости классической механики к микрообъектам.

следовательно, чем больше m, тем меньше неопределенности в определении координаты и скорости. При m = 10^-12 кг, ?= 10^-6 и Δx = 1% ?, Δv = 6,62·10^-14 м/с, т.е. не будет сказываться при всех скоростях, с которыми пылинки могут двигаться, т.е. для макротел их волновые свойства не играют никакой роли.

            Пусть электрон движется в атоме водорода. Допустим Δx ^-10 м (порядка размеров атома, т.е. электрон принадлежит данному атому). Тогда

Δv = 7,27·^ м/с. По классической механике при движении по радиусу r  ,·^ м v = 2,3·10^-6 м/с. Т.е. неопределенность скорости на порядок больше величины скорости, следовательно, нельзя применять законы классической механики к микромиру.

            Из соотношения   следует, что система имеющая время жизни t, не может быть охарактеризована определенным значением энергии. Разброс энергии   возрастает с уменьшением среднего времени жизни. Следовательно, частота излученного фотона также должна иметь неопределенность  = h, т.е. спектральные линии будут иметь некоторую ширину h, будут размыты. Измерив ширину спектральной линии можно оценить порядок времени существования атома в возбужденном состоянии.