15. Расчёт прочности изгибаемого элемента по нормальному сечению с одиночной арматурой
1. Определяем:
Mf – момент, возникающий в полке двутавра.
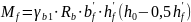
Mtot – момент от полной расчётной нагрузки
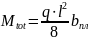
2. Определяем ПРЕДВАРИТЕЛЬНОЕ расположение нейтральной зоны (НЗ):
Мf ≥ Mtot в полке двутавра – сечение рассчитывается как прямоугольное шириной bf
Мf ≤ Mtot в ребре – сечение рассчитывается как двутавровое.
3. Определяем коэффициент αm
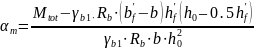
4. Проверяем расположение НЗ:
4.1. Определяем относительную высоту сжатой зоны бетона ξ
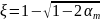
4.2. Определяем
ПРЕДВАРИТЕЛЬНУЮ высоту сжатой зоны
бетона x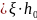
4.3. Проверяем расположение нз
x ≤ h’f НЗ проходит в полке сечения.
x ≥ h’f НЗ проходит в ребре сечения.
4.4. При необходимости пересчитываем αm
ПРИМЕЧАНИЕ: Для конструкций с одиночной арматурой (только в растянутой зоне) должно выполняться неравенство αm ≤ αR , где αR – табличный коэффициент.
5. Определяют площадь требуемой арматуры, определяют As
__________________________________________________________________________________________
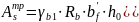
6. С учётом выбранного армирования уточняют высоту сжатой зоны бетона х
6.1. Проверяем расположение НЗ
x ≤ h’f НЗ проходит в полке сечения.
x ≥ h’f НЗ проходит в ребре сечения.
6.2. При необходимости пересчитываем х
7. Определяем предельный изгибающий момент Mult
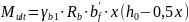
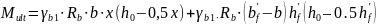
8. Проверяем несущую способность
Mult ≥ Mtot
16. Расчёт прочности изгибаемого элемента по нормальному сечению с двойной арматурой
1. Определяем:
Mf – момент, возникающий в полке двутавра.
Mtot – момент от полной расчётной нагрузки
2. Определяем ПРЕДВАРИТЕЛЬНОЕ расположение нейтральной зоны (НЗ):
Мf ≥ Mtot в полке двутавра – сечение рассчитывается как прямоугольное шириной bf
Мf ≤ Mtot в ребре – сечение рассчитывается как двутавровое.
3. Определяем коэффициент αm
4.1. Определяем граничное значение относительной высоты сжатой зоны бетона ξR по пособию
4.3. Проверяем расположение НЗ
x=h0∙ ξR ≤ h’f НЗ проходит в полке сечения.
x=h0∙ ξR ≥ h’f НЗ проходит в ребре сечения.
4.4. При необходимости пересчитываем αm
ПРИМЕЧАНИЕ: Для конструкций с двойной арматурой (только в растянутой зоне) должно выполняться неравенство αm ≥ αR , где αR – табличный коэффициент.
5. Определяют площадь требуемой арматуры в сжатой зоне, определяют A’s
6. Определяют площадь требуемой арматуры в растянутой зоне, определяют As
__________________________________________________________________________________________
7. Определяют положение границы сжатой зоны бетона
- НЗ
проходит в полке сечения.
- НЗ
проходит в ребре сечения.
8. С учётом выбранного армирования уточняют высоту сжатой зоны бетона х
8.1. Проверяем расположение НЗ
ξ ≤ ξR НЗ проходит в полке сечения.
ξ ≥ ξR НЗ проходит в ребре сечения.
ξ = x/h0
8.2. При необходимости пересчитываем х
9. Определяем предельный изгибающий момент Mult
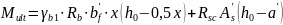
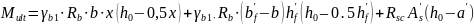
10. Проверяем несущую способность Mult ≥ Mtot