2.1.2 Расчет минимального радиуса поворота гусеничной машины

Минимальный радиус поворота гусеничной машины реализуется при развороте машины на месте, при этом тяга на забегающей гусенице равна тяге на отстающей гусенице и противоположна по направлению.

Таким образом, минимальный радиус гусеничной машины будет определяться шириной колеи машины.

, (2.2)

2.1.3 Расчет теоретических радиусов поворота гусеничной машины

Для определения баланса мощности гусеничной машины в повороте необходимо разбить диапазон возможных радиусов поворота гусеничной машины на несколько частей, определив 5 контрольных точек возможных радиусов поворота.

В дальнейшем при расчетах будем определять значения показателей для каждой из 5 расчетных точек.

2.2 Расчет динамических характеристик поворота гусеничной машины

2.2.1 Определение коэффициента сопротивления повороту

Для каждого выбранного значения радиусов поворота рассчитывается коэффициент сопротивления повороту по формуле

, (2.3)

^где – ^{выбранное значение радиуса поворота.}

2.2.2 Определение удельной силы тяги на забегающей гусенице

Удельная сила тяги рассчитывается по уравнению

, (2.4)

где f_гр – сопротивление прямолинейному движению, принимается по таблице 1 Приложения 3.

2.2.3 Расчет удельной силы на отстающей гусенице

Удельная сила на отстающей гусенице рассчитывается по уравнению

(2.5)

2.2.4 Расчет удельной силы тяги, потребной для поворота с «идеальным» механизмом поворота

Удельная сила тяги, потребная для поворота гусеничной машины с «идеальным» механизмом поворота, рассчитывается по уравнению

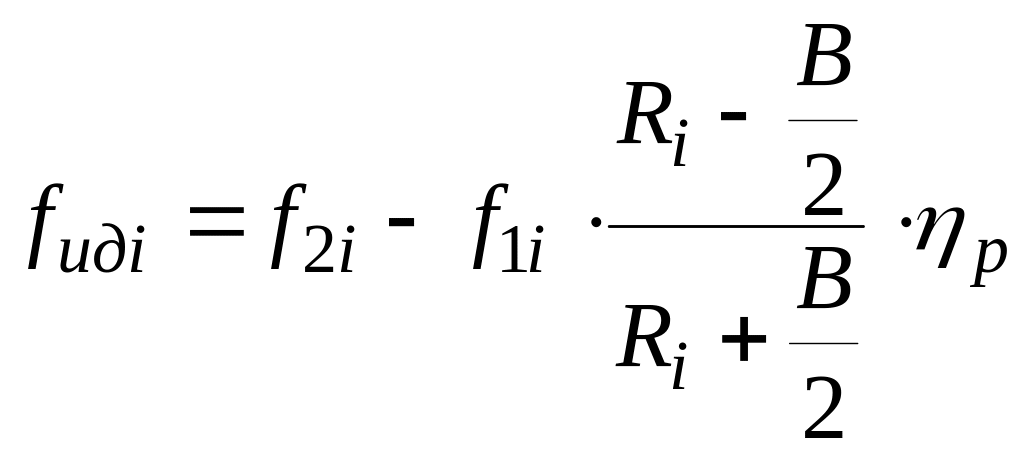, (2.6)

где – КПД контура рекуперации;

– КПД гусеничного движителя на заданной скорости;

– КПД бортовой передачи гусеничной машины;

– КПД механизма поворота гусеничной машины;

Из анализа исходных данных следует, что η_гд является неизвестным. Для

его определения используется эмпирическая формула:

, (2.7)

где a, b, c – эмпирические коэффициенты.

Скорость V_max в приведённом уравнении подставляется в км/ч. Для выполнения расчетов в курсовом проекте скорость принимается 50% от максимальной скорости гусеничной машины, указанной в задании.

2.2.6 Расчет удельной силы внешних сопротивлений повороту

Удельная сила внешних сопротивлений повороту гусеничной машины с механизмом поворота второго типа определяется уравнением

, (2.8)

где – КПД гусеничной машины;

– КПД трансмиссии.

Данные расчета баланса мощности при повороте гусеничной машины сводятся в таблице 2.1.

По результатам таблицы 2.1 строится трафик баланса удельных сил при повороте гусеничной машины (рисунок 2.l).

Таблица 2.1 - Данные расчета баланса мощности при повороте гусеничной машины

Параметры поворота	Условные обозначения	Радиусы поворота
		R1=В/2	R2	R3	R4	R5=Rсв
Коэффициент сопротивления повороту	μ
Удельная сила тяги на забегающей гусенице	f2
Удельная сила тяги на отстающей гусенице	f1
Удельная сила тяги для поворота машины с «идеальным» МП	fuд
Удельная сила внешних сопротивлений повороту	fo

Для получения величины мощности, требуемой для поворота машины на i-ом радиусе, необходимо соответствующую удельную силу умножить на постоянный коэффициент .

Рисунок 2.1 – Баланс мощности поворота гусеничной машины с идеальным механизмом поворота II типа