1)Взаимодействие зарядов. Закон сохранения электрического заряда. Системы единиц
Известно, что одноименные заряды отталкиваются, разноименные - притягиваются. Закон взаимодействия зарядов впервые сформулировал Кулон в 1785 г. (закон Кулона): |
|
q1, q2 - взаимодействующие заряды, r - расстояние между зарядами.
Сила направлена вдоль прямой, соединяющей заряды. В векторном виде закон Кулона: |
|
1/4П ε0=к
ε0= 8.85*10-12 Ф/м
ЗСЗ
Зако́н сохране́ния электри́ческого заря́да гласит, что алгебраическая сумма зарядов электрически замкнутой системы сохраняется.
![]()
Система единиц Заряд измеряется в Кл 1Кл = 1А*1с Элементарный заряд е=1.6*10-19 Кл
2) Напряженность и потенциал электрического поля

Напряженность электрического поля характеризуется силой, которая действует на точечный электрический заряд, помещенный в это поле.
Потенциал электрического поля
Электростатический потенциа́л (см. также кулоновский потенциал) — скалярная энергетическая характеристика электростатического поля, характеризующая потенциальную энергию, которой обладает единичный положительный пробный заряд, помещённый в данную точку поля. Единицей измерения потенциала в Международной системе единиц (СИ) является вольт (русское обозначение: В; международное: V), 1 В = 1 Дж/Кл
Электростатический потенциал равен отношению потенциальной энергии взаимодействия заряда с полем к величине этого заряда:
![]() Wp=qφ
Wp=qφ

3) Силовые линии и эквипотенциальные поверхности
Силовые линии указывают направление силы, действующей на положительный заряд в данной точке поля.
Свойства силовых линий электрического поля
Силовые линии электрического поля имеют начало и конец. Они начинаются на положительных зарядах и заканчиваются на отрицательных.
Силовые линии электрического поля всегда перпендикулярны поверхности проводника.
Распределение силовых линий электрического поля определяет характер поля. Поле может быть радиальным (если силовые линии выходят из одной точки или сходятся в одной точке), однородным (если силовые линии параллельны) и неоднородным (если силовые линии не параллельны).
Эквипотенциальные поверхности — понятие, применимое к любому потенциальному векторному полю, например, к статическому электрическому полю или к ньютоновскому гравитационному полю. Эквипотенциальная поверхность — это поверхность, на которой скалярный потенциал данного потенциального поля принимает постоянное значение (поверхность уровня потенциала). Другое, эквивалентное, определение — поверхность, в любой своей точке ортогональная силовым линиям поля.
Поверхность проводника в электростатике является эквипотенциальной поверхностью. Кроме того, помещение проводника на эквипотенциальную поверхность не вызывает изменения конфигурации электростатического поля. Этот факт используется в методе изображений, который позволяет рассчитывать электростатическое поле для сложных конфигураций.
4) Связь напряженности и потенциала электрического поля
E-напряженность электрического поля
ф-потенциал
E = -grad ф
5) Напряженность и потенциал от электрического диполя.
Два равных по величине и противоположных по знаку точечных заряда Q, находящиеся на расстоянии r друг от друга, называются электрическим диполем.
E0=Eε


6) Электрический диполь во внешнем поле.
2.2. Электрический диполь во внешнем электрическом поле
Рассмотрим,
каким воздействиям подвергается
электрический диполь с электрическим
моментом ![]() во
внешнем электростатическом поле
во
внешнем электростатическом поле ![]() .
В этих условиях он испытывает действие
силы
.
В этих условиях он испытывает действие
силы
|
(2.8) |
момента
|
(2.9) |
и приобретает потенциальную энергию
|
(2.10) |
В процессе вывода соотношений (2.8) - (2.10) станет ясен математический и физический смысл приведенных выражений.
Перед началом выкладок напомним некоторые сведения из математического анализа. Для скалярной функции одного переменного справедливо приближенное выражение
|
(2.11) |
Это соотношение легко обобщается для случая скалярной функции нескольких пространственных переменных:
|
(2.12) |
Если ![]() -радиус-вектор
произвольной точки пространства,
-радиус-вектор
произвольной точки пространства, ![]() -
малый произвольный вектор с компонентами
-
малый произвольный вектор с компонентами ![]() ,
то выше приведенное выражение можно
записать в форме:
,
то выше приведенное выражение можно
записать в форме:
![]()
![]() ,
,
|
(2.13) |
формально
|
(2.14) |
причем соотношение (2.14) справедливо в декартовой системе координат.
Для
векторной величины ![]() соотношение (2.13) можно
записать для каждой компоненты отдельно,
а в компактной форме записи получить:
соотношение (2.13) можно
записать для каждой компоненты отдельно,
а в компактной форме записи получить:
![]()
|
(2.15) |
Зависимости (2.13) и (2.15) являются обобщением отрезка ряда Тейлора для скалярной функции одного переменного (2.11) на многомерный случай скалярного и векторного полей.
|
Рис. 2.3. Электрический диполь во внешнем электростатическом поле |
Рассчитаем
силу, действующую на электрический
диполь во внешнем электростатическом
поле ![]() (рис.
2.3). На рис 2.3
-
радиус-вектор точки расположения
отрицательного заряда диполя, а
(рис.
2.3). На рис 2.3
-
радиус-вектор точки расположения
отрицательного заряда диполя, а ![]() -
радиус-вектор точки расположения
положительного заряда диполя. Суммарная
сила, действующая на рассматриваемую
систему электрических зарядов описывается
выражением:
-
радиус-вектор точки расположения
положительного заряда диполя. Суммарная
сила, действующая на рассматриваемую
систему электрических зарядов описывается
выражением:
![]() .
.
|
(2.16) |
С учетом приведенного выше соотношения (2.15) получим
![]() .
.
Результат (2.8) получен.
Заметим, что зависимость (2.8) в
случае однородного электрического
поля ![]() обращается
в нуль.
обращается
в нуль.
Для момента сил, действующих на рассматриваемую систему электрических зарядов, относительно начала координат имеем:
|
(2.17) |
Если
в выражении (2.17) использовать
соотношение (2.15) для
вычисления ![]() и
в полученном соотношении пренебречь
членом с сомножителем
и
в полученном соотношении пренебречь
членом с сомножителем ![]() из-за
его малости, приходим к результату:
из-за
его малости, приходим к результату:
|
(2.18) |
где
![]() определено
соотношением (2.8).
определено
соотношением (2.8).
|
Рис. 2.4. Момент сил, действующий на электрический диполь во внешнем |
Если
рассчитывать момент сил (2.18) относительно
точки расположения отрицательного
заряда диполя, то получаем ![]() и
приходим к соотношению (2.9).
Тот же результат получается и при расчете
момента сил (2.18)относительно
центра масс системы электрических
зарядов.
и
приходим к соотношению (2.9).
Тот же результат получается и при расчете
момента сил (2.18)относительно
центра масс системы электрических
зарядов.
Рассчитаем величину потенциальной энергии, приобретаемой электрическим диполем во внешнем электрическом поле. Будем исходить из очевидного соотношения:
|
(2.19) |
С помощью формулы (2.13) преобразуем соотношение (2.19):
|
(2.20) |
где ![]() -
угол между вектором
-
угол между вектором ![]() и
направлением напряженности
электростатического поля
и
направлением напряженности
электростатического поля
![]() .
Таким образом, соотношения (2.8) - (2.10) доказаны.
.
Таким образом, соотношения (2.8) - (2.10) доказаны.
|
Рис. 2.5. Потенциальная энергия электрического диполя в однородном электростатическом поле в зависимости от ориентации диполя |
Обсудим
некоторые следствия полученных
результатов. Из формулы (2.8),
в частности, следует, что только в
неоднородном поле ![]() возникает
сила, действующая на диполь как на
систему зарядов. Из формулы (2.20) следует,
что потенциальная энергия системы будет
минимальна, если направления
векторов
и
возникает
сила, действующая на диполь как на
систему зарядов. Из формулы (2.20) следует,
что потенциальная энергия системы будет
минимальна, если направления
векторов
и ![]() совпадают
между собой (
совпадают
между собой (![]() ,
,
![]() ).
В этом состоянии момент сил (2.9) обращается
в ноль.
).
В этом состоянии момент сил (2.9) обращается
в ноль.
|
Рис. 2.6. Сила, действующая на электрический диполь в поле точечного положительного заряда.
|
В целом электростатическое поле
1. стремится развернуть электрический диполь вдоль силовой линии электрического поля;
2.
стремится сдвинуть электрический диполь
вдоль силовой линии векторного поля
в
сторону больших значений величины ![]() ;
;
3. при повороте вектора дипольного момента относительно силовой линии поля возникает "возвращающий" момент сил, в гармоническом приближении пропорциональный углу поворота.
7) Теорема Гаусса для вектора Е.
Теорема Остроградского - Гаусса (закон Гаусса) — один из основных законов электродинамики, входит в систему уравнений Максвелла. Выражает связь (а именно равенство с точностью до постоянного коэффициента) между потоком напряжённости электрического поля сквозь замкнутую поверхность и зарядом в объёме, ограниченном этой поверхностью. Применяется отдельно для вычисления электростатических полей.
Общая формулировка: Поток вектора напряжённости электрического поля через любую произвольно выбранную замкнутую поверхность пропорционален заключённому внутри этой поверхностиэлектрическому заряду.
СГС |
СИ |
|
|
где
 —
поток
вектора напряжённости электрического
поля через замкнутую поверхность
—
поток
вектора напряжённости электрического
поля через замкнутую поверхность  .
. —
полный
заряд, содержащийся в объёме, который
ограничивает поверхность
.
—
полный
заряд, содержащийся в объёме, который
ограничивает поверхность
. — электрическая
постоянная.
— электрическая
постоянная.
Данное выражение представляет собой теорему Гаусса в интегральной форме.
Замечание: поток вектора напряжённости через поверхность не зависит от распределения заряда (расположения зарядов) внутри поверхности.
В дифференциальной форме теорема Гаусса выражается следующим образом:
СГС |
СИ |
|
|
Здесь ![]() —
объёмная плотность заряда (в случае
присутствия среды — суммарная
плотность свободных и связанных зарядов),
а
—
объёмная плотность заряда (в случае
присутствия среды — суммарная
плотность свободных и связанных зарядов),
а ![]() — оператор
набла.
— оператор
набла.
Теорема Гаусса может быть доказана как теорема в электростатике исходя из закона Кулона (см. ниже). Формула однако также верна в электродинамике, хотя в ней она чаще всего не выступает в качестве доказываемой теоремы, а выступает в качестве постулируемого уравнения (в этом смысле и контексте ее логичнее называть законом Гаусса[2].
8) Следствия из теоремы Гаусса для вектора Е ( 3 примера)
9) Проводники в электрическом поле.
Вещество или материальное тело, в котором имеются заряды, способные переносить электрический ток, называется проводником. В металлах переносчиками тока служат свободные (т.е. не привязанные к атомам) электроны, в электролитах — ионы, в плазме — и электроны, и ионы. Для электростатических явлений поле внутри проводника равно нулю:
E→in ≡ 0 .
Механизм исчезновения электрического поля в проводниках связан со смещением свободных зарядов ровно настолько, чтобы как раз компенсировать внешнее электрическое поле, если таковое имеется. При изменении внешнего поля свободные заряды в проводнике перераспределяются, а в момент перераспределения в проводнике течет ток. Пример такой компенсации внутри проводящей пластины изображен на рис. 1.25.

|
Поскольку E→in = 0, то и плотность заряда внутри проводника также равна нулю:
ρin = 1 4π divE→in ≡ 0.
Заряды, компенсирующие внешнее поле, могут размещаться только на поверхности проводника. В связи с этим говорят, что проводник квазинейтрален. По аналогии с объёмной плотностью заряда ρ = limΔV →0Δq∕ΔV , поверхностную плотность определяют, как предел отношения заряда на физически малом участке поверхности Δq к площади этого участка ΔS:
σ = limΔS→0Δq∕ΔS .
Все точки проводника имеют одинаковый потенциал, так как gradϕin = −E→in = 0. Поверхность проводника также эквипотенциальна. Следовательно, электрическое поле перпендикулярно к ней. Этот факт иногда формулируют в виде равенства нулю тангенциальной (касательной к поверхности проводника) проекции внешнего электрического поля E→t = [[n→,E→],n→]:
E→t = 0.
Здесь и далее n→ обозначает внешнюю нормаль к поверхности проводника.
|
Нормальная компонента электрического поля на поверхности проводника En = (n→,E→) однозначно связана с поверхностной плотностью зарядов. Применяя теорему Гаусса к параллелепипеду, натянутому на элемент поверхности проводника (рис. 1.26), получаем:
E→n = 4πσ .
Обычно распределение зарядов σ по поверхности проводника неизвестно. Если нужно, его находят в результате решения задачи (см. след. параграф). Однако одну существенную закономерность можно указать из качественных соображений (Б.Франклин, 1747 г.). Так как одноименные заряды (заряды одного знака) отталкиваются, они стремятся разойтись в проводнике как можно дальше. Это приводит к накоплению зарядов на наиболее удаленных участках проводников, например на остриях. Поле вблизи острия можно приближенно представить, как поле заряженной сферы того же радиуса кривизны r. Отсюда можно оценить напряженность электрического поля и поверхностную плотность заряда 4πσ ∼ E ∼ ϕ∕r, где ϕ — потенциал проводника относительно соседних тел. При этом полезно отметить, что полный заряд острия q ∼ πr2σ ∼ ϕr все-таки составляет малую долю заряда всего проводящего тела Q ∼ ϕR, где R — его характерный размер.
10) Диэлектрики
Диэлектрическими называют материалы, основным электрическим свойством которых является способность к поляризации и в которых возможно существование электростатического поля. Реальный (технический) диэлектрик тем более приближается к идеальному, чем меньше его удельная проводимость и чем слабее у него выражены замедленные механизмы поляризации, связанные с рассеиванием электрической энергии и выделением, теплоты.
При применении диэлектриков — одного из наиболее обширных классов электротехнических материалов — довольно четко определилась необходимость использования как пассивных, так и активных свойств этих материалов.
Пассивные свойства диэлектрических материалов используются, когда их применяют в качестве электроизоляционных материалов и диэлектриков конденсаторов обычных типов. Электроизоляционными материалами называют диэлектрики, которые не допускают утечки электрических зарядов, т.е. с их помощью отделяют электрические цепи друг от друга или токоведущие части устройств, приборов и аппаратов от проводящих, но не токоведущих частей (от корпуса, от земли). В этих случаях диэлектрическая проницаемость материала не играет особой роли или она должна быть возможно меньшей, чтобы не вносить в схемы паразитных емкостей. Если материал используется в качестве диэлектрика конденсатора определенной емкости и наименьших размеров, то при прочих равных условиях желательно, чтобы этот материал имел большую диэлектрическую проницаемость.
Активными (управляемыми) диэлектриками являются сегнетоэлектрики, пьезоэлектрики, пироэлектрики, электролюминофоры, материалы для излучателей и затворов в лазерной технике, электреты и др.
В зависимости от влияния напряженности электрического поля на значение относительной диэлектрической проницаемости материала все диэлектрики подразделяют на линейные и нелинейные.
Для линейных диэлектриков с малыми потерями энергии зависимость заряда конденсатора от напряжения (переменной полярности) имеет вид прямой; для нелинейных диэлектриков (сегнетоэлектриков) в этих условиях зависимость заряда от напряжения принимает форму петли гистерезиса (см. рис. далее).
Неполярными диэлектриками являются газы, жидкости и твердые вещества в кристаллическом и аморфном состояниях, обладающие в основном только электронной поляризацией. К ним относятся водород, бензол, парафин, сера, полиэтилен и др.
Полярные (дипольные) диэлектрики — это органические жидкие, полужидкие и твердые вещества, имеющие одновременно дипольно-релаксационную и электронную поляризации. К ним относятся нитробензол, кремнийорганические соединения, фенолформальдегидные смолы, эпоксидные компаунды, хлорированные углеводороды, капрон и др.
11)Теорема Гауса для вектора D
В диэлектрической среде могут присутствовать электрические заряды двух типов: "свободные" и "связанные". Первые из них не связаны с молекулярной структурой вещества и, как правило, могут относительно свободно перемещаться в пространстве. Вторые связаны с молекулярной структурой вещества и под действием электрического поля могут смещаться из положения равновесия, как правило, на очень малые расстояния.
Использование напрямую теоремы Гаусса для векторного поля при описании диэлектрической среды неудобно тем, что правая часть формулы
|
(2.30) |
содержит
как величину "свободного", так и
величину "связанного"
(некомпенсированного) зарядов внутри
замкнутой поверхности ![]() .
.
Если соотношение (2.30) почленно сложить с соотношением (2.28), получим
|
(2.31) |
где ![]() -
суммарный "свободный" заряд объема,
охватываемого замкнутой поверхность
-
суммарный "свободный" заряд объема,
охватываемого замкнутой поверхность ![]() .
Соотношение (2.31) обуславливает
целесообразность введения специального
вектора
.
Соотношение (2.31) обуславливает
целесообразность введения специального
вектора
|
(2.32) |
в
качестве удобной расчетной величины,
характеризующей электрическое поле в
диэлектрической среде. Вектор ![]() раньше
называли вектором электрической индукции
или вектором электрического смещения.
В настоящее время входит в употребление
термин "вектор
".
раньше
называли вектором электрической индукции
или вектором электрического смещения.
В настоящее время входит в употребление
термин "вектор
".
Для
векторного поля ![]() справедлива
интегральная форма теоремы Гаусса:
справедлива
интегральная форма теоремы Гаусса:
|
(2.33) |
и, соответственно, дифференциальная форма теоремы Гаусса:
|
(2.34) |
где ![]() -
объемная плотность свободных зарядов.
-
объемная плотность свободных зарядов.
Если справедливо соотношение (2.27) (для жестких электретов оно не справедливо), то для вектора из определения (2.32) следует
|
(2.35) |
где ![]() -
диэлектрическая проницаемость среды,
одна из важнейших электрических
характеристик вещества. В электростатике
и квазистационарной электродинамике
величина
-
диэлектрическая проницаемость среды,
одна из важнейших электрических
характеристик вещества. В электростатике
и квазистационарной электродинамике
величина ![]() является
действительной. При рассмотрении
высокочастотных колебательных процессов
фаза колебания вектора
является
действительной. При рассмотрении
высокочастотных колебательных процессов
фаза колебания вектора ![]() ,
а значит и вектора
,
может не совпадать с фазой колебаний
вектора
,
в таких случаях величина
становится
комплекснозначной величиной.
,
а значит и вектора
,
может не совпадать с фазой колебаний
вектора
,
в таких случаях величина
становится
комплекснозначной величиной.
Рассмотрим вопрос, при каких условиях в диэлектрической среде возможно появление некомпенсированной объемной плотности связанных зарядов. Для этой цели запишем выражение вектора поляризации через диэлектрическую проницаемость среды и вектор :
|
(2.36) |
в
справедливости которого легко убедиться.
Теперь представляющая интерес
величина ![]() может
быть вычислена:
может
быть вычислена:
|
(2.37) |
В
отсутствие в диэлектрической среде
объемной плотности свободных
зарядов ![]() величина
величина ![]() может
обратиться в нуль, если
может
обратиться в нуль, если
а) отсутствует поле ;
или
б) среда однородна
![]()
или
в) векторы
и ![]() -
ортогональны.
-
ортогональны.
В общем случае необходимо вычислить величину по соотношениям (2.37).
12)Граничные условия для векторов Е и D
На поверхности раздела двух диэлектриков с различными абсолютными диэлектрическими проницаемостями e1 и e2 (рис. 1.3) равны между собой касательные составляющие напряженности поля
![]()
(1.13)
и нормальные составляющие вектора электрического смещения
![]() (1.14)
(1.14)
Здесь индекс 1 относится к первому диэлектрику, а индекс 2 – ко второму.
Условия (1.13) и (1.14) можно представить и в таком виде
![]() и
и ![]() .
.
Из данных граничных условий можно получить еще одно условие – условие преломления линий поля при переходе их из одного диэлектрика в другой:
![]()
![]() ,
,
где
q1 и q2 – углы между вектором напряженности (или смещения) и нормалями к границе раздела сред.
При этом, если вектор напряженности перпендикулярен к границе раздела, то электрическое смещение не меняется при переходе из одной среды в другую, а напряженность поля меняется скачком.
При переходе через границу раздела двух диэлектриков электрический потенциал не претерпевает скачков.

13) Преломление силовых линий на границе раздела диэлектриков
На границе двух диэлектриков с различными диэлектрическими проницаемостями 1, и 2 при наличии внешнего поля возникают поляризационные заряды разного знака с различными поверхностными плотностями зарядов +1' и +2'.

Из данных граничных условий можно получить еще одно условие – условие преломления линий поля при переходе их из одного диэлектрика
в другой:


где ![]() и
и ![]() –
углы между вектором напряженности (или
плотности тока) и нормалями к границе
раздела сред. При этом, если вектор
напряженности перпендикулярен к границе
раздела, то плотность тока не меняется
при переходе из одной среды в другую, а
напряженность поля меняется скачком.
–
углы между вектором напряженности (или
плотности тока) и нормалями к границе
раздела сред. При этом, если вектор
напряженности перпендикулярен к границе
раздела, то плотность тока не меняется
при переходе из одной среды в другую, а
напряженность поля меняется скачком.
Закон преломления линий тока по форме вполне аналогичен закону преломления линий электрического смещения на границе двух диэлектриков в электростатическом поле.
Во многих практических случаях мы встречаемся с переходом тока из металлических тел в окружающую среду, удельная проводимость которой во много раз меньше удельной проводимости материала этих тел. Такие условия имеют место, например, в случае перехода тока через зарытые в землю металлические электроды. Обычно применяют стальные электроды.
14) Электроемкость
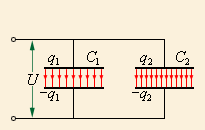
Если двум изолированным друг от друга проводникам сообщить заряды q1 и q2, то между ними возникает некоторая разность потенциалов Δφ, зависящая от величин зарядов и геометрии проводников. Разность потенциалов Δφ между двумя точками в электрическом поле часто называют напряжением и обозначают буквой U. Наибольший практический интерес представляет случай, когда заряды проводников одинаковы по модулю и противоположны по знаку: q1 = – q2 = q. В этом случае можно ввести понятие электрической емкости.
Электроемкостью системы из двух проводников называется физическая величина, определяемая как отношение заряда q одного из проводников к разности потенциалов Δφ между ними:
|
В системе СИ единица электроемкости называется фарад (Ф):
|
Величина электроемкости зависит от формы и размеров проводников и от свойств диэлектрика, разделяющего проводники. Существуют такие конфигурации проводников, при которых электрическое поле оказывается сосредоточенным (локализованным) лишь в некоторой области пространства. Такие системы называются конденсаторами, а проводники, составляющие конденсатор, – обкладками.
Простейший конденсатор – система из двух плоских проводящих пластин, расположенных параллельно друг другу на малом по сравнению с размерами пластин расстоянии и разделенных слоем диэлектрика. Такой конденсатор называется плоским. Электрическое поле плоского конденсатора в основном локализовано между пластинами (рис. 1.6.1); однако, вблизи краев пластин и в окружающем пространстве также возникает сравнительно слабое электрическое поле, которое называют полем рассеяния. В целом ряде задач приближенно можно пренебрегать полем рассеяния и полагать, что электрическое поле плоского конденсатора целиком сосредоточено между его обкладками (рис. 1.6.2). Но в других задачах пренебрежение полем рассеяния может привести к грубым ошибкам, так как при этом нарушается потенциальный характер электрического поля (см. § 1.4).
|
Рисунок 1.6.1. Поле плоского конденсатора |
|
Рисунок 1.6.2. Идеализированное представление поля плоского конденсатора. Такое поле не обладает свойством потенциальности |
Каждая из заряженных пластин плоского конденсатора создает вблизи поверхности электрическое поле, модуль напряженности которого выражается соотношением (см. § 1.3)
|
Согласно
принципу суперпозиции, напряженность ![]() поля,
создаваемого обеими пластинами, равна
сумме напряженностей
поля,
создаваемого обеими пластинами, равна
сумме напряженностей ![]() и
и ![]() полей
каждой из пластин:
полей
каждой из пластин:
|
Внутри конденсатора вектора и параллельны; поэтому модуль напряженности суммарного поля равен
|
Вне пластин вектора и направлены в разные стороны, и поэтому E = 0. Поверхностная плотность σ заряда пластин равна q / S, где q – заряд, а S – площадь каждой пластины. Разность потенциалов Δφ между пластинами в однородном электрическом поле равна Ed, где d – расстояние между пластинами. Из этих соотношений можно получить формулу для электроемкости плоского конденсатора:
|
Таким образом, электроемкость плоского конденсатора прямо пропорциональна площади пластин (обкладок) и обратно пропорциональна расстоянию между ними. Если пространство между обкладками заполнено диэлектриком, электроемкость конденсатора увеличивается в ε раз:
|
Примерами конденсаторов с другой конфигурацией обкладок могут служить сферический и цилиндрический конденсаторы. Сферический конденсатор – это система из двух концентрических проводящих сфер радиусов R1 и R2. Цилиндрический конденсатор – система из двух соосных проводящих цилиндров радиусов R1 и R2 и длины L. Емкости этих конденсаторов, заполненных диэлектриком с диэлектрической проницаемостью ε, выражаются формулами:
|
Конденсаторы могут соединяться между собой, образуя батареи конденсаторов. При параллельном соединении конденсаторов (рис. 1.6.3) напряжения на конденсаторах одинаковы: U1 = U2 = U, а заряды равны q1 = С1U и q2 = C2U. Такую систему можно рассматривать как единый конденсатор электроемкости C, заряженный зарядом q = q1 + q2 при напряжении между обкладками равном U. Отсюда следует
|
Таким образом, при параллельном соединении электроемкости складываются.
|
|
При
последовательном соединении (рис. 1.6.4)
одинаковыми оказываются заряды обоих
конденсаторов: q1 = q2 = q,
а напряжения на них равны  и
и  Такую
систему можно рассматривать как единый
конденсатор, заряженный зарядом q при
напряжении между обкладками U = U1 + U2.
Следовательно,
Такую
систему можно рассматривать как единый
конденсатор, заряженный зарядом q при
напряжении между обкладками U = U1 + U2.
Следовательно,
|
15) Соединение конденсаторов в батареи
|
![]() .
.
С другой стороны,
![]() .
.
Сравнивая эти выражения, получаем:
![]() .
.
Таким образом, при параллельном соединении конденсаторов емкость батареи равна сумме их емкостей.
|
 .
.
С другой стороны,
![]() .
.
Сравнивая эти выражения между собой, получим, что при последовательном соединении складываются величины, обратные емкостям отдельных конденсаторов:
 .
.
16) Энергия электрического поля
Опыт показывает, что заряженный конденсатор содержит запас энергии.
Энергия заряженного конденсатора равна работе внешних сил, которую необходимо затратить, чтобы зарядить конденсатор.
Процесс
зарядки конденсатора можно представить
как последовательный перенос достаточно
малых порций заряда Δq > 0
с одной обкладки на другую (рис. 1.7.1).
При этом одна обкладка постепенно
заряжается положительным зарядом, а
другая – отрицательным. Поскольку
каждая порция переносится в условиях,
когда на обкладках уже имеется некоторый
заряд q,
а между ними существует некоторая
разность потенциалов ![]() при
переносе каждой порции Δq внешние
силы должны совершить работу
при
переносе каждой порции Δq внешние
силы должны совершить работу 
Энергия Wе конденсатора емкости C, заряженного зарядом Q, может быть найдена путем интегрирования этого выражения в пределах от 0 до Q:
|
|
Рисунок 1.7.1. Процесс зарядки конденсатора |
Формулу, выражающую энергию заряженного конденсатора, можно переписать в другой эквивалентной форме, если воспользоваться соотношением Q = CU.
|
Электрическую энергию Wе следует рассматривать как потенциальную энергию, запасенную в заряженном конденсаторе. Формулы для Wе аналогичны формулам для потенциальной энергии Eрдеформированной пружины (см. ч. I, § 2.4)
|
где k – жесткость пружины, x – деформация, F = kx – внешняя сила.
По современным представлениям, электрическая энергия конденсатора локализована в пространстве между обкладками конденсатора, то есть в электрическом поле. Поэтому ее называют энергией электрического поля. Это легко проиллюстрировать на примере заряженного плоского конденсатора.
Напряженность однородного
поля в плоском конденсаторе равна E = U/d,
а его емкость  Поэтому
Поэтому
|
где V = Sd – объем пространства между обкладками, занятый электрическим полем. Из этого соотношения следует, что физическая величина
|
является электрической (потенциальной) энергией единицы объема пространства, в котором создано электрическое поле. Ее называют объемной плотностью электрической энергии.
Энергия поля, созданного любым распределением электрических зарядов в пространстве, может быть найдена путем интегрирования объемной плотности wе по всему объему, в котором создано электрическое поле.
17) Электрический ток.
Электри́ческий ток — направленное (упорядоченное) движение заряженных частиц[1][2][3].
Такими частицами могут являться: в металлах — электроны, в электролитах — ионы (катионы и анионы), в газах — ионы и электроны, в вакууме при определенных условиях — электроны, в полупроводниках — электроны и дырки (электронно-дырочная проводимость). Иногда электрическим током называют также ток смещения, возникающий в результате изменения во времени электрического поля[4].
Электрический ток имеет следующие проявления:
нагревание проводников (в сверхпроводниках не происходит выделения теплоты);
изменение химического состава проводников (наблюдается преимущественно в электролитах);
создание магнитного поля (проявляется у всех без исключения проводников)[3].
18) Закон Ома в обыкновенной и дифференциальной формах
Закон Ома в интегральной форме для однородного участка цепи (не содержащего ЭДС)
|
|
(7.6.1) |
|
Для однородного линейного проводника выразим R через ρ:
|
|
(7.6.2) |
|
ρ – удельное объемное сопротивление; [ρ] = [Ом·м].
Найдем
связь между ![]() и
и ![]() в
бесконечно малом объеме проводника
– закон
Ома в дифференциальной форме.
в
бесконечно малом объеме проводника
– закон
Ома в дифференциальной форме.
В изотропном проводнике (в данном случае с постоянным сопротивлением) носители зарядов движутся в направлении действия силы, т.е. вектор плотности тока и вектор напряженности поля коллинеарны (рис. 7.6).

Рис. 7.6
Исходя из закона Ома (7.6.1), имеем:

А
мы знаем, что ![]() или
или ![]() .
Отсюда можно записать
.
Отсюда можно записать
|
|
(7.6.3) |
|
это запись закона Ома в дифференциальной форме.
Здесь ![]() – удельная
электропроводность.
– удельная
электропроводность.
Размерность
σ – [![]() ].
].
Плотность
тока можно выразить через заряд
электрона е,
количество зарядов n и
дрейфовую скорость ![]() :
:
![]() .
.
Обозначим ![]() ,
тогда
,
тогда ![]() ;
;
|
|
(7.6.4) |
|
Теперь,
если удельную электропроводность σ
выразить через е, n и b: ![]() то
вновь получим выражение закона
Ома в дифференциальной форме:
то
вновь получим выражение закона
Ома в дифференциальной форме:
.
19) Параллельное и последовательное соединение проводников
Последовательное и параллельное соединения в электротехнике — два основных способа соединения элементов электрической цепи. При последовательном соединении все элементы связаны друг с другом так, что включающий их участок цепи не имеет ни одного узла. При параллельном соединении все входящие в цепь элементы объединены двумя узлами и не имеют связей с другими узлами, если это не противоречит условию.
При последовательном соединении проводников сила тока во всех проводниках одинакова.
При параллельном соединении падение напряжения между двумя узлами, объединяющими элементы цепи, одинаково для всех элементов. При этом величина, обратная общему сопротивлению цепи, равна сумме величин, обратных сопротивлениям параллельно включенных проводников.
При
последовательном соединении проводников
сила тока в любых частях цепи одна и та
же: ![]()
Полное
напряжение в цепи при последовательном
соединении, или напряжение на полюсах
источника тока, равно сумме напряжений
на отдельных участках цепи: ![]() 3
om + 5 om = 8 om
3
om + 5 om = 8 om
Резисторы[править | править вики-текст]

![]()
Катушка индуктивности[править | править вики-текст]

![]()
Электрический конденсатор[править | править вики-текст]

![]() .
.
Сила
тока в неразветвленной части цепи равна
сумме сил токов в отдельных параллельно
соединённых проводниках: ![]()
Напряжение
на участках цепи АВ и на концах всех
параллельно соединённых проводников
одно и то же: ![]()
Резисторы[править | править вики-текст]
При
параллельном соединении резисторов
складываются величины, обратно
пропорциональные сопротивлению (то
есть общая проводимость ![]() складывается
из проводимостей каждого резистора
складывается
из проводимостей каждого резистора ![]() )
)

![]()
Если цепь можно разбить на вложенные подблоки, последовательно или параллельно включённые между собой, то сначала считают сопротивление каждого подблока, потом заменяют каждый подблок его эквивалентным сопротивлением, таким образом находится общее (искомое) сопротивление.
20) Закон Джоуля-Ленца в обыкновенной и дифференциальной формах
Если
в проводнике течет постоянный ток и
проводник остается неподвижным, то
работа сторонних сил расходуется на
его нагревание. Опыт показывает, что в
любом проводнике происходит выделение
теплоты, равное работе, совершаемой
электрическими силами по переносу
заряда вдоль проводника. Если на концах
участка проводника имеется разность
потенциалов ![]() ,
тогда работу по переносу заряда q на
этом участке равна
,
тогда работу по переносу заряда q на
этом участке равна ![]()
По
определению I= q/t. откуда q= I t. Следовательно ![]()
Так как работа идет па нагревание проводника, то выделяющаяся в проводнике теплота Q равна работе электростатических сил
|
(17.13) |
Соотношение
(17.13) выражает закон Джоуля-Ленца в
интегральной форме. Введем плотность
тепловой мощности ![]() ,
равную энергии выделенной за единицу
время прохождения тока в каждой единице
объема проводника
,
равную энергии выделенной за единицу
время прохождения тока в каждой единице
объема проводника
![]()
где
S - поперечное сечение проводника, ![]() -
его длина. Используя (1.13) и соотношение
-
его длина. Используя (1.13) и соотношение ![]() ,
получим
,
получим
![]() Но
Но ![]() -
плотность тока, а
-
плотность тока, а ![]() ,
тогда
,
тогда
![]()
с
учетом закона Ома в дифференциальной
форме ![]() ,
окончательно получаем
,
окончательно получаем
|
(17.14) |
Формула (17.14) выражает закон Джоуля-Ленца в дифференциальной форме: объемная плотность тепловой мощности тока в проводнике равна произведению его удельной электрической проводимости на квадрат напряженности электрического поля.
21) Электрический ток в цепи с источником.
Исто́чник то́ка (в теории электрических цепей) — двухполюсник, создающий в нагрузке электрический ток, причем сила тока не зависит от сопротивления нагрузки. Используются также термины генератор тока и идеальный источник тока. Источник тока — модель реального источника электроэнергии или часть такой модели.
В быту «источником тока» называют реальные устройства-источники электрической энергии, например, батарейку (гальванический элемент, аккумулятор), электрогенератор, вторичный источник электропитания, электросеть 220 В и даже настенную розетку такой электросети. Некорректность состоит в смешении понятий реального объекта (источника электроэнергии) и его модели. Кроме того, с точки зрения теории электрических цепей, по своим техническим характеристикам большинство бытовых «источников тока» гораздо ближе к другой, противоположной источнику тока модели — источнику ЭДС. К модели источника тока близки, например, зарядные устройства аккумуляторов, узлы питания (балласты) газоразрядных и светодиодных ламп.
Источник тока[править | править вики-текст]
Напряжение на
клеммах источника тока (не
путать с реальным источником!)
зависит только от сопротивления ![]() нагрузки:
нагрузки:
![]()
Мощность, отдаваемая источником тока в нагрузку,
![]()
Поскольку
для источника тока ![]() ,
то напряжение на его клеммах и мощность,
передаваемая им в нагрузку, с ростом
сопротивления нагрузки возрастают,
достигая в пределе бесконечных значений.
,
то напряжение на его клеммах и мощность,
передаваемая им в нагрузку, с ростом
сопротивления нагрузки возрастают,
достигая в пределе бесконечных значений.
Реальный источник[править | править вики-текст]
Любой реальный
источник тока (не
путать с описанным выше источником тока
— моделью!)
в линейном приближении может быть описан
при помощи внутреннего
сопротивления ![]() .
Реальный источник представляется как
идеальный источник тока, соединенный
параллельно со внутренним сопротивлением.
Можно показать, что реальный источник
тока с внутренним сопротивлением
эквивалентен
реальному источнику ЭДС, имеющему
внутреннее сопротивление
и
ЭДС
.
Реальный источник представляется как
идеальный источник тока, соединенный
параллельно со внутренним сопротивлением.
Можно показать, что реальный источник
тока с внутренним сопротивлением
эквивалентен
реальному источнику ЭДС, имеющему
внутреннее сопротивление
и
ЭДС ![]() .
.
Напряжение на клеммах реального источника тока равно
![]()
Сила тока в цепи равна
![]()
Мощность, отдаваемая реальным источником тока в сеть, равна
![]()
Реальные генераторы тока имеют различные ограничения (например, по напряжению на его выходе), а также нелинейные зависимости от внешних условий. В частности, реальные генераторы тока создают электрический ток только в некотором диапазоне напряжений, верхний порог которого зависит от напряжения питания источника. Таким образом, реальные источники тока имеют ограничения по нагрузке.
22) Теорема о циркуляции вектора Е вдоль электрической цепи.
23) Электромагнетизм. История терминов
24) Вектор магнитной индукции, сила Ампера
На проводник с током, находящийся в магнитном поле, действует сила, равная
F = I·L·B·sina
I - сила тока в проводнике; B - модуль вектора индукции магнитного поля; L - длина проводника, находящегося в магнитном поле; a - угол между вектором магнитного поля инаправлением тока в проводнике.
Силу, действующую на проводник с током в магнитном поле, называют силой Ампера.
Максимальная сила Ампера равна:
F = I·L·B
Ей соответствует a = 900.

Направление силы Ампера определяется по правилу левой руки: если левую руку расположить так, чтобы перпендикулярная составляющая вектора магнитной индукции В входила в ладонь, а четыре вытянутых пальца были направлены по направлению тока, то отогнутый на 90 градусов большой палец покажет направление силы, действующей на отрезок проводника с током, то есть силы Ампера.
25) Закон Био-Савара-Лапласа. Принцип суперпозиции. Пример
Опыт, как уже отмечалось, свидетельствует о том, что источником магнитного поля является электрический ток. Но каким образом можно вычислить вектор магнитной индукции поля, зная этот ток?
Для магнитного поля, также как и для электрического, справедлив принцип суперпозиции электрических полей. Справедливость этого принципа нельзя доказать теоретически. Он подтверждается только экспериментально.
Суть этого принципа состоит в следующих двух положениях.
1)
Если ток I1 создаёт
в некоторой точке пространства магнитное
поле ![]() ,
то этот вектор магнитной индукции не
изменится при появлении других
токов: I2, I3,
…, In.
Это означает, что появление новых токов
и новых полей не искажает индукции
магнитного
поля исходного тока I1.
,
то этот вектор магнитной индукции не
изменится при появлении других
токов: I2, I3,
…, In.
Это означает, что появление новых токов
и новых полей не искажает индукции
магнитного
поля исходного тока I1.
2) Если магнитное поле создаётся несколькими токами, то индукция такого поля равна векторной сумме магнитных индукций складываемых полей:
![]() (8.4)
(8.4)
Эти положения многократно подтверждены экспериментально.
Теперь применим принцип суперпозиции для расчёта магнитного поля электрического тока: вектор магнитной индукции поля, созданного электрическим током, равен векторной сумме магнитных индукций от отдельных элементов этого тока:
![]() .
.
Для
окончательного решения этой задачи
нужно только знать, какое поле ![]() создаёт
элемент тока
создаёт
элемент тока ![]() .
.
В решении этой проблемы добились успеха французские учёные: физики экспериментаторы Био и Савар и математик Лаплас. Они установили, что вектор магнитной индукции поля, созданного элементом тока , равен:
![]() (закон
Био-Савара-Лапласа, 1820 г.), (8.5)
(закон
Био-Савара-Лапласа, 1820 г.), (8.5)
здесь: — элемент тока;
![]() —
радиус-вектор,
проведённый от элемента тока в точку,
где вычисляется магнитное поле (рис.
8.5.)
—
радиус-вектор,
проведённый от элемента тока в точку,
где вычисляется магнитное поле (рис.
8.5.)

Рис. 8.5.
Таким образом, был найден «элементарный кирпичик» магнитного поля. Зная поле элемента тока (8.5), можно теперь, опираясь на принцип суперпозиции магнитных полей, рассчитать поле любого тока.
Прежде, чем перейти к примерам расчёта магнитных полей, напомним, что точно тот же самый метод мы использовали и при рассмотрении электростатических полей. Что являлось «элементарным кирпичиком» электростатического поля? Поле точечного заряда. А далее, используя принцип суперпозиции электрических полей, мы получали возможность рассчитать поле любого заряда, разделяя его на составляющие точечные заряды.




 ,
,





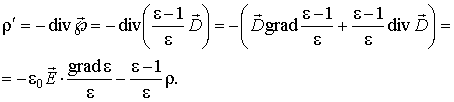


 (сферический конденсатор),
(сферический конденсатор),
 (цилиндрический конденсатор).
(цилиндрический конденсатор).