
- •Плоские электромагнитные волны в поглощающей среде. Скорость волны. Глубина проникновения. Поверхностный импеданс металлов. Скин-слой. Поток мощности.
- •Дисперсия волн. Волновой пакет. Фазовая и групповая скорости. Нормальная и аномальная дисперсии. Дисперсионное уравнение.
- •4. Прохождение плоской волны через границу раздела двух сред. Коэффициенты Френеля. Явление полного внутреннего отражения. Угол Брюстера. Приближенные граничные условия Леонтовича.
- •Волны в анизотропных средах
- •Продольное распространение плоской волны в намагниченной плазме
- •Поперечное распространение в намагниченной плазме
- •Электромагнитные волны в направляющих системах. Те, тм и тем волны. Критическая частота. Длина волны в направляющей системе. Волновое сопротивление линии передачи.
- •Уравнения геометрической оптики для электромагнитных волн
- •Условия применимости геометрической оптики
ФИЗИКА ВОЛНОВЫХ ПРОЦЕССОВ
Волновое уравнение. Гармонические волны. Уравнение Гельмгольца. Фазовый фронт, фазовая скорость, длина волны. Стоячие волны. Неоднородные плоские волны. Цилиндрические и сферические волны.
Плоские электромагнитные волны в поглощающей среде. Глубина проникновения. Поток мощности. Скорость волны. Поверхностный импеданс металлов. Скин-слой.
Дисперсия волн. Волновой пакет. Фазовая и групповая скорости. Нормальная и аномальная дисперсии. Дисперсионное уравнение.
Прохождение плоской волны через границу раздела двух сред. Коэффициенты Френеля. Явление полного внутреннего отражения. Угол Брюстера. Приближенные граничные условия Леонтовича.
Плоские электромагнитные волны в анизотропных средах. Продольное и поперечное распространение в намагниченной плазме. Обыкновенная и необыкновенная волны. Эффекты Фарадея и Коттона-Мутона.
Излучение волн. Ближняя и дальняя зоны. Диаграмма направленности линейного излучателя. Понятие области мнимых углов. Излучение волн плоским раскрывом.
Электромагнитные волны в направляющих системах. ТЕ, ТМ и ТЕМ волны. Критическая частота. Длина волны в направляющей системе. Волновое сопротивление линии передачи.
Приближение геометрической оптики. Уравнение эйконала. Световые лучи. Область применимости лучевого приближения. Принцип Ферма. Рефракция.
Волновое уравнение. Гармонические волны. Уравнение Гельмгольца. Фазовый фронт, фазовая скорость, длина волны. Стоячие волны. Неоднородные плоские волны. Цилиндрические и сферические волны.
Зададим некоторое возмущение, распространяющееся в пространстве, в виде U=U(at–bs), где t – текущее время; s – пространственная координата, вдоль которой распространяется возмущение, и продифференцируем 2 раза по t и 2 раза по s:
![]()
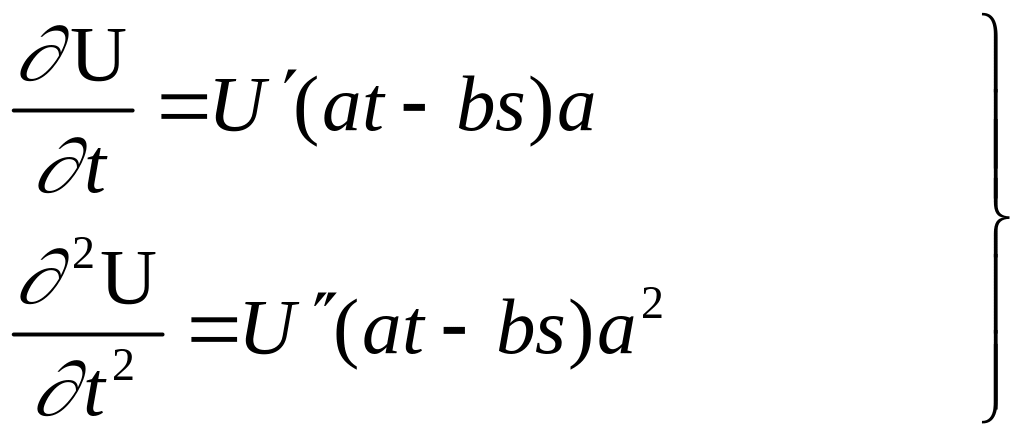 (1)
(1)
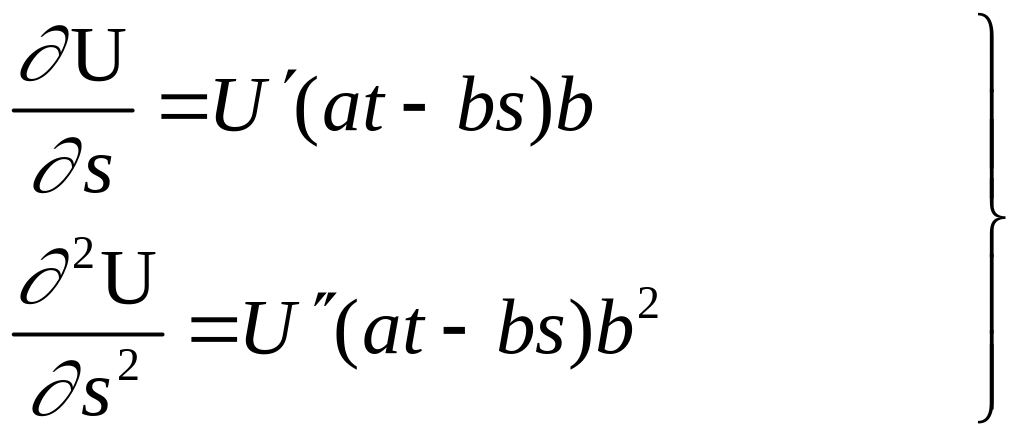 (2)
(2)
сравнивая
(1) и (2) и учитывая, что
![]() ,
где v
– скорость распространения возмущения,
убеждаемся, что U(s,t)
удовлетворяет однородному дифференциальному
уравнению в частных производных второго
порядка гиперболического типа (уравнению
Даламбера),
которое принято называть волновым
уравнением:
,
где v
– скорость распространения возмущения,
убеждаемся, что U(s,t)
удовлетворяет однородному дифференциальному
уравнению в частных производных второго
порядка гиперболического типа (уравнению
Даламбера),
которое принято называть волновым
уравнением:
![]() (1-я
каноническая
форма).
(1-я
каноническая
форма).
Перейдя
к характеристическим переменным
![]() ,
можем записать уравнение в виде
,
можем записать уравнение в виде
![]() (2-я каноническая
форма). Эти
уравнения описывают распространение
возмущения в пространстве в виде
свободных
волн. Интегрируя
последнее уравнение, находим решение
в виде суперпозиции двух волн:
(2-я каноническая
форма). Эти
уравнения описывают распространение
возмущения в пространстве в виде
свободных
волн. Интегрируя
последнее уравнение, находим решение
в виде суперпозиции двух волн:
![]() ,
первая из которых является уходящей,
а вторая – приходящей.
Волны, соответствующие решению
однородного волнового уравнения,
называются свободными
волнами.
,
первая из которых является уходящей,
а вторая – приходящей.
Волны, соответствующие решению
однородного волнового уравнения,
называются свободными
волнами.
Здесь
предполагается, что U изменяется только
в одном направлении s,
задаваемом единичным вектором m,
тогда s
= (mr)
(r
– радиус-вектор
точки наблюдения). В некоторый момент
времени t=to
U(t)
= const, если s
= const. Т.к. (mr)
= const – уравнение плоскости, то
![]() представляет собой плоскую
волну,
бегущую в направлении m.
Аргумент t
определяет фазу
волны. Плоскость,
на которой фаза постоянна (фазовый
фронт, поверхность равных фаз)
перемещается в пространстве со скоростью
v
(фазовая
скорость).
представляет собой плоскую
волну,
бегущую в направлении m.
Аргумент t
определяет фазу
волны. Плоскость,
на которой фаза постоянна (фазовый
фронт, поверхность равных фаз)
перемещается в пространстве со скоростью
v
(фазовая
скорость).
Если
![]() ,
то функция U может быть представлена в
виде интеграла Фурье
,
то функция U может быть представлена в
виде интеграла Фурье
![]() (образ). Подставив U(s,t)
в волновое уравнение, видим что она
будет решением, если ее образ F(s,w)
удовлетворяет уравнению
(образ). Подставив U(s,t)
в волновое уравнение, видим что она
будет решением, если ее образ F(s,w)
удовлетворяет уравнению
![]()
(приведенное
волновое уравнение
или уравнение Гельмгольца).
Это уравнение описывает распространение
гармонических
свободных волн. Величина
![]() определяет пространственную периодичность
функции F
и называется волновым
числом.
Решение уравнения Гельмгольца
определяет пространственную периодичность
функции F
и называется волновым
числом.
Решение уравнения Гельмгольца
![]() представляет суперпозицию двух
гармонических
волн c
амплитудами
A1,
A2
и фазами
(t+–ks),
(t++ks),
бегущих
навстречу друг другу. Расстояние, которое
гармоническая волна пробегает за период
колебаний Т, или расстояние между точками
с одинаковой фазой колебаний называется
длина волны
.
Тогда k=
представляет суперпозицию двух
гармонических
волн c
амплитудами
A1,
A2
и фазами
(t+–ks),
(t++ks),
бегущих
навстречу друг другу. Расстояние, которое
гармоническая волна пробегает за период
колебаний Т, или расстояние между точками
с одинаковой фазой колебаний называется
длина волны
.
Тогда k=![]() .
Пусть начальные фазы
и
равны нулю. При А2=
0 имеем уходящую
бегущую гармоническую
волну
.
Пусть начальные фазы
и
равны нулю. При А2=
0 имеем уходящую
бегущую гармоническую
волну
![]() ,
а при А1=0
– приходящую
бегущую гармоническую
волну
,
а при А1=0
– приходящую
бегущую гармоническую
волну
![]() .
Если А1=А2=А,
то
.
Если А1=А2=А,
то
![]() ,
т.е. решение представляет собой синфазное
гармоническое колебание, амплитуда
которого имеет периодическую
пространственную зависимость с
периодичностью /2.
Такую ситуацию называют стоячая
волна. Точки,
в которых F(s)
имеет максимум или минимум называют,
соответственно, пучностями
и узлами
стоячей волны.
Расстояние между соседними узлами (или
пучностями) называется длиной
стоячей волны
ст
= /2.
,
т.е. решение представляет собой синфазное
гармоническое колебание, амплитуда
которого имеет периодическую
пространственную зависимость с
периодичностью /2.
Такую ситуацию называют стоячая
волна. Точки,
в которых F(s)
имеет максимум или минимум называют,
соответственно, пучностями
и узлами
стоячей волны.
Расстояние между соседними узлами (или
пучностями) называется длиной
стоячей волны
ст
= /2.
Если волна распространяется в направлении единичного вектора m, можем ввести вектор k = km (волновой вектор), тогда ks = (kr), и поверхность равных фаз ks = const определяется уравнением плоскости (kr) = const, нормальной к направлению распространения волны. Если k – вещественный вектор, то А=const всюду. Такая волна называется однородной плоской волной.
Функция F удовлетворяет однородному уравнению Гельмгольца и в том случае, если
k=k¢+ik²
но при условии,
что |k|2
= k2
– вещественно, т.е. (k¢k²)
= 0, а |k¢|2–|k²|2
= k2.
В этом случае решение
![]() описывает неоднородную
плоскую гармоническую волну,
у которой поверхность
равных фаз и
поверхность
равных амплитуд
– плоскости, ортогональные
друг другу, а скорость меньше, чем у
однородной волны с той же частотой и в
той же среде.
описывает неоднородную
плоскую гармоническую волну,
у которой поверхность
равных фаз и
поверхность
равных амплитуд
– плоскости, ортогональные
друг другу, а скорость меньше, чем у
однородной волны с той же частотой и в
той же среде.
Для
произвольной зависимости от координат
однородное волновое уравнение имеет
следующий вид
![]() .
Чтобы плоская волна распространялась
в направлении оси х
(в прямоугольной системе координат),
должно выполняться
.
Чтобы плоская волна распространялась
в направлении оси х
(в прямоугольной системе координат),
должно выполняться
![]() ,
т.е. источником плоской волны является
бесконечная плоскость y0z.
,
т.е. источником плоской волны является
бесконечная плоскость y0z.
В
цилиндрических координатах
![]() .
Если возмущение исходит от бесконечного
цилиндра, то
.
Если возмущение исходит от бесконечного
цилиндра, то
![]() ,
и волновое уравнение имеет вид
,
и волновое уравнение имеет вид
![]() .
После несложных преобразований его
можно привести к виду:
.
После несложных преобразований его
можно привести к виду:
![]() .
При больших значениях r
имеем
.
При больших значениях r
имеем
![]() .
Решением этого уравнения является
.
Решением этого уравнения является
![]() откуда следует, что поверхность равных
фаз – цилиндр, а амплитуда волны убывает
пропорционально
откуда следует, что поверхность равных
фаз – цилиндр, а амплитуда волны убывает
пропорционально
![]() .
Такая волна называется цилиндрической.
.
Такая волна называется цилиндрической.
В
сферических координатах
![]() . При точечном источнике
. При точечном источнике
![]() волновое уравнение можно представить
в виде:
волновое уравнение можно представить
в виде:
![]() .
Его решение –
.
Его решение –
![]() .
В этом случае поверхность равных фаз –
сфера, и амплитуда уходящей волны убывает
как
.
В этом случае поверхность равных фаз –
сфера, и амплитуда уходящей волны убывает
как
![]() .
Такая волна называется сферической.
.
Такая волна называется сферической.
Литература:
1. Виноградова М. Б., Руденко О. В., Сухоруков А. П. Теория волн. - М.: Наука, 1979.
2. Вайнштейн Л. А. Электромагнитные волны. - М.: Радио и связь, 1988.
Плоские электромагнитные волны в поглощающей среде. Скорость волны. Глубина проникновения. Поверхностный импеданс металлов. Скин-слой. Поток мощности.
В средах с потерями
(
0) имеем: [H]
= iE+E
= i (
- i /)E
= i![]() E,
где
=
E,
где
=![]() -
-![]() =
-
i
/
= =
(1-itg), tg
=
/
- тангенс угла электрических потерь.
= 0отн,;
=0отн
;. (отн=10-9/36
[Ф/м],
=
-
i
/
= =
(1-itg), tg
=
/
- тангенс угла электрических потерь.
= 0отн,;
=0отн
;. (отн=10-9/36
[Ф/м],
отн=
410-7[Гн/м]
). Пусть в такой
среде вдоль оси z
распространяется плоская гармоническая
волна, удовлетворяющая уравнениям:
![]() ,
где волновое число
,
где волновое число
![]() =
=
![]() оказывается
комплексной величиной:
=
оказывается
комплексной величиной:
=![]() =
- i..
Из соотношения
2
(1–itg)
= (
– i)2,
находим:
=
- i..
Из соотношения
2
(1–itg)
= (
– i)2,
находим:
![]() ,
,
![]() .
Решение для
уходящей волны: Ex=E0
e–
ze–i
z,
Hy=
.
Решение для
уходящей волны: Ex=E0
e–
ze–i
z,
Hy=![]() e–ze–i
z
e–ze–i
z
Здесь:
– коэффициент
затухания,
– коэффициент
фазы, Zo –
волновое сопротивление среды![]() ,
,
![]() ,
( 0/2</4),
vф=(
/)=1/
,
( 0/2</4),
vф=(
/)=1/![]() cos
(/2)
cos
(/2)
Таким образом, в поглощающей среде амплитуда уходящей волны убывает по экспоненциальному закону,
уменьшаясь в
e раз на расстоянии
d=1/,
которое называется глубина
проникновения
(скин-слой),
длина
волны =2/
и
фазовая
скорость
vф=
/
уменьшаются
по сравнению
с непоглощающей средой,
в среде с электрическими потерями Ну
отстает по фазе
от Еx
на величину
/2 (в среде с
магнитными потерями, когда комплексной
величиной
является
, Ну
опережает
Еx),
поверхность
равных фаз совпадает с поверхностью
равных амплитуд.
Для
сред с tg
>>1 (металлы)
![]() ,
/2,
v =
,
/2,
v =![]() ,
,![]() ,
ZS=
,
ZS=![]() – поверхностный
импеданс металла.
На границе с хорошо проводящей средой
используются приближенные граничные
условия: [En]
= ZS[n[nH]]
- граничные
условия Леонтовича.
– поверхностный
импеданс металла.
На границе с хорошо проводящей средой
используются приближенные граничные
условия: [En]
= ZS[n[nH]]
- граничные
условия Леонтовича.
В среде с потерями поток мощности через единицу поверхности П=[EH] становится комплексным.
Мгновенное значение Пz равно
Пz=![]() cos(
t-
z)cos(
t-
z
-/2)
=
[cos2(t-z)cos(/2)
+ 0.5sin2(
t-
z)sin(/2)].
Первое слагаемое
определяет пульсирующий поток, т.е.
мощность, переносимую волной, второе –
колеблющийся с удвоенной частотой поток
мощности, среднее за период значение
которого равно нулю (часть периода поток
мощности направлен в обратную сторону).
Скорость переноса энергии определяется
отношением среднего за период потока
мощности к средней плотности энергии
vэ = Пср/Wср.
В плоской
свободной волне запас электрической
энергии равен запасу магнитной энергии
Wэ
= Wм,
следовательно Wср=
0,5 Re(Wэ+
Wм)
= Re(|
cos(
t-
z)cos(
t-
z
-/2)
=
[cos2(t-z)cos(/2)
+ 0.5sin2(
t-
z)sin(/2)].
Первое слагаемое
определяет пульсирующий поток, т.е.
мощность, переносимую волной, второе –
колеблющийся с удвоенной частотой поток
мощности, среднее за период значение
которого равно нулю (часть периода поток
мощности направлен в обратную сторону).
Скорость переноса энергии определяется
отношением среднего за период потока
мощности к средней плотности энергии
vэ = Пср/Wср.
В плоской
свободной волне запас электрической
энергии равен запасу магнитной энергии
Wэ
= Wм,
следовательно Wср=
0,5 Re(Wэ+
Wм)
= Re(|![]() |
|![]() e-i
+
e-i
+![]()
![]() )
= |
|
(cos
+1)=|
|
)
= |
|
(cos
+1)=|
|![]() cos2
(/2).
Пср=0.5Re(
e-i/2)=
=
cos2
(/2).
Пср=0.5Re(
e-i/2)=
=![]() cos
/2
. Таким образом, vэ
= 1/
cos
(/2),
т.е. при наличии
потерь скорость переноса энергии
становится меньше.
cos
/2
. Таким образом, vэ
= 1/
cos
(/2),
т.е. при наличии
потерь скорость переноса энергии
становится меньше.
На рисунке показана
временная зависимость вещественной
(сплошная линия) и мнимой (пунктирная
линия) частей вектора Пойнтинга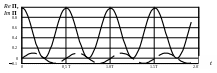
.
Литература:
1. Виноградова М. Б., Руденко О. В., Сухоруков А. П. Теория волн. - М.: Наука, 1979.
2. Вайнштейн Л. А. Электромагнитные волны. - М.: Радио и связь, 1988
3. Матвеев А. Н. Оптика.- М.: Высш. школа, 1985.
Дисперсия волн. Волновой пакет. Фазовая и групповая скорости. Нормальная и аномальная дисперсии. Дисперсионное уравнение.
Плоская гармоническая
волна, распространяющаяся вдоль z,
имеет вид: E
= Eoe–
ze–
i
(z
– t),
где в общем случае
,
.
Для плоской волны должно быть: dt
–dz
= 0, откуда
![]() –
фазовая
скорость (скорость
перемещения фазового фронта). Если ,
то vф,
причем может быть vф
> c.
Означает ли это, что можно передать
информацию со скоростью, превышающей
скорость света с
?
–
фазовая
скорость (скорость
перемещения фазового фронта). Если ,
то vф,
причем может быть vф
> c.
Означает ли это, что можно передать
информацию со скоростью, превышающей
скорость света с
?
Рассмотрим
распространение колебания более сложной
формы (сигнал). Пусть в точке z
= 0 имеется
сигнал f(t)
с амплитудным спектром
![]() .
Каждой составляющей спектра соответствует
плоская гармоническая волна, следовательно
в точке z
> 0 имеем:
.
Каждой составляющей спектра соответствует
плоская гармоническая волна, следовательно
в точке z
> 0 имеем:
![]() .
Если ,
можем перейти к пространственному
спектру, т.е. dd,
тогда
.
Если ,
можем перейти к пространственному
спектру, т.е. dd,
тогда
![]() .
Выделим вблизи максимума огибающей
спектра с частотой о
участок спектра 2
1
2.
Пусть
<<0
, тогда
.
Выделим вблизи максимума огибающей
спектра с частотой о
участок спектра 2
1
2.
Пусть
<<0
, тогда
![]() ,
где 0
= 0
/v0.
Этот участок спектра можно рассматривать
как группу
волн или
волновой
пакет.
Полагая в первом приближении
,
где 0
= 0
/v0.
Этот участок спектра можно рассматривать
как группу
волн или
волновой
пакет.
Полагая в первом приближении
![]() и используя замену переменной
0
, получаем:
и используя замену переменной
0
, получаем:
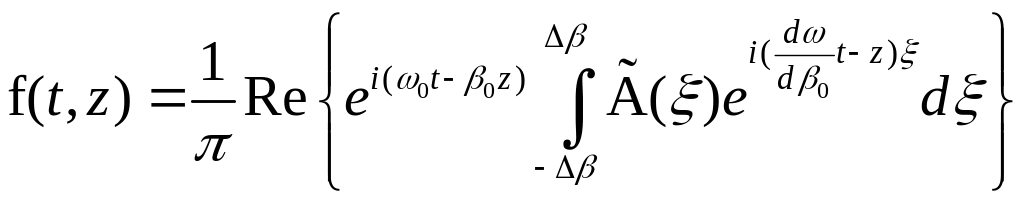 .
Если
.
Если
![]() =
const,
этот интеграл
легко вычисляется, и в результате имеем:
=
const,
этот интеграл
легко вычисляется, и в результате имеем:
 ,
где множитель в фигурных скобках
представляет собой огибающую спектра
сигнала (амплитуда волны) F(t,z).
Максимум огибающей, соответствующий
условию
,
где множитель в фигурных скобках
представляет собой огибающую спектра
сигнала (амплитуда волны) F(t,z).
Максимум огибающей, соответствующий
условию
![]() =
0, и прилегающая к нему группа
волн
перемещается в пространстве со скоростью
=
0, и прилегающая к нему группа
волн
перемещается в пространстве со скоростью
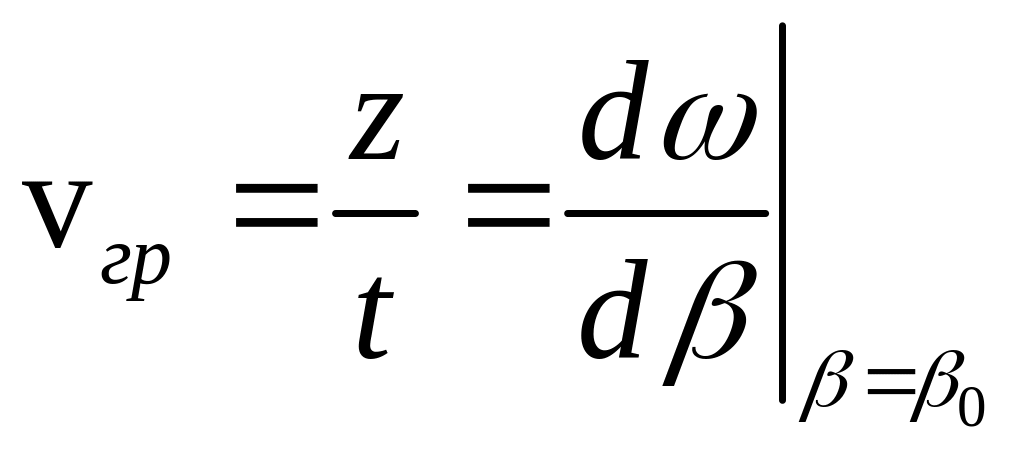 ,
которая называется групповой
скоростью.
,
которая называется групповой
скоростью.
Связь между
фазовой
скоростью
vф
и групповой
скоростью
vгр:
![]() . т.к.
. т.к.
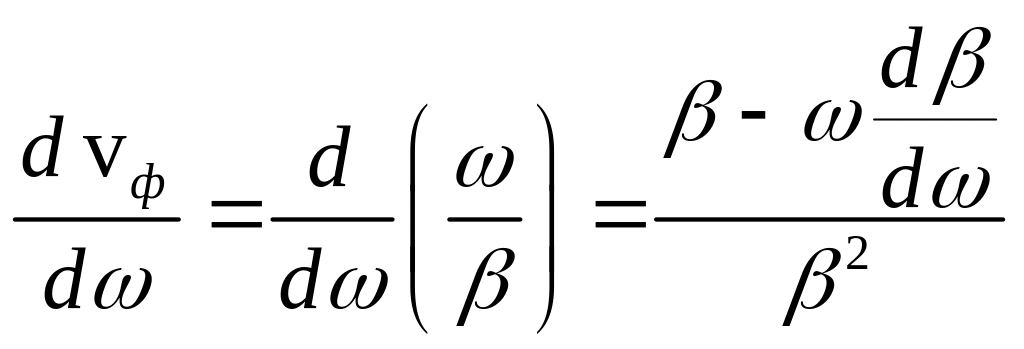 ,
имеем:
,
имеем:
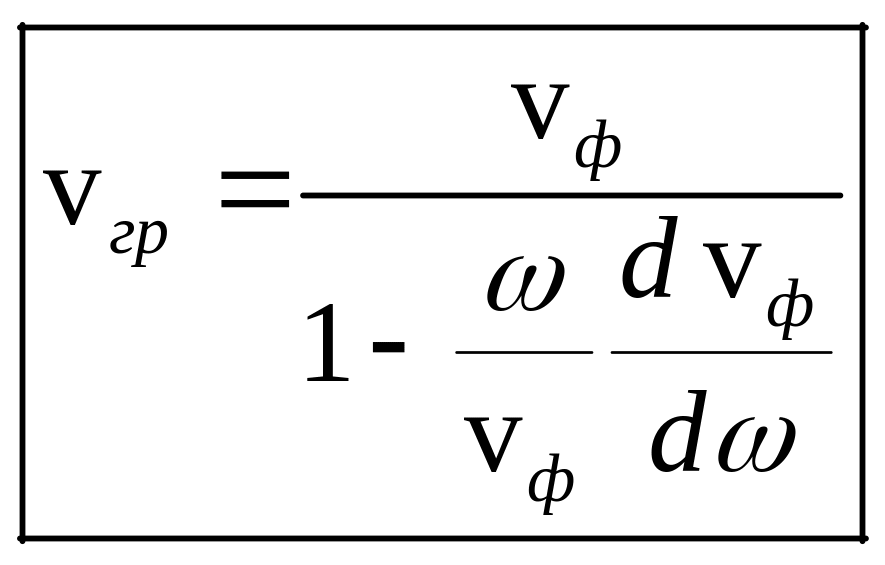 . Если
. Если
![]() ,
то vгр≠vф
и существует дисперсия
– зависимость vф
от частоты. Если
,
то vгр≠vф
и существует дисперсия
– зависимость vф
от частоты. Если
![]() ,
дисперсии нет и vгр=
vф.
,
дисперсии нет и vгр=
vф.
Виды дисперсии:
vгр<vф
(vф
~1/ω) – нормальная;
vгр>vф
(vф
~ ω) – аномальная.
Если
![]() совпадают
по направлению – дисперсия положительная,
Если
имеют
противоположные направления – дисперсия
отрицательная.
Отрицательной аномальной дисперсии
быть не может. Если vгр
имеет физический смысл, то это скорость
переноса энергии.
совпадают
по направлению – дисперсия положительная,
Если
имеют
противоположные направления – дисперсия
отрицательная.
Отрицательной аномальной дисперсии
быть не может. Если vгр
имеет физический смысл, то это скорость
переноса энергии.
Дисперсионное
уравнение. В
произвольных линейных средах без
искажений может распространяться только
плоские гармонические волны, удовлетворяющие
уравнению (p)
= 0, где
– линейный
однородный оператор (для сред, подчиняющихся
волновому уравнению
=![]() ).
Чтобы гармоническая волна сохраняла
форму при любой частоте, необходимо,
чтобы в числе решений было решение вида:
p
= ei
t
i (kr).
Пусть
переводит р
в некоторую
функцию q:
(
p)
= q.
Если q0,
то p
– свободная волна в данной среде.
Продифференцируем по t,
учитывая линейность и однородность :
).
Чтобы гармоническая волна сохраняла
форму при любой частоте, необходимо,
чтобы в числе решений было решение вида:
p
= ei
t
i (kr).
Пусть
переводит р
в некоторую
функцию q:
(
p)
= q.
Если q0,
то p
– свободная волна в данной среде.
Продифференцируем по t,
учитывая линейность и однородность :
![]() ,
т.е.
,
т.е.
![]() ,
где комплексная амплитуда
,
где комплексная амплитуда
![]() не зависит от t,
но может зависеть от .
Подставив p
и q
в уравнение (
p)
= q,
получим уравнение, не зависящее от t,
и содержащее
как параметр. Если продифференцировать
по координатам, получим: q=(p)=(ikp)=
ik(p)=
ikq,
т.е. q=ikq,
следовательно, можно представить q
в виде: q=f(,k)ei
t
i(kr),
где f(,k)
кроме
и k
может зависеть
только от коэффициентов оператора. При
произвольных
и k
p
= ei
t
i (kr)
не свободная волна,
т.к. не является решением уравнения
(
p)
= 0. Чтобы определить, какие свободные
волны могут распространяться (имеют
право на существование) в данной среде,
необходимо выбрать такие
и k,
чтобы
не зависит от t,
но может зависеть от .
Подставив p
и q
в уравнение (
p)
= q,
получим уравнение, не зависящее от t,
и содержащее
как параметр. Если продифференцировать
по координатам, получим: q=(p)=(ikp)=
ik(p)=
ikq,
т.е. q=ikq,
следовательно, можно представить q
в виде: q=f(,k)ei
t
i(kr),
где f(,k)
кроме
и k
может зависеть
только от коэффициентов оператора. При
произвольных
и k
p
= ei
t
i (kr)
не свободная волна,
т.к. не является решением уравнения
(
p)
= 0. Чтобы определить, какие свободные
волны могут распространяться (имеют
право на существование) в данной среде,
необходимо выбрать такие
и k,
чтобы
![]() .
Это уравнение
называют дисперсионным
уравнением.
Каждому
значению
соответствует решение этого уравнения
относительно
k,
и каждому k
– относительно .
Для изотропной среды это уравнение
содержит только |k|
и его можно привести к виду
.
Это уравнение
называют дисперсионным
уравнением.
Каждому
значению
соответствует решение этого уравнения
относительно
k,
и каждому k
– относительно .
Для изотропной среды это уравнение
содержит только |k|
и его можно привести к виду
![]() – дисперсионное
уравнение для данной среды.
– дисперсионное
уравнение для данной среды.
Примеры:
а) Дисперсионное уравнение, соответствующее волновому уравнению, есть k2 – 2 c2, где с – const. В этом случае vф = с, дисперсии нет.
б) Для волн на
поверхности воды потенциал скорости
удовлетворяет уравнениям 2
= 0,
![]() .
Ищем волну в виде:
еi
t
– i
k
x
– k
z.
Получаем
дисперсионное уравнение:
.
Ищем волну в виде:
еi
t
– i
k
x
– k
z.
Получаем
дисперсионное уравнение:
![]() .
Отсюда vф=
g
/,
т.е. vф
зависит от ,
следовательно, существует нормальная
дисперсия
(vф1/).
.
Отсюда vф=
g
/,
т.е. vф
зависит от ,
следовательно, существует нормальная
дисперсия
(vф1/).
в) Уравнение
поперечного смещения стержня при малых
колебаниях имеет вид:
![]() ,
где G
– коэффициент изгибной жесткости. Ищем
решение в виде: еi
t
– i
k
x,
получаем
дисперсионное уравнение
,
где G
– коэффициент изгибной жесткости. Ищем
решение в виде: еi
t
– i
k
x,
получаем
дисперсионное уравнение
![]() ,
откуда
,
откуда
![]() ,
т.е. имеется аномальная
дисперсия
(vф).
,
т.е. имеется аномальная
дисперсия
(vф).
Литература.
Виноградова М. Б., Руденко О. В., Сухоруков А. П. Теория волн. - М.: Наука, 1979.
Исакович М. А. Общая акустика. - М.: Наука, 1978.
