Розподіл Больцмана у загальному вигляді

Розподіл Больцмана можна представити й у більш загальному вигляді. Дійсно, число молекул dN, що знаходяться в елементарному об’ємі dV=dxdydz біля точки (x,y,z) і мають , можна записати як:

Отже,

(10)

Поділимо формулу (10) на N і позначимо , тоді:

(11)

або

(12)

Формули (11) і (12) виражають закон Больцмана у загальному вигляді. Стала Больцмана В – для кожного потенціального поля має свої значення. Стала В знаходиться з умови нормування функції розподілу Больцмана. Ймовірність виявлення молекули у всьому об’ємі:



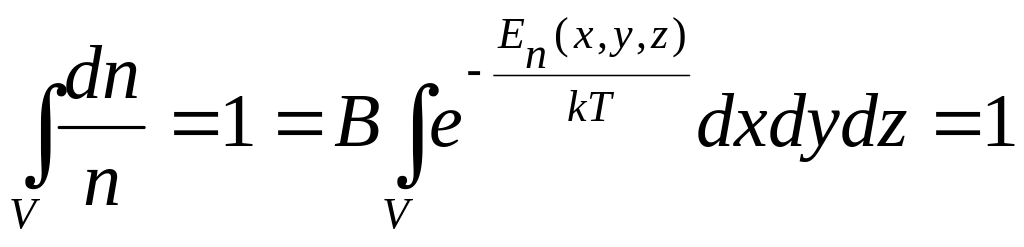
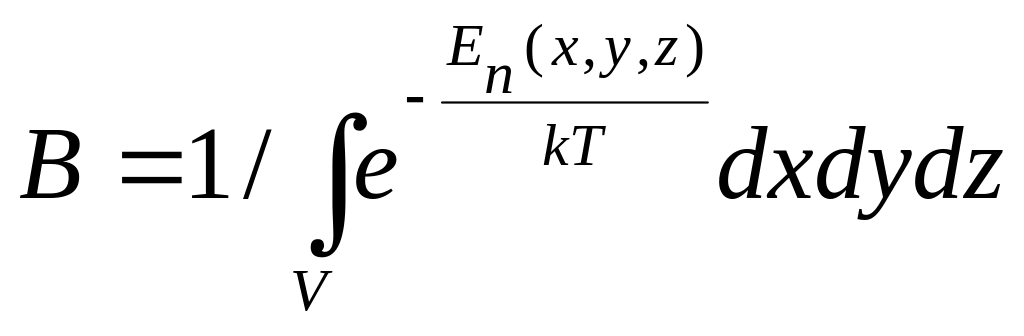
У випадку, коли розглядається рух молекул у полі тяжіння Землі:

Повернемось до формул (11) і (12). Вони дають нам ймовірність виявлення будь-якої з молекул з потенціальною енергією в околі точки простору з координатами . З цих формул також можна отримати і часткові випадки. Наприклад, для системи молекул, що рухаються в полі сили тяжіння Землі, , тобто отримаємо формулу (13).

Тоді



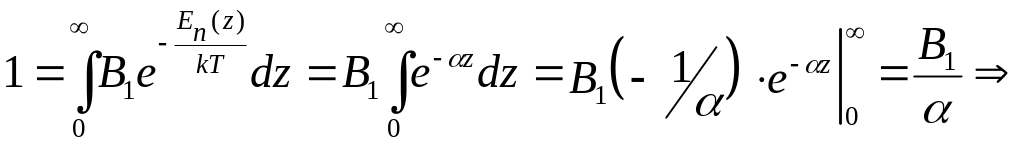
Таким чином:

;

Розподіл Максвела-Больцмана

Розподіл Максвела (за швидкостями) і розподіл Больцмана (за потенціальними енергіями) можна об’єднати в єдиний закон розподілу молекул Максвела-Больцмана. При цьому розподіл Больцмана описується в просторі координат x, y, z, а розподіл Максвела в просторі швидкостей x, y, z.

     Якщо ввести 6-мірний простір, координатами молекули в якому є величини x, y, z, x, y, z, то функція розподілу в такому просторі буде залежати від цих шістьох змінних: n(x, y, z, x, y, z). Вважаючи просторові змінні x, y, z і компоненти швидкості x, y, z статистично незалежними друг від друга, то можна перемножити розподіл Максвела і розподіл Больцмана, тоді отримаємо

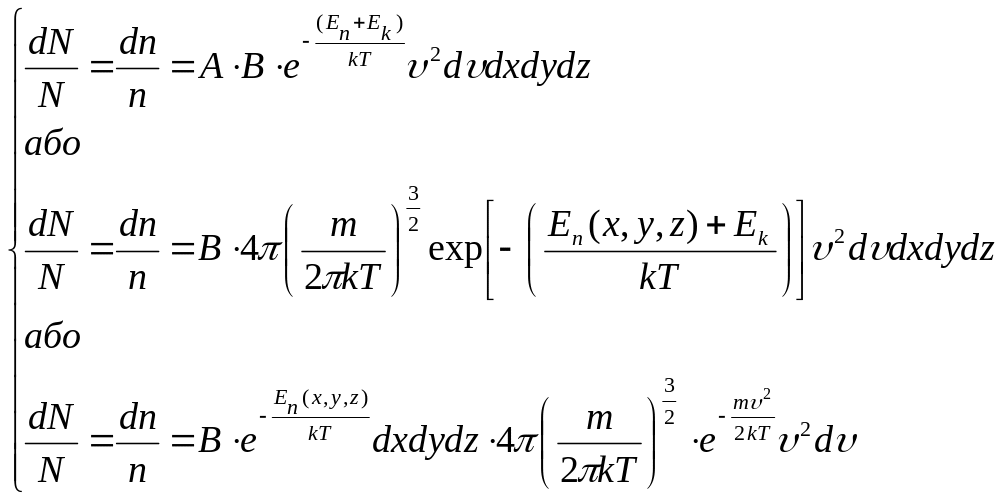
(13)

Будь-яке рівняння (13) дає нам відносну кількість частинок, які, маючи потенціальну енергію , знаходяться в околі точки і одночасно мають швидкості (модулі швидкостей) в межах від  до  + d поблизу швидкості .

Можна казати інакше:

– це ймовірність виявлення частинки з потенціальною енергією в околі точки , яка має одночасно швидкість в інтервалі від  до  + d поблизу швидкості .

Розподіл Максвела-Больцмана використовують у випадку, коли повна енергія молекули Е дорівнює сумі її потенціальної енергії Е_п у зовнішньому силовому полі і кінетичної енергії Е_к її поступального руху: Е= Е_п+ Е_к.

Броунівський рух (розрахунок зміщення броунівської частинки). Досліди перрена по визначенню числа авогадро Суть броунівського руху

Англійський ботанік Броун у 1827 році виявив, що дрібні частинки , наприклад, спори папороті, які зважені у воді, здійснюють неперервні хаотичні рухи. Такий хаотичний рух дрібних частинок, що зважені у рідині або газі, отримав назву броунівського.

Швидкість руху броунівських частинок збільшується зі зростанням температури та зі зменшенням розмірів частинок ( ). Характер броунівського руху не залежить від властивостей речовини частинок, а залежить лише від властивостей рідини чи газу, в яких ці частинки зважені.

Вказані закономірності можна пояснити, якщо припустити, що броунівський рух виникає внаслідок ударів з боку молекул рідини або газу, в яких зважені рухомі частинки.

Оскільки рух молекул хаотичний, ми могли б очікувати на те, що число ударів з боку молекул о частинку в будь-якому напрямку дорівнюватиме числу ударів у протилежному напрямку. В результаті ж усі поштовхи повинні компенсувати один одного, і частинка залишиться нерухомою. Але це твердження буде справедливе лише для великих проміжків часу, і тільки в середньому число ударів у різних напрямках буде однаковим. Якщо ж мова йде про малі проміжки часу і малі об’єми рідини чи газу, а також випадки, коли число ударів N – невелике, то можливі відхилення від середніх значень.

Такі відхилення від середнього значення будь якої величини, які виникають в малому об’ємі але за мали проміжки часу називаються флуктуаціями. І оскільки ми розглядаємо малі частинки, то для них переважання ударів з якого-небудь боку буде помітним, отже і флуктуації значні, що призведе до броунівського руху.

Таким чином, броунівський рух пояснюється тим, що, завдяки флуктуації числа ударів молекул о частинку, виникає деяка результуюча сила певного напрямку. Оскільки флуктуація звичайно є недовгочасною, то через деякий проміжок часу напрямок результуючої сили змінюється, а разом з ним змінюється і напрям переміщення частинки.

В результаті мають місце хаотичні (“судорожні”) рухи частинок, що зважені у рідині або газі, які відображають хаотичність молекулярного руху.

Іншими словами, броунівський рух – це результат переважання числа ударів одного напрямку над числом ударів протилежного напрямку (за малий проміжок часу), а не результат удару однієї молекули.

Виведення рівняння Ейнштейна-Смолуховського для броунівського руху

Як ми з’ясували раніше, внаслідок неповної компенсації ударів молекул з протилежних боків, на броунівську частинку діє на протязі короткого часу деяка сила F. Окрім неї, на частинку, яка рухається за рахунок сили F, діє ще сила тертя , що напрямлена супроти F.

Пам’ятаємо, що сила тертя (сила Стокса):

 = (1)

де а– радіус частинки, – швидкість її руху, – коефіцієнт внутрішнього тертя (в’язкості).

Тоді рівняння руху частинки (для випадку одномірного руху) буде мати вигляд:



(2)

Ми записали це рівняння в проекціях на вісь x. Тепер наша задача полягає в тому, щоб знайти середнє значення зміщення x частинки, яке відбувається за час t внаслідок ударів молекул. Точніше, потрібно знайти середнє значення багатьох послідовних переміщень  ,  ,...,  , які відбулися за рівні проміжки часу  =  = ... =  . Оскільки окремі переміщення  відрізняються як за величиною, так і за напрямком, то їх сума, а отже і , можуть виявитися рівними нулю. У зв’язку з цим задача зводиться до знаходження середнього значення квадрату зміщення, тобто величини .

Тому перетворимо (2) таким чином, щоб ця формула включала в себе . Помножимо обидві частини рівняння на x:

(3)

При цьому:

Підставимо отримані рівності у (3):

(4)

Оскільки ця рівність справедлива для довільного зміщення , то вона буде виконуватися і для середніх значень величин, які входять до неї, , якщо зміщень було досить багато:

(5),

де – середнє значення квадрату зміщення частинки, – середнє значення квадрату її швидкості, , оскільки x і можуть однаково часто приймати додатні і від’ємні значення.

Таким чином, рівняння (5) приймає вигляд:

(6)

Зауважимо, що – середнє значення проекцій швидкості на вісь x. В силу хаотичності руху частинки:

= =

Вочевидь також:

= = =

Отже:

=

Тому

= = = =

де = = – середня кінетична енергія броунівського руху частинок.

Зіштовхуючись з молекулами, броунівська частинка обмінюється з ними енергією і знаходиться у стані теплової рівноваги з середовищем (рідиною), у якому рухається. Тому броунівської частинки повинна дорівнювати молекул рідини або газу, остання ж дорівнює .

Закон рівномірного розподілу кінетичної енергії за ступенями вільності читається так:

Якщо термодинамічна система знаходиться в стані теплової рівноваги при температурі T, то середня кінетична енергія рівномірно розподілена за всіма ступенями вільності і для кожної з них дорівнює .

Таким чином, якщо число ступенів вільності для молекули дорівнює і, то середня енергія молекули:

Ось чому:

= (7)

Рівняння (6) з урахуванням (7) перепишеться у вигляді:

(8)

Позначимо =

Одержимо новий вираз:

(9)

Розділимо у цьому рівнянні змінні:

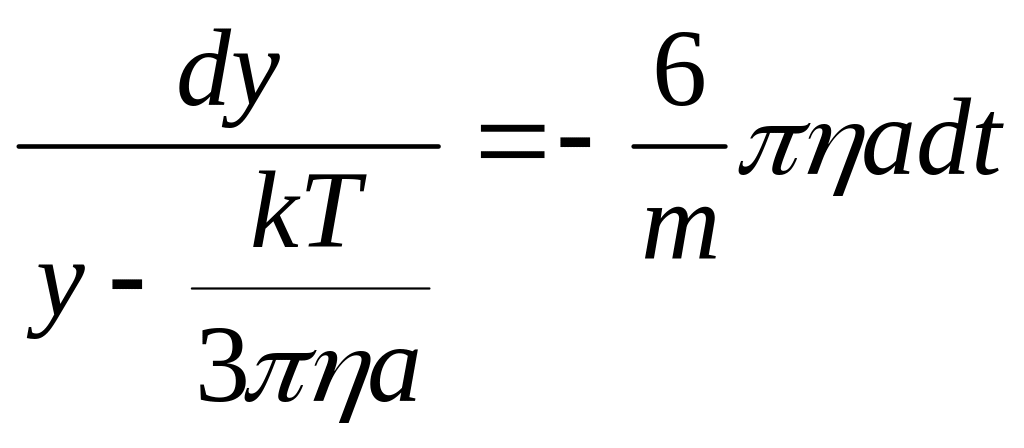
Отриманий вираз проінтегруємо: ліву частину – у межах від 0 до y, а праву – від 0 до t. В результаті:

=

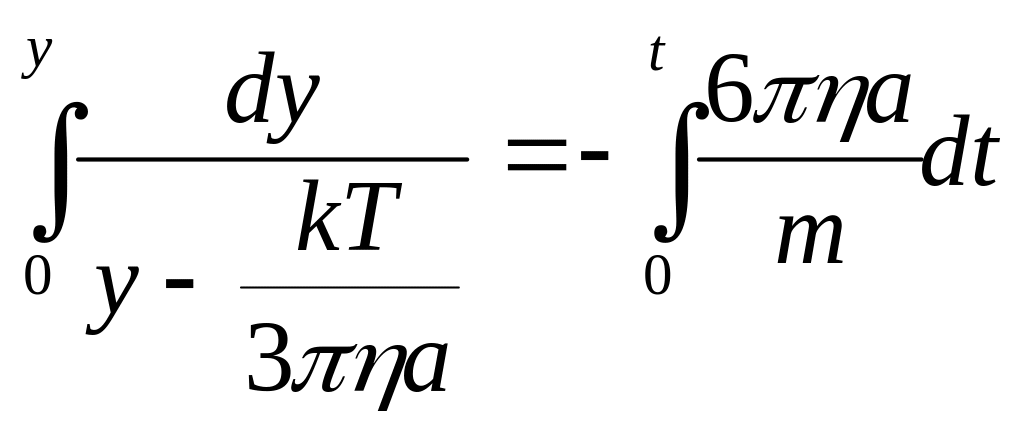
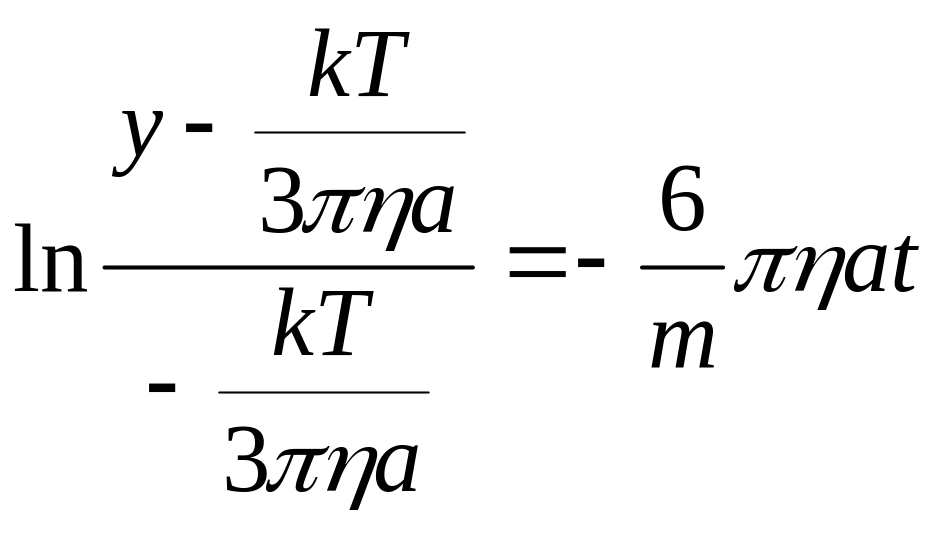
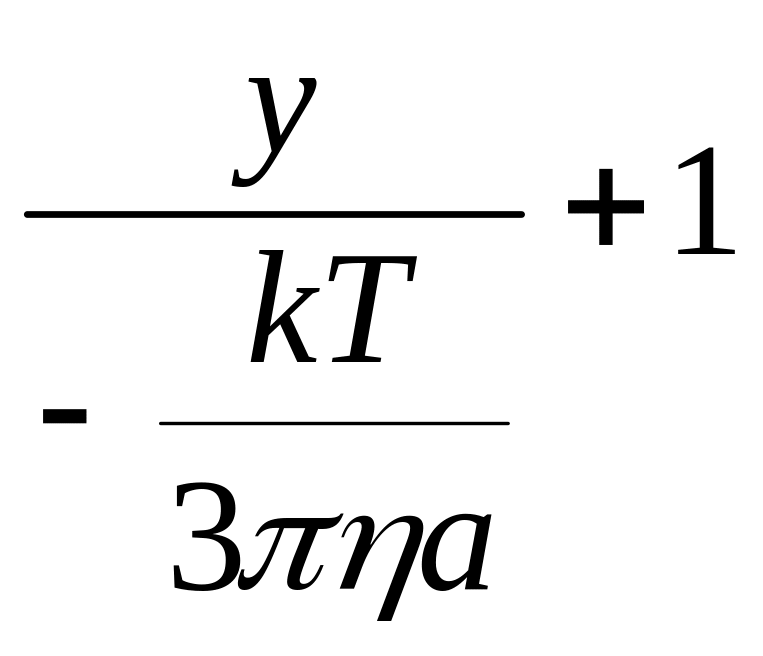(10)

Проаналізуємо отриману рівність. У звичайних умовах а см,   , таким чином дріб приймає досить великі значення при с. А це означає, що величиною можна знехтувати. В результаті:

(11)

Для кінцевих проміжків часу t і відповідних переміщень рівняння Ейнштейна-Смолуховського можна записати у вигляді:

t (12)

Середнє значення квадратів багатьох переміщень броунівської частинки за проміжок часу t вздовж вісі x (або будь-якої іншої) пропорційне цьому проміжку часу.

Підтвердження броунівського руху дослідами Перрена та визначення числа Авогадро

Перреном у 1909 році був проведений дослід, у якому спостерігалися і фіксувалися послідовні переміщення частинки. Для цього об’єктив його мікроскопу був поділений сіткою ліній, що дозволяло визначати положення однієї броунівської частинки через рівні проміжки часу (30 с). Поєднавши потім точки, які визначали положення частинки, він отримав картину відрізків – ламану лінію. Обчисливши середнє значення квадратів цих послідовних переміщень:

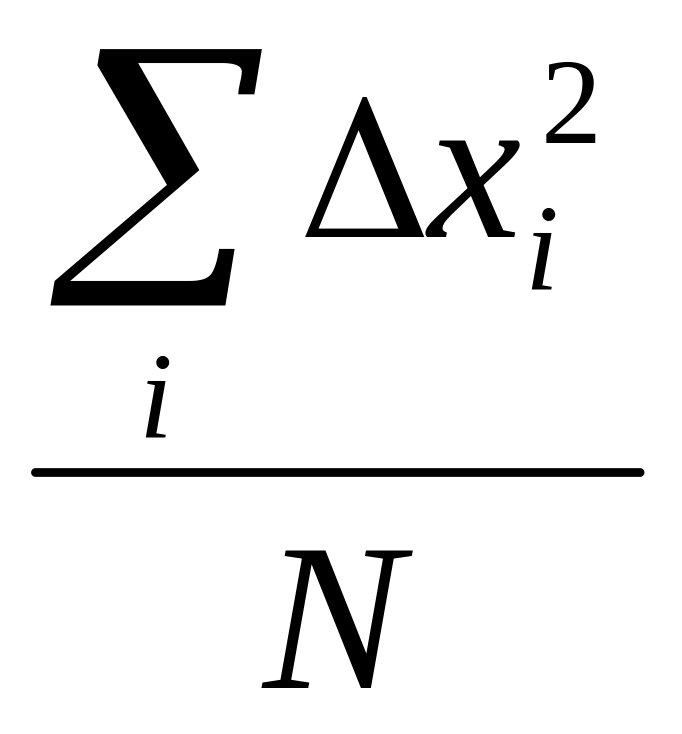= (N – число зміщень),

Перрен з’ясував, що добре узгоджується з формулою (12). Тим самим була підтверджена правильність пояснення явища броунівського руху в рамках молекулярно-кінетичної теорії і, вочевидь, самої цієї теорії.

Перрен використав отримані їм дані для визначення числа Авогадро за формулою:

при чому k визначав за даними експерименту, а R було взято як відому величину.

Таким чином, досліди Перрена мали велике значення для остаточного підтвердження молекулярно-кінетичної теорії.

КІНЕМАТИЧНІ ХАРАКТЕРИСТИКИ МОЛЕКУЛЯРНОГО РУХУ. (ПОПЕРЕЧНИЙ ПЕРЕРІЗ, СЕРЕДНЯ ДОВЖИНА ВІЛЬНОГО ПРОБІГУ)

При встановленні стану термодинамічної рівноваги в системі з молекул газу важливу роль відіграють зіткнення між молекулами. Власне кажучи, зіткнення молекул є результатом їхньої взаємодії.

Внаслідок зіткнення, молекули можуть відхилятися від свого прямолінійного шляху (розсіюватися), можуть ділитися на більш прості частинки (дисоціювати), наприклад, на атоми, тощо. Зазначимо, що зміна напрямку руху молекул в результаті зіткнення називається розсіюванням.

Зміна напрямку руху молекул викликана силами їх взаємодії, які помітні лише на малих відстанях між молекулами. Тоді відхилення молекул від початкового напрямку трапляється тільки за умови їх достатнього зближення. Зміна напрямку руху молекули на помітний кут під дією іншої молекули назвемо зіткненням молекул.

Розглядаючи зіткнення між молекулами ми будемо їх уявляти твердими пружними кулями. Таке припущення виправдовується тим, що інколи молекули дійсно поводяться наче тверді пружні кулі. Але між молекулами діють сили притягання і відштовхування, які залежать від відстані між молекулами -“кулями”. Незважаючи на те, що в цьому випадку можна казати про зіткнення “поверхонь” молекул, їх розміри можна визначити як відстань між їхніми центрами при зіткненні.