Рівняння стану ідеального газу

Величини, що визначають стан газу - тиск р, температуру Т і об'єм V, який займає визначена маса газу - називаються параметрами стану. Параметри не є незалежними, кожен з них є функцією двох інших.

Рівняння, що зв'язує тиск р, температуру Т і об'єм V для даної маси газу називається рівнянням стану, і може бути записане у загальному вигляді:

F (p,V,T)=0.

Тобто, стан газу визначається двома будь-якими параметрами, третій параметр однозначно визначається двома іншими.

Співвідношення

p = nkT, (10)

що поєднує тиск газу з його температурою і концентрацією молекул, отримано для моделі ідеального газу, молекули якого взаємодіють між собою і зі стінками посудини тільки під час пружних зіткнень. Це співвідношення може бути записане в іншій формі, що встановлює зв'язок між макроскопічними параметрами газу – об'ємом V, тиском p, температурою T і кількістю речовини ν.

Якщо в об'ємі V міститься N часток, то і маємо

(11)

В це рівняння входять усі три параметри стану, тому воно є рівнянням стану ідеального газу.

Але число N неможливо виміряти безпосередньо, тож його треба замінити на масу газу М, яку досить легко виміряти. Для цього перетворення скористуємось поняттям про моль. Як відомо, моль будь-якої речовини містить одну й ту ж саму кількість молекул (по визначенню), яка дорівнює числу Авогадро N_A = 6,0210²³. Число молів речовини в даній масі дорівнює: , звідси число молекул у даній масі газу .

У підсумку одержимо:

(12)

Добуток числа Авогадро N_A на сталу Больцмана  k називається універсальною газовою сталою і позначається буквою R. Її чисельне значення в СІ є:

R = 8,31 Дж/моль·К.

Співвідношення

(13)

називається рівнянням стану ідеального газу і вперше було записане Д. І. Менделєєвим.

Для одного моля будь-якого газу це співвідношення приймає вид:

pV=RT (14)

Це рівняння, що встановлює зв'язок між тиском, об'ємом і температурою 1 молю газу було отримано в середині XIX століття французьким фізиком Б. Клапейроном. Тому рівняння стану газу називається рівнянням Клапейрона–Менделєєва.

Закони ідеального газу

Зміна стану газу, що супроводжується зміною всіх або декількох параметрів, називають газовим процесом. Якщо процес протікає досить повільно, то в будь-який момент система близька до свого рівноважного стану. Такі процеси називаються квазістатичними. Інтерес представляють процеси, у яких один з параметрів (p, V або T) залишається незмінним. Такі процеси називаються ізопроцесами.

Ізотермічний процес (T = const)

Ізотермічним процесом називають квазістатичний процес, що протікає при постійній температурі T. pV = const Цю формулу називають рівнянням ізотерми або законом Бойля-Маріотта. Його фізичний зміст: зміна об’єму газу супроводжується такою зміною тиску, що добуток тиску на об’єм залишається величиною постійною при незмінній масі.

Рисунок 3 - Сімейство ізотерм на площині (p, V). T3 > T2 > T1

Ізохорний процес (V = const)

Ізохорний процес – це процес квазістатичного нагрівання або охолодження газу при постійному об'ємі V і за умови, що кількість речовини ν у посудині залишається незмінною: . рівняння ізохорного процесу називається законом Шарля. На площині (p, T) ізохорні процеси для заданої кількості речовини ν при різних значеннях об'єму V зображуються сімейством прямих ліній, що називаються ізохорами.

Рисунок 4 - Сімейство ізохор на площині (p, T). V3 > V2 > V1

Ізобарний процес (p = const)

Ізобарним процесом називають квазістатичний процес, що протікає при незмінному тиску p. Рівняння ізобарного процесу для деякої незмінної кількості речовини ν має вигляд: На площині (V, T) ізобарні процеси при різних значеннях тиску p зображуються сімейством прямих ліній (рис.  6), що називаються ізобарами. рівняння ізобарного процесу називають законом Гей-Люссака.

Рисунок 6 - Сімейство ізобар на площині (V, T). p3 > p2 > p1

Закон Авогадро (1811 р.)

При однакових тисках і температурах у рівних об'ємах будь-якого газу міститься однакове число молекул.

Для двох різних газів однакового об'єму при однакових тисках і температурах рівняння стану має вигляд:

pV = N₁kТ , pV = N₂kТ, отже N₁ = N₂ (24)

де N₁, N₂ – число молекул у кожному з об'ємів.

З закону випливає, що моль будь-якого газу при даних тиску і температурі займає однаковий об'єм. Зокрема, при нормальних умовах t° = 0°С (273,15 К) і p₀ = 1атм (1,0110⁵ [н⁄м²] = [Па])

м³⁄моль = 22,4 м³⁄кмоль = 22,4 л ⁄ моль

а число молекул, що міститься при нормальних умовах у 1 м³ газу дорівнює:

м^-3 - число Лошмідта.

Закон Дальтона (1801 р.)

Тиск газової суміші дорівнює сумі парціальних тисків її компонентів:

p = p₁ + p₂ + … (25)

Нехай в посудині об’ємом V у стані теплової рівноваги знаходиться суміш різних газів, які хімічно не реагують один з одним. Для такої суміші рівняння стану має вигляд:

pV = (N₁ + N₂ + ...+N_i+…)kT,

де N_i- число молекул i-го компонента суміші.

Тиск суміші дорівнює

, (26)

Цей вираз показує, що кожна група молекул чинить тиск, незалежний від того, який тиск чинять інші молекули. Це зумовлено тим, що в ідеальному газі між молекулами відсутня взаємодія.

Тиск являє собою тиск кожного з компонентів суміші, що займає об’єм , тобто парціальний тиск. Парціальний тиск - тиск, який би чинив газ, якби він один займав увесь об’єм, що займає суміш.

Дослід показує, що при достатньо високих тисках, коли гази вже не можна вважати ідеальними, спостерігаються відхилення (в той чи інший бік) від закону Дальтона.

Загальна назва приладу, з допомогою якого визначають температуру, - термометр. Якщо привести термометр у тепловий контакт із тілом, температуру якого необхідно виміряти, то через деякий час встановиться термодинамічна рівновага між термометром та тілом. Це дозволяє приписати тілу значення температури, що показує термометр. Виходячи з такого принципу вимірювань, одразу випливають вимоги до термометрів – вони не повинні змінювати стан тіла, температура якого вимірюється. Цього можна досягти зменшенням розмірів термометрів. (Пригадайте розміри відомих вам термометрів.)

Щоб визначити температуру кількісно, вводять температурну шкалу – систему правил, з допомогою якої кожна температура може бути охарактеризована певним числом. Проградуйований за даним правилом прилад, називається термометром. Основний елемент термометра – термометричне тіло – тіло, яке приводять у контакт із об’єктом, температуру якого необхідно визначити. Фізична величина, яка виступає в якості індикатора температури називається термометричною величиною. Приклади:

Рідинні термометри: т.т. – рідина, т.в. – її об’єм.

Термометри опору: т.т. – металевий дріт або напівпровідник, т.в. – електроопір.

Термопарні термометри: т.т. – термопара, т.в. – е.р.с.

Процедура введення температурної шкали наступна. Обирають термометричну величину – позначимо її буквою а. При нагріванні вона повинна змінюватись монотонно. Інакше не буде однозначного зв’язку між а та Т. З цього випливає, що об’єм води, наприклад, не підходить в якості термометричної величини, оскільки при 4^оС він має мінімальне значення. Далі, між а і Т обирають характер зв’язку:

Т = f(а).

Зв’язок може бути довільним, і отже з допомогою одного і того ж термометра можна побудувати нескінченну кількість температурних шкал. Найпростіший випадок – лінійна однорідна функція

Т = Аа.

Вибір константи дасть одиницю температури – градус. На практиці роблять навпаки. Величину А знаходять, призначаючи певній точці певне значення температури або двом точкам – різницю температур. Такі точки називають реперними.

Приклад. До 1954 р. температурна шкала будувалась по двом реперним точкам – нормальній точці кипіння води Т_к та нормальній точці плавлення льоду Т_пл. За означенням, приймалось, що різниця температур цих точок рівна 100^о. Для А маємо

,

де а_к та а_пл – значення термометричної величини у відповідних точках. Між тим краще відтворюється потрійна точка води, в якій у тепловій рівновазі знаходяться всі три фази – лід, вода і пара. В абсолютній термодинамічній шкалі температур або шкалі Кельвіна приймається, що температура цієї точки рівна 273.16 градусів точно. В цьому випадку для А маємо

.

Такий вибір дозволяє зберегти зв’язок із шкалою, в якій використовувались дві реперні точки, тобто різниця Т_к - Т_пл = 100 град, якщо в якості термометричного тіла використовується ідеальний газ.

Виходячи з вищесказаного, можна дати наступне означення:

емпіричною температурою називають визначену з досліду міру відхилення термодинамічного стану тіла від стану теплової рівноваги із льодом, який тане при нормальному тиску.

Існує безліч емпіричних температурних шкал, які відрізняються одна від одної термометричною величиною. Показники таких термометрів співпадають лише в реперних точках. Тобто ртутний, спиртовий, із мідного дроту термометри при визначенні температури одного і того ж тіла дадуть різні значення.

Але температура – об’єктивна міра інтенсивності теплового руху. З цієї точки зору перевагу надають якомусь одному типу термометрів і інші градуюють за основним.

Ідеально-газова шкала температур

Відомо, що ідеальні гази з досить великою точністю підкоряються закону Бойля-Маріотта: добуток об’єму даної маси газу на тиск цього газу залежить лише від температури. Цей добуток можна прийняти в якості термометричної величини, а сам газ - термометричним тілом. В цьому випадку (1) ми можемо записати

PV = CT

C – залежить від маси та і хімічної природи газу.

Досвід показує, що визначена температура з допомогою ідеально-газової шкали, дуже слабо залежить від хімічного складу. Температуру визначають за зміною об’єму при постійному тиску, чи за зміною тиску при постійному об’ємі. Останній спосіб легше реалізується.

При Т = 0, рівняння дає Р = 0. Кажуть, що це одна із найменших температур – абсолютний нуль. Але це твердження має екстраполяційний характер і не має доказів, оскільки при низьких температурах газ конденсується. Строго існування абсолютного нуля доводиться лише на основі другого начала термодинаміки. Шкала, в якій відлік температури ведеться від абсолютного нуля називається абсолютною шкалою.

З формули випливає, що нулем температури є температура, при якій середня кінетична енергія хаотичних рухів молекул дорівнює нулеві. Але тільки теплова енергія, оскільки уявлення про спокій частинок суперечить принципу невизначеності Гейзенберга.

Друге начало термодинаміки дозволяє строго визначити температурну шкалу, яка не залежить ані від речовини, ані від обраного параметру. Така шкала називається абсолютною термодинамічною шкалою.

На практиці використовується Міжнародна практична температурна шкала, яка максимально відтворює термодинамічну шкалу. В ній перераховуються 11 реперних точок, за якими градуюються стандартні термометри. Одиниці вимірювання – градус Цельсія або кельвін в залежності від початку відліку температури.

РОЗПОДІЛ МАКСВЕЛА (РОЗПОДІЛ МОЛЕКУЛ ЗА ШВИДКОСТЯМИ). АНАЛІЗ ЗАКОНУ МАКСВЕЛА. ХАРАКТЕРНІ ШВИДКОСТІ РОЗПОДІЛУ МАКСВЕЛА. ЕКСПЕРИМЕНТАЛЬНА ПЕРЕВІРКА ЗАКОНУ

Розподіл Максвела (розподіл молекул за швидкостями)

Раніше ми з’ясували, що в системі мікрочастинок з часом встановлюється термодинамічна рівновага. Це відбувається внаслідок зіткнень між молекулами, в результаті яких проекції швидкості молекул випадково змінюються на d_x, d_y і d_z , причому ці зміни не залежать друг від друга. Швидкості молекул розподіляються за певним законом. Цей закон виражається за допомогою так званої функції розподілу . Вигляд цієї функції і закон розподілу молекул за швидкостями, встановив у 1859 році англійський фізик Джеймс Кларк Максвел

 (1)

Таким чином можна сказати, що  – ймовірність виявлення у молекули будь-якого газу швидкості  в одиничному інтервалі d. Або, іншими словами,  дає нам відносне число молекул, швидкості яких лежать в одиничному інтервалі d поблизу швидкості .

Знайдемо аналітичний вигляд функції . Виразимо швидкість молекули в декартових координатах через її компоненти x, y, z (тобто через її проекції на вісі OX, OY, OZ):

(2)

Використовуючи (1) і (2), можемо записати:

(3)

Фізично ці вирази мають такий зміст: dnx – це частина молекул із загального їх числа n, які мають швидкості x, що напрямлені вздовж осі OX і лежать в інтервалі dx. Аналогічно визначається фізичний зміст dny , dnz .

Вирази (3) можна переписати дещо по-іншому:

(4)

В цьому випадку кажемо, що Wx – це ймовірність виявлення у молекули складової x вектора швидкості  в інтервалі dx . Так само визначаються Wy і Wz .

Припустимо, що імовірності знаходження значень проекцій швидкості молекули x, y і z у відповідних інтервалах dx, dy і dz не залежать друг від друга, тобто значення проекцій швидкості молекул на ортогональні осі вважаються статистично незалежними величинами. Тоді згідно теореми множення ймовірностей незалежних випадкових величин, маємо:

=xyz) dx dy dz (5)

де x,y,z) – функції розподілу значень відповідних проекцій швидкості x, y і z, причому вигляд цих функцій повинен бути однаковим, тому що всі вісі координат рівноправні.

Вираз (5) означає, що ймовірність W(x, y, z) виявити у молекули вектор швидкості  з компонентами x, y, z, які лежать відповідно в інтервалах dx, dy, dz, дорівнює добутку незалежних величин Wx Wy Wz.

Очевидно, що, внаслідок хаотичного руху молекул і стану термодинамічної рівноваги у газі, різні напрямки швидкостей молекул є рівноймовірними.

А тому вказана ймовірність W(x, y, z) не залежить від напрямку вектора швидкості (але залежить від  ). Тобто ймовірність W(x, y, z) не буде змінюватися зі зміною проекцій швидкості на вісі координат x, y, z. Але при цьому повинен залишатись сталим модуль швидкості  . При цих умовах:

x y z) = const (6)

Тоді

d x y z)  = 0 (7)

Розкриємо повний диференціал:

x y z)dx+x y z)dy+xy z)dz = 0 (8)

Розділимо (8) на вираз (6):

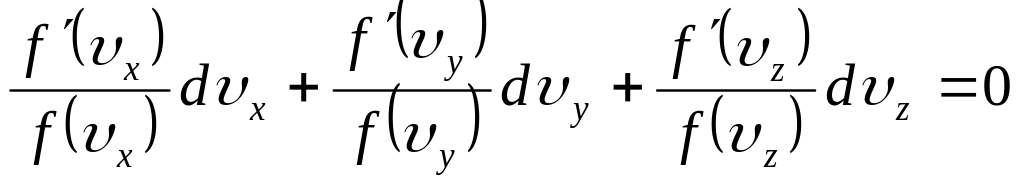(9)

Пригадаємо, що при зміні компонентів швидкості x, y, z модуль цієї швидкості залишиться сталим. Тобто:

(10)

Продиференцюємо останній вираз:

x dx + y dy + z dz = 0 (11)

Помножимо (11) на якийсь поки що невизначений множник  і результат складемо з виразом (9):

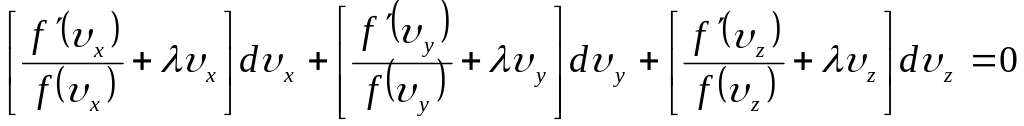(12)

Отримана рівність буде справедливою лише тоді, коли кожний вираз у квадратних дужках дорівнюватиме нулю:

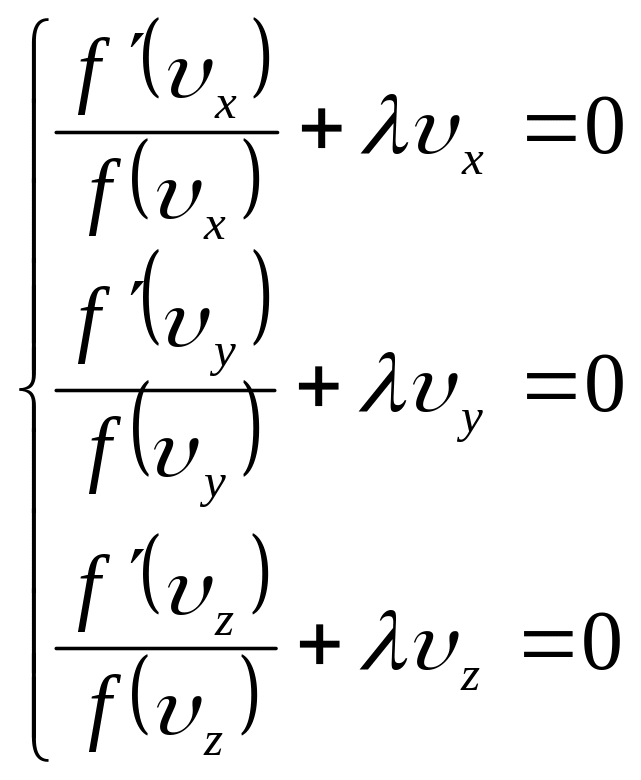(13)

Проінтегруємо вирази (13):

 (14)

Сталу інтегрування С знайдемо з умови нормування функції розподілу ймовірностей. Пригадаємо, що:

Підставимо в ці формули значення x, y, z) з (14) і проінтегруємо отримані вирази по всім можливим швидкостям від - до + . При цьому врахуємо, що, згідно умові нормування, Wx, Wy i Wz будуть дорівнювати 1. В результаті отримаємо:

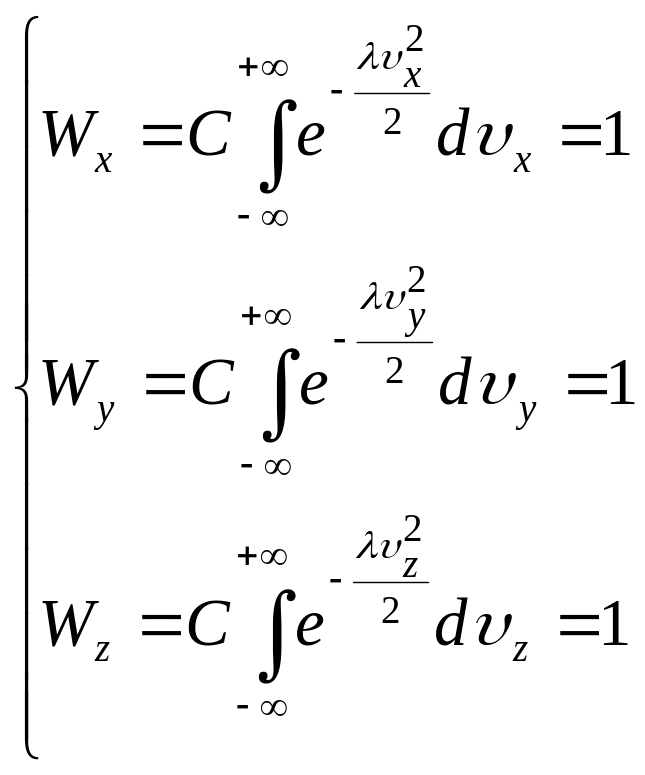(15)

Оскільки інтеграл Пуассона дорівнює то, зробивши відповідні перетворення у формулах (15), можемо знайти сталу С:

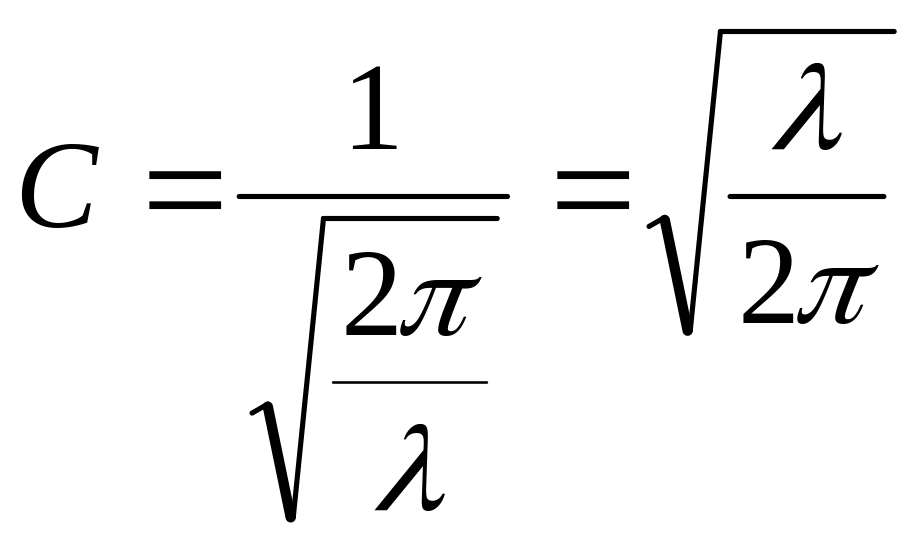(16)

Підставимо отримане значення С у формули (14):

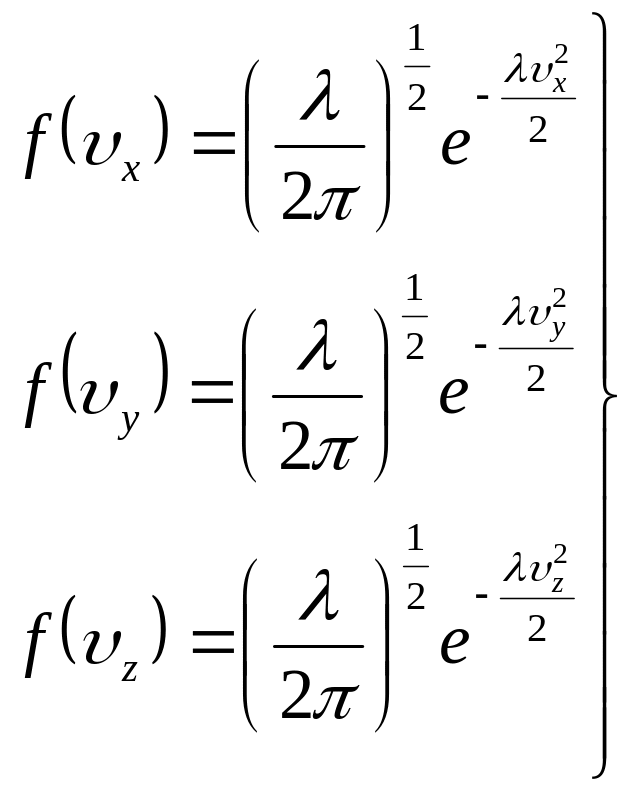(17)

Залишається визначити . Нам відомо, що середнє значення квадратів швидкостей молекул дорівнює:

(оскільки )

З іншого боку,

Тоді можемо стверджувати, що:

Оскільки напрямки швидкостей молекул є рівноймовірними, то

Або

(18)

З іншого боку , можна визначити як середнє значення випадкової величини за допомогою теорії ймовірностей:

Підставимо в дану формулу значення з рівняння (17):

На підставі наслідку інтегралу Пуассона , маємо що



 (19)

Прирівнюємо (18) і (19), звідки отримаємо :

(20)

Тому в кінцевому вигляді формули (17) будуть записані так:

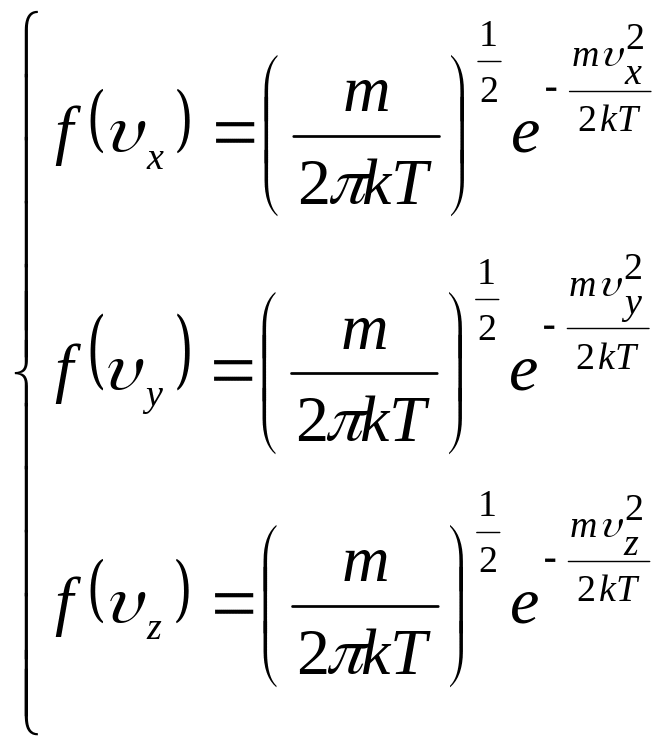
(21)

Т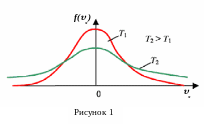 аким чином, ми отримали функції розподілу молекул за компонентами швидкості , тобто за величиною і за напрямками ( задано в напрямку осі x, – осі y, – осі z). Графік функції розподілу молекул зображений на рис. 1. Легко побачити, що розподіл симетричний відносно початку координат і має максимум при проекції швидкості _x = 0. З підвищенням температури частка таких молекул зменшується Позитивні і негативні значення _x мають однакову імовірність, тому найбільш ймовірна проекція і середня проекція швидкості дорівнюють нулеві .

Згідно (5):

W (x, y, z) = xyz dx dy dz

Підставимо в цю формулу значення x,yi z з (21):

W (x, y, z) = (22)

Оскільки , отримаємо:

W (x, y, z) = (23)

Ця формула показує, скільки молекул з усіх, що знаходяться в об’ємі, мають швидкості, координатні складові яких лежать в межах від x до x + dx, від y до y + dy, від z до z + dz, тобто поблизу визначеного вектора швидкості із заданим напрямком і величиною.

Перейдемо від розподілу проекцій швидкості (23) до розподілу модуля швидкості. Для цього вводиться поняття простору швидкостей та сферичні координати, що призводить до заміни у формулі (23) dx dy dz на V, або :

(27)

Формула (27) являє собою закон Максвела розподілу молекул за абсолютними значеннями швидкостей. Нагадаємо ще раз, що величина W дає нам ймовірність того, що величина швидкості будь-якої молекули газу має значення в інтервалі від  до  + d.

Оскільки W = d, то:

  = (28)

де  – це функція розподілу молекул за швидкостями. Вона визначає долю молекул одиниці об’єму газу, швидкості яких знаходяться в одиничному інтервалі швидкостей, що включає в себе і дану швидкість.

Крім функції розподілу за абсолютними значеннями швидкості використовують функцію розподілу за значеннями кінетичної енергії поступального руху молекул Е_к. Для цього перейдемо від змінної  до змінної . Зробимо заміну в (27):

, ,

т оді

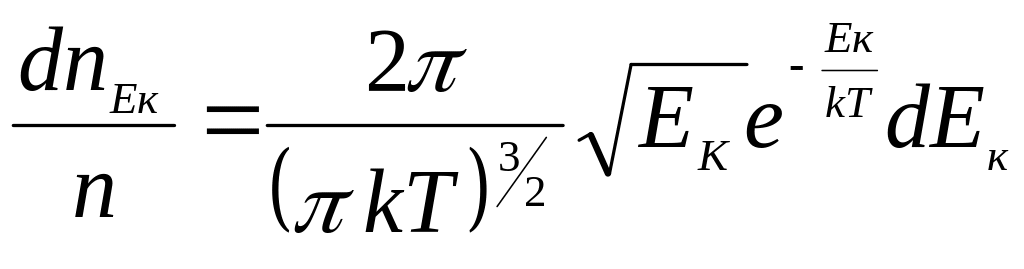(29)

де - визначає число молекул, кінетична енергія поступального руху яких має значення в інтервалі від Е_к до Е_к+dЕ_к. Тоді функція розподілу за значеннями кінетичної енергії

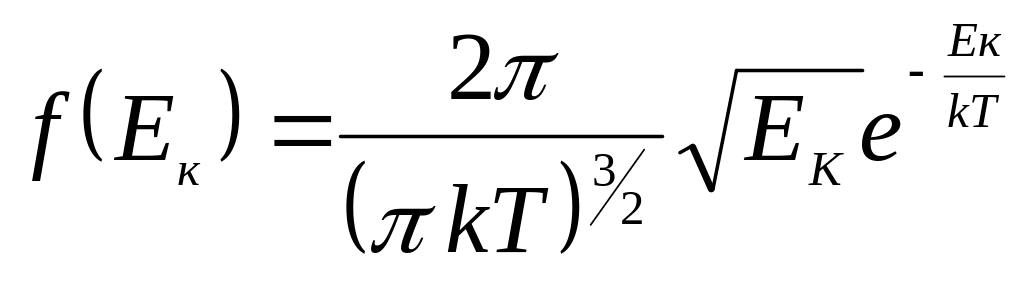
(30)