10. Декомпозиція задач за вихідними даними.

Процес розподілу обчислень на менші частини, деякі або всі з яких можуть бути виконані паралельно, називається декомпозицією.

Застосовується до даних, які оперують великими масивами чисел. Проводиться в два етапи:

2. розділення даних

3. використання для розподілу основного завдання на окремі задачі цього розділення

Часто застосовуваний спосіб для виявлення паралелізму в задачах, які оперують великими задачами. 2 етапи:

• дані над якими виконується обчислення розділяються

• попереднє секціонування використовується для розбиття на окремі задачі. Як правило ці задачі є подібними.

Декомпозиція за даними буває декількох типів:

• за вихідними даними – такий тип розподілу задач можливий, коли кожний вихідний елемент може бути обчислений як функція входу не залежно від решти вихідних елементів. Приклад матричного множення

| A₁₁ A₁₂| * | B₁₁ B₁₂| = | C₁₁ C₁₂|

| A₂₁ A₂₂| * | B₂₁ B₂₂| | C₁₁ C₁₂|

• розподіл за вхідними даними. Він може бути здійснений лише в тому випадку, якщо кожен вихідний результат є функцією від вхідних даних, але секціонування з вхідними даними неможливе. Приклад: знаходження мінімуму, максимуму функції.

• Декомпозиція за проміжними даними.визначаються як багатоступінчасті обчислення, результат одного завдання є входу до решти, зазвичай призводять до більш високого ступеня розпаралелювання, але частіш за все не існують. Розглянемо повторно приклад матричного множення:

| A_11|| * | B₁₁ B₁₂|

| A₂₁|

… = | C₁₁ C₁₂|

| A₁₂| * | B₂₁ B₂₂| | C₁₁ C₁₂|

|A₂₂|

Правило власника обчислень – кожне секціонування має виконувати обчислення над всіма даними, якими володіє.

Секціонування за вихідними даними – такий тип секціонування можливий, коли вихідні дані не залежать один від одного і кожен вихідний елемент є лише функцією входу

Приклад: матричне множення. Обчислення кожного вихідного елементу виділяється в окрему задачу.

11. Дослідницька декомпозиція задач.

Вона використовується, щоб секціонувати завдання, які передбачають декілька шляхів знаходження розв‘язку (існує простір для рішень). Приклад «задача 15». Задача типово розв’язується використовуючи методи пошуку дерева, набір просторових конфігурацій можна розглядати як граф, кожен вузол графа – це конфігурація, а ребра сполучають конфігурації, які можуть бути отримані єдиним рухом клітинки.

1	2	3	4
5	6	7	8
9	10		12
13	14	11	15

1	2	3	4
5	6	7	8
9	10		12
13	14	11	15

1	2	3	4
5	6		8
9	10	7	12
13	14	11	15

1	2	3	4
5	6	7	8
9		10	12
13	14	11	15

…

…

1	2	3	4
5	6	7	8
9	10	11	12
13	14		15

…

Аномальні прискорення.

Tпар=м Апар=4м tпар=1

Tпосл=м Апосл=м tпосл=3м+1

Апар=4; Апосл=3м

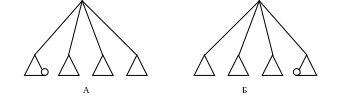
Перевагою дослідницькій декомпозиції є у пришвидшенні знаходження результату порівняно із послідовним алгоритму, хоча іноді взалежності від локалізації результату, час роботи між паралельним і послідовним алгоритмом буде однаковим, а об’єм роботи буде більшим.

Недолік: надлишкова завантаженість апаратної частини, оскільки лише одна гілка принесе вірний результат.