2.1.3. Метод релаксации

Прежде чем излагать метод релаксации, рассмотрим вопросы терминологии. Слово "релаксация" (ослабление) часто употребля­ется для определения класса итерационных алгоритмов при реше­нии систем линейных уравнений. Этот класс методов характери­зуется последовательным сведением к нулю наихудшего из остат­ков, соответствующего какому-либо линейному уравнению. Сущест­вует несколько методов релаксации: координатная, блочная, груп­повая и сверхрелаксация. Последнее определение применяется к такому релаксационному процессу, когда вместо полной ликвидации остатка в одном из уравнений осуществляется уменьшение абсолютного значения этого остатка.

В некоторых случаях под релаксацией понимают область ис­кусства по решению систем линейных уравнений с привлечением различных вычислительных приемов.

В ряде работ по нелинейному программированию под релакса­цией подразумеваются методы решения экстремальных задач, обеспечивающие максимализацию целевой функции.

В дальнейшем будем придерживаться следующего определения метода релаксации, имеющего наибольшее распространение при современном изложении нелинейного программирования: "метод, при котором следующая точка отличается от текущей значением только одной компоненты, называется релаксационным" [3]. Данное определение наиболее удачно отражает характерные черты тех ре­лаксационных методов, которые успешно применялись при решении систем линейных уравнений еще со времен Гаусса.

Последовательность вычислений для случая двух переменных методом релаксации, основанном на покоординатной минимизации критериальной функции, состоит в следующем:

1. В точке Р(х₁, х₂) с координатами, равными средне­му арифметическому из координат исходных пунктов, вычисляем значение целевой функции Ф_j, полагая j = 1.

2. Учитывая опыт работы, задаем начальное значение шага релаксации l_j = S_ср. / 3, где S_ср. ¾ средняя длина стороны в геодезической сети.

3. Вычислим значения целевой функции в четырех точках релаксации , , и найдем из этих значений наименьшее Ф_min.

4. Если Ф_j £ Ф_min, то l_j уменьшают вдвое и возвращаются к п.3, предусматривая регулировку шага релаксации по принципу дихотомии.

5. От точки Р_j перейдем к точке Р_i (i = 1, 2, 3, 4) с наименьшим значением целевой функции. В результате получим но­вую точку 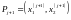для следующего приближе­ния и, полагая Ф_j £ Ф_min, переходим к п.3. Приближения прекращают, если l_j+1 не окажется меньшим ранее заданного значения.:

Траектория минимизации по методу релаксации изображена на рис. 2.4.

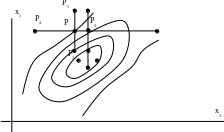Р ис.2.4. Траектория минимизации по методу релаксации.

Наиболее существенный недостаток методов покоординатной минимизации (Гаусса-Зейделя, релаксации и др.) заключается в следующем. Предположим, что изолинии (изоповерхности) целевой функции представляют собой эллипсы (гиперэллипсоиды) с экс­центриситетом, близким к единице. Тогда, если большая полуось эллипса образует угол с направлениями координатных осей, близкий к p/4 итерации сходятся очень медленно. Механизм этого явления состоит в преждевременном уменьшении длины шага на пу­ти к точке экстремума. Примером может служить траектория мини­мизации, изображенная на рис.2.4. При j > 5 шаг l_j будет постоянно уменьшаться для обеспечения минимизации целевой функции. В связи с этим в последнее время наблюдается значи­тельный интерес к комбинированным методам нелинейного программирования. с использованием на заключительных этапах метода Ньютона.