Время вычислений на эвм можно предрассчитать по формуле

,

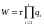где t ¾ время, необходимое для вычисления целевой функции в одном узле регулярной сетки; t ¾ число неизвестных координат (число параметров); q ¾ число узлов сетки по одной пере­менной.

Например, для вычисления на ПЭВМ 1ВМ РС/АТ-286 при t = 4, q_i = 10 требуется 12 с машинного времени. Для определения координат двух пунктов в пространстве при тех же условиях пот­ребуется 2 мин машинного времени, что достаточно много. Однако такие случаи редко возникают на практике. И, если они встречают­ся, то можно задать предварительные координаты со схемы или карты с точностью S_min/3, где S_min ¾ наименьшая длина стороны между исходным и определяемым пунктами.

Достоинство слепого поиска по сравнению со всеми другими методами минимизации состоит в том, что он позволяет находить не только все локальные экстремумы целевой функции произвольного вида, но и глобальный экстремум.

После определения методом слепого поиска узла сетки, расположенного в окрестности глобального минимума, обычно продолжают минимизацию целевой функции другим, наиболее рациональным мето­дом нелинейного программирования.

Среди методов прямого поиска широкое применение в практике геодезических вычислительных работ получил алгоритм Гаусса-Зейделя. В нелинейном случае уравнивания геодезических сетей этот метод применили Г.М.Гринберг [25], З.М.Юршанский [108] и др.

Метод Гаусса-Зейделя обладает простой стратегией поиска экстремума, легко программируется, однако во многих случаях ус­тупает по скорости сходимости другим методам прямого поиска, например, методу Хука и Дживса, Нелдера-Мида (поиску по дефор­мированному многограннику) и Пауэлла [39]. Последний метод применил для геодезических целей З.Адамчевский [110]. Последо­вательность вычислений в методе Пауэлла в модификации З.Адамчевского состоит в следующем.

1. В области притяжения точки минимума выбирают произволь­ную точку Р₀ и вычисляют в ней значение целевой функции – Ф₀.

2. Находят длину шага интерполяции по заранее полученной эмпирической формуле

Здесь важно отметить, что l_j зависит от значений целевой функции и поэтому уменьшается при переходе от одного прибли­жения к другому.

3. По одному из координатных направлений выполняют одномер­ную квадратичную интерполяцию. Для этого по значениям целевой функции в двух вспомогательных точках Р₁ и Р₂ (рис.2.3) вычисляют коэффициент

и находят координаты точки

;

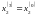
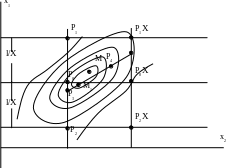
Рис. 2.3. Минимизация целевой функции по методу Пауэлла.

4. По коэффициенту d вычисляют интерполированное зна­чение целевой функции в точке Р₃

.

5. Повторяют вычисления, изложенные в пп. 3 и 4, для дру­гого направления, параллельного к начальному, находят коорди­наты точки 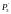и значение целевой функции в этой точке ¾ .

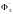6. По координатам точки Р₄ лежащей на средине отрезка 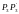вычисляют Ф₄.

7. Выполняя квадратичную интерполяцию по Ф₃, и Ф₄ находят точку и заканчивают первое приближение.

8. Весь вычислительный процесс повторяют с п.2 по локали­зации достаточно малой окрестности минимума.

Как показали исследования, опубликованные в [34, 103, 105], метод Пауэлла имеет более высокую сходимость по сравнению с другими методами минимизации для гладких и всюду выпуклых целевых функций. Особенно это заметно на примерах решения линей­ных засечек, приведенных З.Адамчевеким [97]. В случае решения комбинированных линейно-угловых засечек, то есть тогда, когда целевая функция может иметь сложную форму изолиний, эффектив­ность метода снижается.

Основная причина заключается в отсутствии регулировки шага минимизации с учетом особенностей строения целевой функ­ции. В этом отношении могут оказаться полезными методы релак­сации, предусматривающими регулировку длины шага l между приближениями. .