Глава 2

ВЫЧИСЛЕНИЕ ПРЕДВАРИТЕЛЬНЫХ КООРДИНАТ ПУНКТОВ МЕТОДАМИ НЕЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ

2.1. Методы нелинейного программирования, используемые в геодезических вычислениях

2.1.1. Градиентные методы

При решении задач оптимизации применяют различные итера­ционные методы, обеспечивающие процесс минимизации целевой функции согласно неравенству

,

где j - номер приближения.

Большой класс задач оптимизации успешно решается гради­ентными методами спуска, предусматривающими итерационный про­цесс

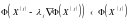, lj > 0, (2.1)

где lj - шаг минимизации в направлении, противоположном градиенту

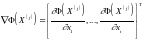, (2.2)

Из-за сложной формы гиперповерхностей Ф(Х) = const направление, противоположное градиенту, в общем случае не ориентировано на точку минимума. Поэтому необходим итерацион­ный прогресс.

Градиентные методы поиска экстремума различаются в основ­ном способом выбора шага lj, что предопределяет объем вычислений на каждой итерации. Требования к выбору шага миними­зации имеют некоторые противоречия. Во-первых, шаги lj должны быть достаточно малыми, чтобы выполнялось неравенство (2.1) и вместо спуска не начался подъем. Во-вторых, если шаги окажутся слишком малыми, то резко возрастет объем вычислений и снизится эффективность используемого алгоритма.

Поиск минимума с малым постоянным шагом выполняется гра­диентным методом, в котором после каждого шага заново опреде­ляется направление градиента и осуществляется следующий малый шаг. Графическая интерпретация метода градиента для двух переменных х1 и х2 дана на рис. 2.1, где изображены изолинии целевой функции и траектория спуска от начальной точки Р к точке минимума М .

х₂

Р ис. 2.1. Траектория минимизации методом градиента

Минимизация целевой функции с использованием наибольшего возможного шага в направлении, противоположном градиенту, осу­ществляется методом скорейшего спуска. В зависимости от спо­соба вычисления длины шага минимизации применяются различные модификации метода наискорейшего спуска.

Классическим, но редко применяемым на практике, является способ, основанный на определений шага lj из уравнения

с использованием разложений целевой функции в ряд Тейлора.

Наибольшее распространение на практике получили различные модификации метода наискорейшего спуска, основанные на одно­мерной минимизации критериальной функции в направлении скорей­шего ее уменьшения. При этом применяются различные однопараметрические алгоритмы минимизации: метод золотого сечения, поиск Фибоначчи, метод квадратичных приближений и др. [103]. После­довательность минимизации целевой функции для случая двух переменных модифицированным методом спуска состоит в следующем.

1. Вычислим значение критериальной функции в начальной точке, которое обозначим .

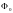2. Найдем частные производные 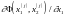и .

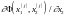3. Вычислим длину шага минимизации по формуле

,

где квадрат евклидовой нормы градиента найдем из выражения

.

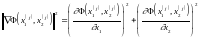4. Определим координаты двух вспомогательных точек

;

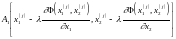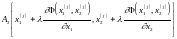
и вычислим в этих точках значения целевой функции, обозначая их соответственно и

5. По величинам , , выполним квадратичную интерполяцию. В результате получим коэффициент

.

Если 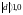, l удваивают, и повторяют вычисления с п.4, чтобы не допустить экстраполяции. Если 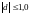, то находят новую длину шага .

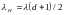6. Вычислим координаты точки для следующего приближения

;

,

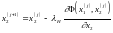и найдем в ней значение целевой функции.

7. Если 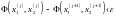, где e ¾ некоторое малое заранее заданное положительное число, то приближения прекращают. В противном случае, продолжают вычисления с п.1.

Наиболее существенные осложнения при применении метода скорейшего спуска возникают тогда, когда процесс приближений выполняется в окрестности минимума. Здесь траектория минимиза­ции начинает изменяться скачками, как показано на рис.2.2, что для достижения необходимой точности приводит к большому числу приближений.