3. Сфера

Сферою називають поверхню, утворену обертанням кола або півкола навколо свого діаметру. Точка, рівновіддалена від усіх точок сфери, називається центром сфери. Відрізок, що сполучає центр сфери з її довільною точкою, називається радіусом сфери.

Візьмемо в просторі прямокутну систему координат Oxyz. Щоб скласти рівняння сфери з центром у точці і радіусом R (рис. 8), візьмемо в просторі довільну точку . Точка М належить сфері тоді і лише тоді, коли , або . Це і є рівняння сфери. Для зручності його записують у такому вигляді:

. (6)

Зокрема, якщо центр сфери збігається з початком координат, тобто , то рівняння такої сфери має вигляд

.

Якщо в рівнянні (12.6) розкриємо дужки, то матимемо загальне рівняння сфери

, (7)

де , , , .

Це рівняння має такі властивості.

1. Рівняння (7) є рівнянням другого ступеня відносно х, у і z, отже, сфера – поверхня другого порядку.

2. Коефіцієнти при , , рівні між собою.

3. У рівнянні відсутні члени з добутками , , .

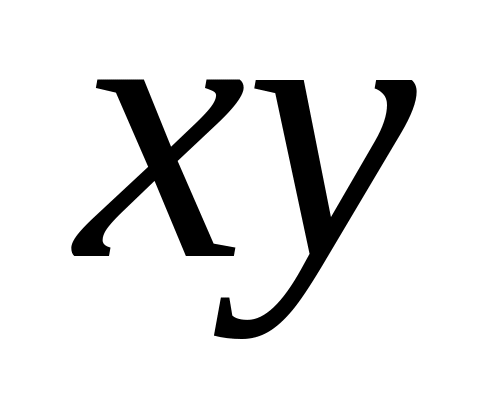Проте не всяке рівняння виду (7), яке задовольняє умови 1-3, зображає сферу.

Приклади. 6. Знайти центр і радіус сфери, заданої рівнянням .

 Виділяючи повні квадрати по х, у і z, запишемо задане рівняння у вигляді . Отже, точка – центр сфери і – її радіус. 

7. Скласти рівняння сфери, яка проходить через точки , і , якщо її центр знаходиться в площині Оху.

 Так як точки А, В і С належать сфері , у якої центр знаходиться у площині Оху (звідки , то їхні координати повинні обертати шукане рівняння в тотожність; тому отримуємо рівняння

, , .

Звідси

, ,

або

, тобто ;

, тобто ;

Отже, , . Значить, центр сфери – точка .

Далі знаходимо . Таким чином, шукане рівняння має вигляд

. 

8. Знайти координати центра і радіус кола

 Із центра сфери опустимо на площину перпендикуляр, рівняння якого можна записати у вигляді

(*)

(в якості напрямного вектора цього перпендикуляра можна взяти нормальний вектор заданої площини).

Тепер знайдемо координати точки перетину прямої (*) з площиною . Ця точка і є центр кола, що є перерізом сфери даною площиною.

Записавши рівняння прямої в параметричному вигляді: , , і підставивши х, у, z, в рівняння площині, отримаємо

, тобто .

Отже, , , , тобто центр кола знаходиться в точці .

Знайдемо тепер відстань d від центра сфери до площини :

.

Радіус кола r визначиться із рівняння , де R – радіус сфери; таким чином, , тобто .

4. еліпсоїд

Еліпсоїдом називається поверхня, яка в деякій прямокутній системі координат визначається рівнянням

, (8)

де a, b, c – додатні числа. Величини а, b, c називаються півосями еліпсоїда. Якщо будь-які дві півосі рівні між собою, то триосний еліпсоїд перетворюється в еліпсоїд обертання, а якщо всі три півосі рівні між собою, – у сферу.

Рівняння (8) називається канонічним рівнянням еліпсоїда. Дослідження форми еліпсоїда проведемо методом паралельних перерізів. Для цього розглянемо перерізи даного еліпсоїда площинами, паралельними площині Oxy. Кожна з таких площин визначається рівнянням , де h – довільне дійсне число, а лінія, яка утворюється в перерізі, визначається рівнянням

; . (9)

Дослідимо рівняння (12.9) при різних значеннях h.

1. Якщо , , то і рівняння (9) ніякої лінії не визначають, тобто точок перетину площини з еліпсоїдом не існує.

2. Якщо , то і лінія (12.9) вироджується в точки і , тобто площини і дотикаються до еліпсоїда.

3. Якщо , то , де , , тобто площина перетинає еліпсоїд по еліпсу з півосями і . При зменшенні h значення і збільшуються і досягають своїх найбільших значень при , тобто в перерізі еліпсоїда площиною Oxy матимемо найбільший еліпс з півосями , .

А налогічні результати дістанемо, якщо розглядатимемо перерізи еліпсоїда площинами і .

Таким чином, розглянуті перерізи дають змогу зобразити еліпсоїд як замкнуту овальну поверхню (рис. 9).

Приклад. 9. Знайти центр і півосі еліпсоїда, заданого рівнянням

.

 Виділяючи повні квадрати по х, у, z, дістанемо або . Отже, даний еліпсоїд має півосі: , , ; його центр знаходиться в точці . 