1. Поняття поверхні другого порядку

Поверхнею другого порядку називається множина точок, прямокутні координати яких задовольняють рівняння виду

, (1)

де принаймні один з коефіцієнтів А, В, С, D, E, F відмінний від нуля.

Рівняння (12.1) називається загальним рівнянням поверхні другого порядку.

Поверхня другого порядку як геометричний об’єкт не змінюється, якщо від заданої прямокутної системи координат перейти до іншої. При цьому рівняння (12.1) і рівняння, знайдене після перетворення координат, будуть еквівалентними.

Можна довести, що існує система координат, в якій рівняння (1) має найпростіший (або канонічний) вигляд.

Рівняння (1) визначає не лише поверхні другого порядку, але ще і сукупність двох площин, пряму, точку, а може, взагалі не мати геометричного змісту (тобто визначати „уявну” поверхню). Для встановлення, яку фігуру визначає рівняння (12.1) іноді буває достатньо елементарних перетворень (згрупувати доданки, помножити або поділити рівняння на число тощо).

Приклад.1. Який геометричний зміст мають рівняння:

1) ;

2) ;

3) .

 1) дане рівняння можна записати у вигляді і розкласти ліву частину на множники: , отже, дане рівняння визначає сукупність двох площин і ;

2) помноживши на 2, перепишемо рівняння у такому вигляді або ; це рівняння задовольняють координати лише тих точок, для яких виконуються рівності , , , таким чином, дане рівняння визначає пряму ;

3) перепишемо рівняння у вигляді , очевидно, що це рівняння не має геометричного змісту, так як ліва частина рівняння ні при яких дійсних значеннях змінних х, у, z не може бути від’ємною величиною. 

До поверхонь другого порядку належать, зокрема, циліндричні та конічні поверхні, поверхні обертання, сфера, еліпсоїд, однопорожнинний та двопорожнинний гіперболоїди, еліптичний та гіперболічний параболоїди. Розглянемо ці поверхні та їхні канонічні рівняння.

2. Класи поверхонь

В залежності від того, яким чином утворена дана поверхня, виділяють класи поверхонь. Основним із методів дослідження форми поверхонь вважають метод паралельних перерізів, який полягає в тому, що дану поверхню перетинають площинами, паралельними координатним площинам, і в залежності від того, які фігури одержуються, роблять висновок про загальний вигляд всієї поверхні.

2.1. Циліндричні поверхні

Ц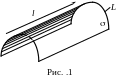 иліндричною поверхнею називають поверхню , утворену множиною прямих (твірних), які перетинають задану лінію L (напрямну) і паралельні заданій прямій l (рис. 1). Вивчатимемо лише такі циліндричні поверхні, напрямні яких лежать в одній з координатних площин, а твірні паралельні координатній осі, яка перпендикулярна до цієї площині.

Розглянемо випадок, коли твірні циліндричної поверхні паралельні осі Oz, а напрямна лежить в площині Оху.

Нехай задано рівняння

, (2)

я ке в площині Оху визначає (рис.2) деяку лінію L – множину точок , координати яких задовольняють це рівняння. Дане рівняння задовольняють також координати всіх тих точок простору, у яких дві перші координати х і у збігаються з координатами будь-якої точки лінії L, а третя координата z – довільна, тобто тих точок простору, які проектуються на площину Оху в точки лінії L.

Всі такі точки лежать на прямій, яка паралельна осі Оz і перетинає лінію L в точці . Сукупність таких прямих і є циліндричною поверхнею .

Якщо точка не лежить на поверхні , то вона не може проектуватися в точку лінії L, тобто координати такої точки рівняння (2) не задовольняють. Отже, рівняння (2) визначає поверхню . Таким чином, рівняння визначає в просторі циліндричну поверхню, твірні якої паралельні осі Оz, а напрямна L в площині Оху задається тим самим рівнянням . Ця сама лінія у просторі Охуz задається двома рівняннями:

Аналогічно рівняння , в якому відсутня зміна у, визначає в просторі циліндричну поверхню, твірні якої паралельні осі Оу, а напрямна L в площині Охz задається тим самим рівнянням ; рівняння визначає в просторі циліндричну поверхню, твірні якої паралельні осі Ох.

Циліндричні поверхні можна класифікувати в залежності від того, яка лінія є її напрямною:

• якщо напрямною в площині Оху є коло , то циліндрична поверхня, яка визначається рівнянням , називається прямим круговим циліндром, її твірні паралельні до осі Oz (рис. 3, а);

• якщо напрямною в площині Оху є еліпс , то циліндрична поверхня, яка визначається рівнянням , називається еліптичним циліндром (рис. 3, б);

• якщо напрямною в площині Оху є гіпербола , то циліндрична поверхня, яка визначається рівнянням , називається гіперболічним циліндром (рис. 3, в);

• якщо напрямною в площині Оху є парабола , то циліндрична поверхня, яка визначається рівнянням , називається параболічним циліндром (рис.3, г).

Рис. 3

Приклад. 2. Яку поверхню визначають в просторі рівняння:

1) ;

2) .

 1) рівняння визначає в просторі параболічний циліндр, напрямна якого в площині Oуz є парабола , а твірні паралельні осі Ох (рис. 12.3, д);

2) рівняння може бути представлено у вигляді і розпадається на два рівняння: і , тобто воно визначає дві площини – площину Оху і бісектральну площину , що проходить через вісь ординат. 

Зауваження. Слід пам’ятати, що криву в просторі можна задати або параметрично, або у вигляді лінії перетину двох поверхонь. Наприклад, рівняння напрямної еліптичного циліндра, тобто еліпса в площині Оху мають вигляд