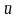- •Введение
- •2. Система цифровой связи
- •3. Исходные данные
- •3.1. Источник сообщения
- •3.2. Аналого-цифровой преобразователь
- •3.3. Кодер
- •3.4. Формирователь модулирующих символов
- •3.5. Модулятор
- •3.6. Непрерывный канал
- •3.7. Демодулятор
- •Определить среднюю вероятность ошибки на выходе преобразователя.
- •3.8. Декодер
- •4. Список использованной литературы
- •3.1. Источник сообщения 6
- •3.4. Формирователь модулирующих символов 17
- •3.5. Модулятор 22
3.3. Кодер
Используется помехоустойчивый сверточный код. Выбрать структурную схему сверточного кодера в [7].
Вариант 81 100000001
1. Задать следующие параметры сверточного кодера:
степень
кодирования
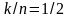 ;
;
длину
кодового ограничения
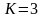 ;
;
векторы
связи
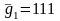 и
и
 ;
;
импульсная
характеристика
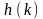 задается информационной последовательностью
111011000…, где
– номер тактового интервала. В [7]
импульсная характеристика обозначена
задается информационной последовательностью
111011000…, где
– номер тактового интервала. В [7]
импульсная характеристика обозначена
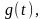 а в КР используем обозначение
а в КР используем обозначение
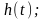
кодовое
расстояние
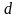 .
.
Расчет:
2. В [7] определить и изобразить структурную схему кодера, соответствующую заданным параметрам.

Рис. 3.3.1. структурная схема сверточного кодера
3.
Изобразить решетчатую диаграмму
сверточного кодера от момента времени
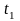 до момента времени
до момента времени
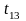 .
Решетчатая диаграмма строится аналогично
диаграмме на рис. 9 в [7, с. 21].
.
Решетчатая диаграмма строится аналогично
диаграмме на рис. 9 в [7, с. 21].
Нарисуем граф переходов рис. 3.3.2:

Рис. 3.3.2. граф переходов
Согласно графу переходов рисуем решетчатую диаграмму рис. 3.3.3.

рис. 3.3.3. решетчатая диаграмма.
4.
По решетчатой диаграмме сверточного
кодера определить последовательность
кодовых символов (КС)
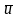 на выходе кодера при условии, когда на
вход кодера поступает 9-разрядная
двоичная последовательность информационных
символов (ИС)
на выходе кодера при условии, когда на
вход кодера поступает 9-разрядная
двоичная последовательность информационных
символов (ИС)
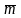 ,
соответствующая заданному уровню
квантования
(разд. 3.2, п. 6).
,
соответствующая заданному уровню
квантования
(разд. 3.2, п. 6).
Информационные
символы (ИС)
|
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
Кодовые символы
(КС)
|
11 |
10 |
11 |
00 |
00 |
00 |
00 |
00 |
11 |
3.4. Формирователь модулирующих символов
Решение:
Изобразить сигнальное созвездие для вида модуляции – КАМ-16 (квадратурная амплитудная модуляция) рис. 3.4.1..

Рис. 3.4.1. КАМ-16
Изобразить график реализации
 случайного процесса
случайного процесса
 с выхода блока сверточного кодера (К)
на входе блока ФМС на первых 16 бинарных
интервалах длительностью
с выхода блока сверточного кодера (К)
на входе блока ФМС на первых 16 бинарных
интервалах длительностью
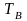 .
Написать аналитическое выражение для
случайного процесса
.
.
Написать аналитическое выражение для
случайного процесса
.
В соответствии с сигнальным созвездием модулятора КФМ-4 изобразить для входной реализации графики реализаций
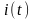 и
и
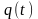 на выходе блока ФМС случайных процессов
на выходе блока ФМС случайных процессов
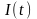 и
и
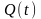 на символьных интервалах длительностью
на символьных интервалах длительностью
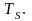 Написать аналитические выражения для
случайных процессов
и
Написать аналитические выражения для
случайных процессов
и
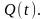
Реализацию случайного процесса
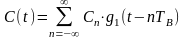
можно представить в следующей аналитической форме
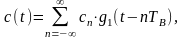
где
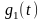 – прямоугольный импульс длительностью
,
– прямоугольный импульс длительностью
,
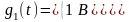

где
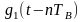 – прямоугольный импульс такой же формы,
как
,
но сдвинутый вправо
относительно импульса
на величину
– прямоугольный импульс такой же формы,
как
,
но сдвинутый вправо
относительно импульса
на величину
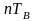 ,
если
,
если
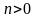 ,
или влево,
если
,
или влево,
если
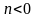 ;
;
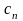 – численный коэффициент, являющийся
реализацией случайной величины
– численный коэффициент, являющийся
реализацией случайной величины
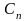 на
на
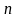 -интервале
.
-интервале
.
Последовательность КС из 16 символов: 1011 0000 0000 0011
Процессы и можно представить в виде
 ;
;
 ,
,
где
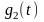 – прямоугольный импульс длительностью
– прямоугольный импульс длительностью
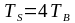 (рис. 3.4.2., б);
(рис. 3.4.2., б);
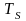 – символьный интервал;
– бинарный интервал.
– символьный интервал;
– бинарный интервал.
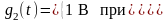
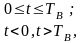
где
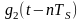 – прямоугольный импульс такой же формы,
как импульс
,
но сдвинутый вправо относительно
импульса
на величину nTs,
если
,
или влево, если
;
– прямоугольный импульс такой же формы,
как импульс
,
но сдвинутый вправо относительно
импульса
на величину nTs,
если
,
или влево, если
;
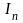 и
и
 – независимые случайные величины,
заданные на символьном интервале с
номером
,
которые согласно сигнальному созвездию
(рис. 3.4.1) принимают два дискретных
значения
– независимые случайные величины,
заданные на символьном интервале с
номером
,
которые согласно сигнальному созвездию
(рис. 3.4.1) принимают два дискретных
значения
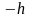 ,
,
 ,
3h,
-3h
с вероятностью 0,25 каждое, т.е.
,
3h,
-3h
с вероятностью 0,25 каждое, т.е.
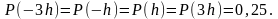

Рис. 3.4.2. Реализации и случайных процессов и
для КАМ-16
Написать аналитические выражения для корреляционной функции
 и спектральной плотности мощности
и спектральной плотности мощности
 входного случайного процесса
и построить графики этих функций.
входного случайного процесса
и построить графики этих функций.

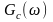 =
=
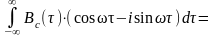
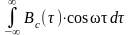 .
.
Написать аналитические выражения для корреляционных функций
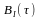 и
и
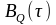 ,
спектральных плотностей мощности
,
спектральных плотностей мощности
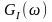 и
и
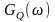 случайных процессов
и
случайных процессов
и
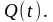 Построить графики этих функций.
Построить графики этих функций.
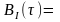
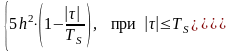
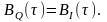
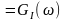
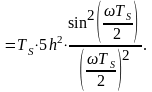

Рис.
3.4.3. график корреляционной функции
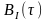

Рис. 3.4.4. график функции спектральной мощности
Сравнить графики корреляционных функций и спектральных плотностей мощности сигналов на входе и выходе блока ФМС. Привести краткое описание результатов сравнения и, используя общие положения теории преобразования Фурье, пояснить, почему спектр выходных сигналов уже спектра входного сигнала.
Теорема Хинчина — Колмогорова (также известная как Теорема Винера — Хинчина и иногда как Теорема Винера — Хинчина — Эйнштейна) утверждает, что спектральной плотностью мощности стационарного в широком смысле случайного процесса является преобразование Фурье соответствующей автокорреляционной функции
Теорема удобна для анализа линейных стационарных систем, где входные и выходные значения не интегрируемы в квадратурах, из-за чего преобразований Фурье не существует. Как следствие, преобразование Фурье автокорреляционной функции выходного сигнала ЛСС-системы равно произведению преобразования Фурье автокорреляционной функции входного сигнала системы на квадрат модуля преобразования Фурье её импульсной характеристики. Это выполняется даже когда преобразований Фурье входных и выходных сигналов не существует, из-за того что они не интегрируемы. Поэтому входные и выходные параметры не могут быть прямо связаны преобразованием Фурье импульсной передаточной функции.
Из того, что преобразование Фурье автокорреляционной функции сигнала есть спектр мощности сигнала, следует, что спектр мощности выходного сигнала равен произведению спектра мощности входного и передаточной функции системы.
Это следствие используется в нахождении спектра мощности параметрическим методом.