МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ
Національний університет «Львівська політехніка»
Апроксимація функцій
Метод найменших квадратів
Завдання та методичні рекомендації
до лабораторної роботи № 7
з курсу «Чисельні методи»
для базового напрямку 040204 «Прикладна фізика»
Затверджено
на засіданні кафедри
обчислювальної математики та програмування
Протокол № 5 від 30.01.2012 p.
ЛЬВІВ – 2011
Апроксимація функцій. Метод найменших квадратів. Завдання та методичні рекомендації до лабораторної роботи № 7 з курсу «Чисельні методи» для базового напрямку 040204 «Прикладна фізика» / Укл. Я.М.Глинський, Н.М.Гоблик, З.О.Гошко, В.А.Ряжська, 2012. – 12 с.
Укладачі: Глинський Я.М., канд. фіз.-мат. наук, доц.
Гоблик Н.М., ст. викл.
Гошко З.О., асистент
Ряжська В.А., канд. фіз.-мат. наук, доц.
Відповідальна за випуск Ряжська В.А., канд. фіз.-мат. наук, доц.
Рецензент доктор фіз.-мат. наук, проф. Чабанюк Я.М.
Передмова
У методичних вказівках для заданої таблично функції розглянуто метод побудови аналітичної апроксимаційної функції, яка найкращим чином наближає задані дані.
Методичні вказівки містять короткі теоретичні відомості, приклад побудови лінійного та квадратичного многочленів для заданої таблично функції, обчислення їх похибки у заданих точках, а також індивідуальні завдання для самостійної роботи студентів. Приклад розв’язаний як вручну, так і у середовищі MatLab
Методичні вказівки призначені для студентів базового напрямку 040204 «Прикладна фізика» і укладені відповідно до робочої програми курсу «Чисельні методи».
1. Мета роботи
Мета роботи – для заданої таблично функції побудувати апроксимаційну функцію, яка найкращим чином наближає експериментальні дані.
2. Теоретичні відомості
Нехай
у точках
відомо значення
деякої
невідомої функції
.
Орієнтовний
вигляд графіка функції можна визначити,
побудовавши у площині графік за заданими
точками. Потрібно
знайти аналітичний вигляд функції, яка
залежить від
параметрів
,
причому функція у = 
має «досить добре» наближувати функцію
на всьому проміжку
.
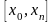Метод найменших квадратів розв’язування системи полягає у тому, щоб визначити невідомі, які мінімізують суму вигляду
.
З умови мінімуму
величин S
як функції від
дістаємо систему лінійних алгебраїчних
рівнянь
.
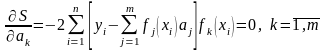Розв’язок системи m лінійних алгебраїчних рівнянь з m невідомими вважаємо наближеним розв’язком системи.
Приклад. Методом найменших квадратів для функції заданої таблицею
|
0,00 |
0,25 |
0,50 |
0,75 |
1,00 |
|
1 |
2 |
1 |
0 |
1 |
побудувати лінійний і квадратичний многочлени.
Для наближення функції використаємо лінійний многочлен
.
Тоді
.
Необхідна умова
мінімуму функції
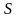– виконання співвідношень
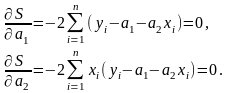
Згрупувавши разом
коефіцієнти при
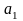і
,
отримаємо систему двох лінійних рівнянь
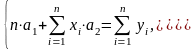
Обчислимо відомі значення
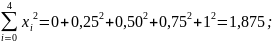
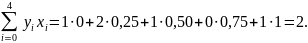
та підставимо їх у систему. Отримаємо
Розв’язавши
систему одним з відомих методів, отримаємо
і
.
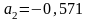Отже, шуканий лінійний многочлен, який наближає наші експериментальні дані, має вигляд
.
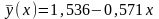Розв’язання в середовищі MATLAB.
Апроксимуючу функцію шукаємо у вигляді P(x,a,b)=ax+b
Знаходимо похідні за a, та за b:
Записуємо систему рівнянь виду (2):
(3)
Розкриємо дужки:
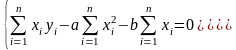(4)
Розділемо на n і перенесемо вправо доданки, які не залежать від a,b:
(5)
Введемо позначення і перепишемо систему (5) в матричному вигляді:
(6)
де:
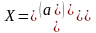
Матричне рівняння (6) можна розв'язати в MATLAB:
function coef=apr(x,y)
%лінійна апроксимація y=ax+b
%X –вектор значень аргумента
%У –вектор значень функції
n=length(x);
%обчислення елементів матриці
r=x.^2;
M(1,1)=1/n*sum(r);
M(1,2)=1/n*sum(x);
M(2,1)=M(1,2);
M(2,2)=1;
%обчислення елементів вектора d
d(1,1)=1/n*dot(x,y);
%dot-скалярний добуток векторів
d(2,1)=1/n*sum(y);
%розвязування системи лінійних рівнянь
coef=inv(M)*d;
Послідовність команд:
>> x=[1.01 1.04 1.11 1.16 1.2]
x =
1.0100 1.0400 1.1100 1.1600 1.2000
>> y=[4.4912 4.6584 5.0687 5.3799 5.6402]
y =
4.4912 4.6584 5.0687 5.3799 5.6402
>> coef=apr(x,y)
coef =
6.0362
-1.6162
>> Y=coef(1)*x+coef(2);
>> plot(x,y,x,Y)
Для побудови
квадратичного многочлена скористаємось
формулою
.
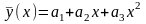Тоді
.
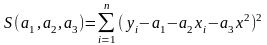Міркуючи
аналогічно, обчислимо
,
і
.
Розв’язання в середовищі MATLAB.
P(x)=a*x*x+b*x+c
Запишемо систему (2) для квадратичного многочлена:
(наступні перетворення аналогічні, як для лінійної функції)
function coef=apr2(x,y)
%апроксимація квадратичним многочленом y=a*x*x+b*x+c
%X -вектор значень аргумента
%У -вектор значень функції
n=length(x);
%
обчислення
елементів матриці
M(1,1)=1/n*sum(x.^4);
M(1,2)=1/n*sum(x.^3);
M(1,3)=1/n*sum(x.^2);
M(2,1)=M(1,2);
M(2,2)=M(1,3);
M(2,3)=1/n*sum(x);
M(3,1)=M(2,2);
M(3,2)=M(2,3);
M(3,3)=1;
%обчислення елементів вектора d
d(1,1)=1/n*dot(x.^2,y);%dot-скалярний добуток векторів
d(2,1)=1/n*dot(x,y);
d(3,1)=1/n*sum(y);
%розвязування системи лінійних рівнянь
coef=inv(M)*d;
Послідовність команд:
>> x=[1.01 1.04 1.11 1.16 1.2]
x =
1.0100 1.0400 1.1100 1.1600 1.2000
>> y=[4.4912 4.6584 5.0687 5.3799 5.6402]
y =
4.4912 4.6584 5.0687 5.3799 5.6402
>> coef=apr2(x,y)
coef =
-0.0007
0.2144
-0.0348
>> Y=coef(1)*x.^2+coef(2)*x+coef(3);
>> plot(x,y,x,Y)
Графіки функції, заданої у вигляді таблиці, і функції-апроксимуючого полінома співпадають.