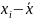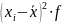- •Розділ 2. Кореляційне дослідження
- •2.1. Кореляційний аналіз залежності виробництва лляних тканин від валового збору льону-довгунця
- •Розділ 3. Практична частина курсової роботи Завдання 1
- •1. Групування атп за кількістю вантажних автомобілів.
- •2. Групування за коефіцієнтом використання вантажних автомобілів.
- •Завдання 2
- •1. Середня кількість вантажних автомобілів для всієї сукупності і для кожної групи окремо.
- •2. Мода і медіана за допомогою формул та графічно
- •Завдання 3
- •1.1. Середнє значення рівня ряду
- •1.2. Абсолютні прирости, коефіцієнти зростання, темпи приросту, темпи зростання, абсолютні значення одного проценту приросту:
- •1.3 Середні узагальнюючі показники ряду динаміки :
- •2. Аналіз сезонних коливань витрат на рекламу
- •Завдання 4
- •Індивідуальні індекси:
- •2. Середньорічна заробітна плата працівників по двох підприємствах, зміна її рівня окремо на кожному підприємству чи зміна в структурі чисельності працівників підприємств.
- •Список використаноїлітератури
Завдання 2
За результатами типологічного групування, що виконане в завданні 1, розрахувати:
1) середню кількість вантажних автомобілів для всієї сукупності і для кожної групи окремо;
2) моду і медіану за допомогою формул та графічно;
3) показники варіації кількості вантажних автомобілів: розмах варіації, середнє лінійне і квадратичне відхилення, загальну дисперсію трьома методами; коефіцієнт осциляції, квадратичний коефіцієнт варіації; групові дисперсії виробітку на 100 машинотон та середню з групових дисперсій, між групову і загальну дисперсії за цією ж ознакою та за правилом складання дисперсій перевірити рівність суми середньої з групових і між групової дисперсій загальній; коефіцієнт детермінації, емпіричне кореляційне відношення, дисперсію долі автотранспортних підприємств третьої групи.
Зробити висновки.
Розв’язок:
1. Середня кількість вантажних автомобілів для всієї сукупності і для кожної групи окремо.
Таблиця 3.2.1
Розрахункові дані для обчислення характеристики варіації
Групи АТП за кількістю автомобілів |
Кіль-кість авто |
Розрахункові величини |
||||
Середина інтервалу |
|
|
|
|
||
[23-37,25) |
5 |
30,13 |
150,65 |
-25,63 |
128,15 |
3284,485 |
[37,25-51,5) |
4 |
44,38 |
177,52 |
-11,38 |
45,4 |
518,018 |
[51,5-65,7) |
7 |
58,6 |
410,2 |
2,84 |
19,88 |
56,459 |
[65,7-80] |
9 |
72,85 |
655,65 |
17,09 |
153,81 |
2628,613 |
Разом |
25 |
- |
1394,02 |
- |
347,24 |
6487,575 |
Середня кількість вантажних автомобілів для всієї сукупності:

де - середина інтервалу,
 – кількість
АТП.
– кількість
АТП.
Середня кількість вантажних автомобілів для кожної групи окремо:
2. Мода і медіана за допомогою формул та графічно
Таблиця 3.2.2
Дані для обчислення характеристик центру розподілу
Групи АТП за кількістю вантажівок |
Кількість АТП |
Накопичена частота |
[23-37,25) |
5 |
5 |
[37,25-51,5) |
4 |
9 |
[51,5-65,7) |
7 |
16 |
[65,7-80] |
9 |
25 |
Всього |
25 |
- |
Мода:

де
 - нижня границя модального інтервалу,
- нижня границя модального інтервалу,
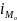 -
розмір модального інтервалу,
-
розмір модального інтервалу,
 -
частота модального інтервалу,
-
частота модального інтервалу,
 -
частота попереднього інтервалу,
-
частота попереднього інтервалу,
 -
частота інтервалу наступного за
модальним.
-
частота інтервалу наступного за
модальним.
Модальний інтервал : [65,7-80]
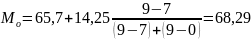

Рис. 3.2.1 Графічне зображення моди.
Медіана:
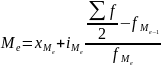
де
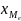 - нижня границя медіанного інтервалу,
- нижня границя медіанного інтервалу,
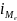 -
розмір медіанного інтервалу,
-
розмір медіанного інтервалу,
 -
пів сума накопичених частот,
-
пів сума накопичених частот,
 -
сума накопичених частот, які передують
медіанному інтервалу.
-
сума накопичених частот, які передують
медіанному інтервалу.
 – частота
медіанного інтервалу
– частота
медіанного інтервалу
Медіанний інтервал:


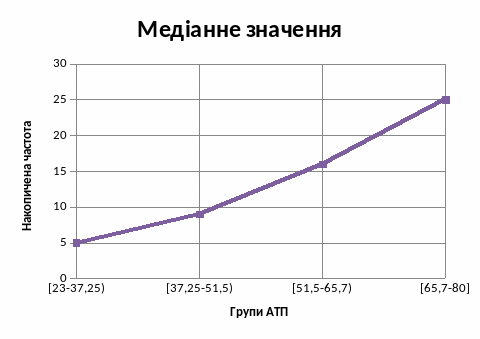
Рис. 3.2.2 Графічне зображення медіани
3.Показники варіації кількості вантажних автомобілів:
Розмах варіації:


Середнє лінійне відхилення:

Де - індивідуальне значення ознаки,
 -
середнє значення ознаки,
-
середнє значення ознаки,
- частота ознаки.
Середнє квадратичне відхилення:

Визначаємо дисперсію:
А) Як квадрат квадратичного відхилення:
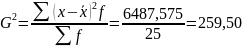
Б) Як різницю квадратів:

В) За методом моментів:

де

За A вибираємо число, яке знаходиться посередині варіаційного ряду:
ширина інтервалу.
i=14,25
A= (58,6+56,8)/2=57,7



Коефіцієнт осциляції:

де
 -
розмах варіації,
-
розмах варіації,
- середнє значення ознаки.

Квадратичний коефіцієнт варіації:

Оскільки
 ,
то статистична сукупність вважають
однорідною, а середню типовою.
,
то статистична сукупність вважають
однорідною, а середню типовою.
Групування АТП за виробітком на 100 машинотон:
Крок зміни (за виробітком на 100 машинотон):

[ 124 – 138,5) =124,129,132,138,132,132,132,132,138. (разом 9)
[138,5-153) =139,139,144,145,140,148,144,148,144. (разом 9)
[153 -167,5) = 162,167,159,158,. (разом 4)
[ 167,5- 182] = 182,182,182. (разом 3) Таблиця 3.2.3
Комбінаційний розподіл АТП за кількістю автомобілів та за
виробітком на сто машинотон.
АТП за кількістю автомобілів |
За виробітком на 100 машинотон, т/км |
Разом |
||||
[ 124 –138,5) |
[138,5 - 153) |
[153 -167,5) |
[ 167,5 - 182] |
|||
[23-37,25) |
4 |
- |
- |
1 |
5 |
|
[37,25-51,5) |
1 |
2 |
1 |
- |
4 |
|
[51,5-65,7) |
2 |
5 |
- |
- |
7 |
|
[65,7-80] |
2 |
2 |
3 |
2 |
9 |
|
Разом |
9 |
9 |
4 |
3 |
25 |
|
Розраховуємо середній виробіток на 100 машинотон для всієї сукупності:

Розрахуємо середній виробіток на 100 машинотон для кожної групи:

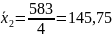


Таблиця 3.2.4
Розрахункові дані для обчислення групових дисперсій
Кількість вантажних автомобілів |
Виробіток на 100 машинотон |
Кіль-кість АТП |
Розрахункові дані |
|||
|
|
|
|
|||
[23-37,25) |
[ 124 -138,5) |
4 |
131,25 |
525 |
-8,95 |
320,41 |
[138,5-153) |
0 |
145,75 |
0 |
5,9 |
0 |
|
[153-167,5) |
0 |
160,25 |
0 |
20,3 |
0 |
|
[ 167,5-182] |
1 |
174,75 |
174,75 |
34,8 |
1211,04 |
|
Разом |
- |
5 |
- |
699,75 |
- |
1531,45 |
[37,25-51,5) |
[ 124 -138,5) |
1 |
131,25 |
131,25 |
-14,5 |
210,25 |
[138,5-153) |
2 |
145,75 |
291,5 |
0 |
0 |
|
[153-167,5) |
1 |
160,25 |
160,25 |
14,5 |
210,25 |
|
[ 167,5-182] |
0 |
174,75 |
0 |
29 |
0 |
|
Разом |
- |
4 |
- |
583 |
- |
420,5 |
[51,5-65,7) |
[ 124 -138,5) |
2 |
131,25 |
262,5 |
-10,36 |
214,66 |
[138,5-153) |
5 |
145,75 |
728,75 |
4,14 |
85,70 |
|
Продовження таблиці 3.2.4 |
||||||
[153-167,5) |
0 |
160,25 |
0 |
18,64 |
0 |
|
[ 167,5-182] |
0 |
174,75 |
0 |
33,14 |
0 |
|
Разом |
- |
7 |
- |
991,25 |
- |
300,36 |
[65,7-80] |
[ 124 -138,5) |
2 |
131,25 |
262,5 |
-22,56 |
1017,91 |
[138,5-153) |
2 |
145,75 |
291,5 |
-8,06 |
129,93 |
|
[153-167,5) |
3 |
160,25 |
480,75 |
6,44 |
124,42 |
|
[ 167,5-182] |
2 |
174,75 |
349,5 |
20,94 |
876,97 |
|
Разом |
- |
9 |
- |
1384,25 |
- |
2149,23 |
Всього |
- |
- |
- |
3658,25 |
|
4401,54 |
Обчислимо внутрішньо групові дисперсії:
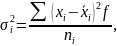
де
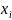 ,
,
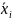 – значення окремих елементів сукупності,
– значення окремих елементів сукупності,
– кількість АТП.

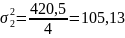
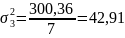

Середня з внутрішньо групових дисперсій:

Міжгрупова дисперсія:

де - групові середні
- загальна середня для всієї сукупності
 -
чисельність окремих груп
-
чисельність окремих груп

= 34,57
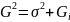

Перевіримо отриманий результат:
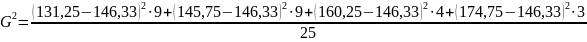
=209,91
Результати майже збіглися, відхилення виникло за рахунок заокруглень.
Обчислимо коефіцієнт детермінації:
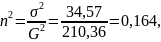
Це означає, що 16,4% загальної дисперсії виробітку на 100 машинотон обумовлене кількістю вантажних автомобілів, а решта зумовлене іншим фактором.
Емпіричне кореляційне відношення
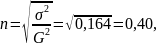
Тобто залежність між середнім виробітком на 100 машинотон і кількістю вантажних автомобілів становить 40% .
Розраховуємо дисперсію частин АТП третьої групи.
Частка підприємств третьої групи складає:

Тоді дисперсія:

Висновок:
Середня
кількість вантажних автомобілів для
всієї сукупності становить
 автомобілів. Центр ряду розподілу (моду)
і медіану обчислювали за допомогою
формул і графічно, результати за двома
показниками становлять відповідно
автомобілів. Центр ряду розподілу (моду)
і медіану обчислювали за допомогою
формул і графічно, результати за двома
показниками становлять відповідно
 та
та

Розраховуючи
показники варіації кількості вантажних
автомобілів отримали, що розмах варіації
склав 57, а відхилення варіюючої ознаки
від середньої величини 14 автомобілів.
Дисперсія обчислена трьома методами
становить
 ,
а середнє квадратичне відхилення
,
а середнє квадратичне відхилення
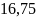 .
Статистична сукупність однорідна є
однорідною, про це свідчить коефіцієнт
варіації, який менше 33%. Загальна дисперсія
виробітку на 100 машинотонн склала
.
Статистична сукупність однорідна є
однорідною, про це свідчить коефіцієнт
варіації, який менше 33%. Загальна дисперсія
виробітку на 100 машинотонн склала
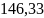 .
.
Коефіцієнт
детермінації становить
 ,
а це означає, що 16,4% загальної дисперсії
виробітку на 100 машинотонн обумовлено
кількістю вантажних автомобілів, а
решта 83,6% зумовлена іншими факторами.
,
а це означає, що 16,4% загальної дисперсії
виробітку на 100 машинотонн обумовлено
кількістю вантажних автомобілів, а
решта 83,6% зумовлена іншими факторами.
Емпіричне
кореляційне відношення дорівнює
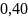 і показує, що залежність між виробітком
на 100 машинотонн і кількістю вантажних
автомобілів середня.
і показує, що залежність між виробітком
на 100 машинотонн і кількістю вантажних
автомобілів середня.