Лекция 1. Радиоактивность. Характеристики излучений

1. Здравствуйте.

2. Ионизирующее излучение (и.и.) — это любой вид излучения, взаимодействие которого со средой приводит к образованию ионов разных знаков. Различают непосредственно и.и. и косвенно и.и.

Непосредственно и.и. состоит из заряженных частиц, кинетическая энергия которых достаточна для ионизации при столкновении с атомом вещества. В качестве примера это могут быть протоны, электроны, альфа-частицы и т. д.

Косвенно и.и. — это поток незаряженных частиц, например, нейтронов, гамма-квантов, взаимодействие которых со средой приводит к появлению заряженных частиц, способных непосредственно вызвать ионизацию.

И.и., состоящее из частиц одного вида одинаковой энергии, называется моноэнергетическим однородным излучением.

И.и., состоящее из частиц одного вида различных энергий, называется немоноэнергетическим. Так, бета-излучение радиоактивных нуклидов всегда является немоноэнергетическим. Излучение, состоящее из частиц различного вида, называют смешанным.

3. В зависимости от характера распространения в пространстве различают направленное и ненаправленное и.и. Направленным называют излучение с выделенным направлением распространения. Если все направления распространения излучения равновероятны, говорят, что излучение изотропно.

4. Обычно различают первичное и вторичное и.и. Под первичным понимается и.и., которое в рассматриваемом процессе взаимодействия со средой принимается за исходное. Вторичное и.и. возникает в результате взаимодействия первичного и.и. с данной средой.

Распределение и.и. в рассматриваемой среде называется полем и.и. В зависимости от величины, характеризующей и.и., различают характеристики поля излучения. В дозиметрии под полем излучения понимают область пространства, каждой точке которой поставлены в соответствие физические величины, являющиеся характеристиками поля излучения.

5. Пусть параллельный пучок излучения направлен по нормали к поверхности поглощающей и рассеивающей сред. Число частиц F, переносимых излучением через единицу площади за некоторый промежуток времени называется флюенсом. Таким образом, для направленного излучения флюенс F — это число частиц, проходящих через перпендикулярно расположенную по отношению к направлению распространения излучения поверхности.

6. Рассмотрим теперь два пучка излучения, приходящих в некоторую точку A по двум различным направлениям от источников и (рис.1).

Рис.1. Излучение двух источников

Результирующий флюенс в точке A равен сумме флюенсов и излучений соответствующих источников.

Флюенс равен числу частиц, прошедших за время наблюдения через площадку единичной площади, расположенной перпендикулярно направлению . Чтобы найти флюенс , надо эту площадку повернуть около точки А так, чтобы она была перпендикулярна направлению и измерить прошедшее через нее число частиц за то же время. Результирующий флюенс .

7. Такое правило получения результирующего флюенса в некоторой точке пространства применимо для любого числа пучков излучений, приходящих в эту точку по различным направлениям.

Представим, что единичная площадка имеет форму круга. В общем случае, при различных ориентациях площадки относительно центра ее контур опишет сферу с радиусом, равным радиусу площадки. Суммарный флюенс частиц от всех источников оказывается равным числу частиц, проникающих в эту сферу.

8. Флюенс частиц — это отнесенное к площади поперечного сечения элементарной сферы число частиц излучения, проникающего в эту сферу. Под элементарной сферой понимают такую сферу, в пределах объема которой характеристики поля излучения можно считать неизменными. Иногда вместо термина флюенс используется термин перенос.

Если за интервал времени dt изменение флюенса частиц равно dF,то отношение представляет плотность потока частиц.

9. Плотность потока частиц — это отнесенное к площади поперечного сечения элементарной сферы число частиц излучения, проникающего в единицу времени в объем этой сферы. Для обозначения плотности потока частиц используется буква Ф или φ.

10. Рассмотрим моноэнергетическое излучение с энергией E. Если в некоторой точке пространства плотность потока равна Ф, то, умножив плотность потока частиц на энергию частиц E, получим плотность потока энергии или интенсивность излучения I:

(1.1)

.

Соотношение между флюенсом частиц F, плотностью потока частиц Ф и интенсивностью моноэнергетического излучения I можно представить в виде

(1.2)

,

где T промежуток времени.

11. Иногда используется понятие потока П ионизирующих частиц, который определяют как отношение числа частиц dN, проникающих через данную поверхность за промежуток времени dt к этому промежутку:

(1.3)

.

Очевидно, что связь плотности потока частиц с потоком определяется соотношением

(1.4)

.

12. Введенные в этом разделе характеристики поля излучения — положительные скалярные величины. В том виде, как эти величины даны здесь, они являются интегральными характеристиками поля и не дают представления об энергетическом и угловом распределениях излучения. Измеряют: плотность потока в см^-2·с^-1,(в ед. СИ м^-2·с^-1), поток в с^-1, интенсивность в МэВ·см^-2·с^-1, (СИ Дж·м^-2·с^-1). Более полную информацию о поле излучения дают дифференциальные характеристики, т. е. функции распределения. В частности, энергетическое распределение излучения φ(E) (или Ф(E)) позволяет получить ответ на вопрос сколько частиц, обладающих энергией E, пересекают единичную площадку за единичный интервал времени. Размерность Ф(E) — см^-2·с^-1·МэВ^-1 (в СИ м^-2·с^-1·Дж^-1). График зависимости Ф(E) от E часто называют энергетическим спектром излучения. На рис.2 в качестве примера приводятся спектры нейтронов за защитой ядерного реактора.

Рис.2. Спектры быстрых нейтронов за защитой реактора из серпентинитового бетона

13. Основной физической величиной, определяющей степень радиационного воздействия, является поглощенная доза и.и.

Поглощенная доза и.и. Д — отношение средней энергии , переданной и.и. веществу в элементарном объеме, к массе dm вещества в этом объеме

(1.6)

.

Единица поглощенной дозы в СИ — грей (Гр). Грей равен поглощенной дозе и.и. при которой веществу массой 1 кг передается энергия и.и. 1 Дж.

Продолжение про дозовые характеристики

1. Под переданной энергией в определении поглощенной дозы понимается

(1.7)

,

где  — суммарная кинетическая энергия всех непосредственно и косвенно ионизирующих частиц, которые входят в рассматриваемый объем,  — соответственно, кинетическая энергия частиц, которые покидают указанный объем. Внутри данного объема возможны ядерные реакции и превращения элементарных частиц. В этих случаях возможны как выделение, так и затраты энергии. Суммарная выделившаяся при этом энергия в (1.7) обозначена , а суммарная затраченная энергия — соответственно .

2. Переданная энергия реализуется (расходуется) в процессах ионизации, возбуждения ядер или атомов, упругих столкновениях. Статистический характер взаимодействий излучений с веществом приводит к тому, что переданная некоторому объему вещества энергия излучения оказывается случайной (стохастической) величиной. По этой причине в определении поглощенной дозы и входит средняя энергия , которая, в свою очередь, является нестохастической величиной. Следовательно, и поглощенная доза — величина нестохастическая.

3. Строго говоря, следует различать переданную энергию и поглощенную энергию излучения в указанном объеме. Как правило, это существенно на границах раздела различных сред, где нет «электронного равновесия». В задачах, которые будут рассмотрены в настоящем курсе, этим различием мы пренебрегаем.

4. Доза излучения зависит от времени облучения; с течением времени доза накапливается. Изменение дозы в единицу времени называется мощностью дозы. Мощность дозы равна

(1.8)

.

В общем случае мощность дозы является функцией времени — P(t). Если эта функция известна, то дозу за некоторый интервал времени от до можно определить по формуле

(1.9)

.

Если мощность дозы постоянна во времени, то

(1.10)

Д=P(t₂-t₁).

5. Экспозиционная доза — это дозовая характеристика фотонного излучения. Она равна абсолютному значению полного заряда ионов одного знака, которые образуются в воздухе при полном торможении электронов и позитронов, освобождаемых фотонами в единице массы воздуха. Обозначим экспозиционную дозу X, тогда

(1.11)

,

где dQ — суммарный заряд всех ионов одного знака, созданных в воздухе при полном торможении электронов и позитронов, освобождаемых фотонным излучением в массе воздуха dm. Отметим, что заряд dQ включает заряд всех ионов одного знака, созданных в результате полного использования кинетической энергии электронов и позитронов в воздухе независимо от места образования этих ионов; важно лишь, что эти ионы созданы электронами и позитронами, которые возникли в массе воздуха dm.

6. Понятие экспозиционной дозы рекомендовано для фотонного излучения с энергией до 3 МэВ. Единица экспозиционной дозы в СИ — кулон на килограмм (Кл/кг).

Кулон на килограмм равен экспозиционной дозе, при которой все электроны и позитроны, освобожденные фотонами в объеме воздуха массой 1 кг, производят в воздухе ионы, несущие электрический заряд каждого знака 1 Кл.

7. Воздух, выбранный в качестве модельной среды в определении экспозиционной дозы, имеет эффективный атомный номер близкий к эффективному атомному номеру ткани для фотонного излучения с энергией до 3 МэВ, иначе говоря, воздух можно считать тканеэквивалентной средой.

8. Из определения единиц экспозиционной дозы нетрудно найти их энергетические эквиваленты. Известно, что средняя энергия ионизации e (энергия образования одной пары ионов) в воздухе равна 33 эВ. Ее определяют как отношение начальной кинетической энергии E заряженной ионизирующей частицы к числу пар ионов n, образованных этой частицей до полной потери ее энергии в данном веществе: . Принимая заряд одного иона равным 1,602·10^-19 Кл, получаем энергетические эквиваленты кулона на килограмм:

1 Кл/кг = 6,24·10¹⁸ пар ионов на 1 кг воздуха,

1 Кл/кг = 6,24·10¹⁸·e = 2,11·10¹⁴ МэВ на 1 кг воздуха,

1 Кл/кг = 33,85 Дж/кг.

9.Впрочем, экспозиционная доза в настоящее время более или менее современными справочниками и НД (В частности, НРБ) к использованию не рекомендуется. Но упомянуть о ней необходимо как минимум для удобства чтения старой литературы. Так, например, все сведения о былых радиационных авариях. в частности ЧАЭС, оперируют дозами в рентгенах и фоном в мкР/ч (или Р/час) Внесистемная единица экспозиционной дозы — рентген (Р). Рентген — это единица экспозиционной дозы фотонного излучения, при прохождении которого через 0,001293 г воздуха в результате завершения всех ионизационных процессов в воздухе создаются ионы, несущие одну электростатическую единицу количества электричества каждого знака. 0,001293 г — это масса 1 см³ атмосферного сухого воздуха при нормальных условиях (температура 0°С и давления 1013 гПа (760 мм рт. ст.)). Соотношение между рентгеном и единицей системы Си: 1Р = 2,58·10^-4 Кл/кг.

10. Результат воздействия излучения на объект определяется не только поглощенной энергией, но и характером распределения этой энергии в облучаемом объекте, видом излучения, распределением облучения во времени и др. факторами. Оказывается, что даже частицы одной природы, но разных энергий могут вызвать неодинаковый радиационный эффект при одной и той же поглощенной дозе.

Считается, что ионизация живой ткани играет определяющую роль в биологическом действии и.и. Свойства ионов не зависят от того, как они возникли, а, следовательно, и от природы ионизирующих частиц. Однако разные виды излучений создают ионы с неодинаковым пространственным распределением. Например, тяжелые заряженные частицы создают более плотный трек ионов, чем легкие; различными оказываются диапазоны энергий, передаваемых δ-частицам (освобожденным электронам).

Под качеством понимают такую характеристику излучения, которая имеет одно и тоже значение у разных видов излучения, если при одинаковых условиях облучения данного объекта и одинаковой дозе наблюдается один и тот же радиационный эффект. Иначе говоря, радиационной действие излучений одинакового качества будет одинаковым при равных дозах.

Коэффициент качества (кк) является регламентированной величиной, устанавливаемой специальными научными комиссиями на основании медицинских и радиобиологических данных. Помимо численных значений коэффициент качества для различных видов излучений устанавливается зависимость кк от ЛПЭ излучения. Излучение с одинаковым кк при равных дозах и одинаковых условиях облучения приводит к одинаковому биологическому эффекту. Итак, коэффициент качества есть зависящий от ЛПЭ коэффициент, на который надо умножить поглощенную дозу, чтобы для целой радиационной защиты биологический эффект облучения людей выражался в одной и той же мере независимо от вида излучения.

В практической дозиметрии используют следующие значения коэффициентов качества различных видов излучения с неизвестным спектром.

Таблица 1.1

Рекомендуемые значения кк для излучения с неизвестным энергетическим составом, Зв/Гр

Вид излучения	кк
Рентгеновское и гамма-излучение, -излучение позитроны	1
Нейтроны с энергией меньше 20 кэВ	3
Нейтроны с энергией 0,1 МэВ – 10 МэВ	10
Протоны с энергий меньше 10 МэВ	10
Альфа-излучение с энергией меньше 10 МэВ	20
Тяжелые ядра отдачи	20

Эквивалентная доза и.и. H — это произведение поглощенной дозы Д на коэффициент качества

.

Единица эквивалентной дозы СИ — зиверт (Зв). Зиверт равен эквивалентной дозе, при которой произведение поглощенной дозы в биологической ткани стандартного состава на кк равно 1 Дж/кг. Иначе говоря, зиверт — единица эквивалентной дозы любого вида излучения в биологической ткани, которое создает такой же биологический эффект, как и поглощенная доза в 1 Гр образцового (кк = 1) рентгеновского или гамма-излучения.

Для смешанного излучения эквивалентная доза определяется как произведение поглощенных доз отдельных видов излучений D_i на соответствующие значения :

где i, индекс вида и энергии излучения.

Биологическая ткань стандартного состава, рекомендованная ГОСТ, содержит кислород – 76 %, водорода – 10,1 %, углерода – 11,1 %, азота – 2,6 % по массовому составу.

Следует заметить, что поглощение излучения (энергии) живой тканью – процесс сугубо неравномерный, как по глубине, так и по части «вредности» для различных видов поглощающих тканей.

(здесь про весовые коэффициенты органов)

Не все органы одинаково воспринимают облучение.

Вот таблица

Лекция 2. Керма-постоянные и керма-эквиваленты. Взаимодействие ИИ с веществом (гамма)

1. Еще одна дозовая характеристика незаряженного излучения – керма (от английского «kinetiс energy released in material») отношение суммы первоначальных кинетических энергий dE_K всех заряженных частиц, образовавшихся под действием косвенно ионизирующего излучения в элементарном объеме вещества, к массе в этом объеме:

K = dE_K/dm

Керма применима, как для фотонов, так и для нейтронов в любом диапазоне доз и энергий излучения. Керму измеряют в тех же единицах, что и поглощенную дозу. Соответственно мощность кермы есть отношение приращения кермы dK за интервал времени dt к этому интервалу времени:

= dK/dt.

Разница кермы и поглощенной дозы в том, что керма в общем случае больше, т.к. тормозное вторичное излучение может вынести часть энергии, входившей в керму, вовне рассматриваемого объема. Керма используется в настоящее время как распространенная замена выведенной из нормативной документации экспозиционной дозе.

2. Биологический эффект для разных видов ионизирующих излучений не одинаков при прочих равных условиях, в том числе, при одинаковой поглощенной дозе. Оказывается важно не только количество ионов, образованных в единице массы биологической ткани, но и то, как распределены эти ионы по длине пути, т.е. осуществлена линейная плотность ионизации. Ее однозначно характеризует линейная передача энергии (ЛПЭ) излучения, L — отношение полной энергии dE, переданной веществу заряженной частицей вследствие столкновений на элементарном пути dl, к длине этого пути:

L =dE/dl

В качестве единицы измерения ЛПЭ используется килоэлектронвольт на микрометр воды, 1 кэВ/мкм: 1 кэВ/мкм = 0,16 нДж/м.

Керма-постоянная и κερμα-эквивалент источника

3. При работе с радионуклидами необходимо помнить, что число распадов источника γ-излучения не определяет степень его ионизирующего воздействия. Оно также зависит от схемы распада, т.е. количества фотонов, приходящихся на один распад, и энергии фотонов. Поэтому вводят величины однозначно характеризующие данный радионуклид как γ-излучатель. Такими характеристиками являются гамма-постоянная и гамма-эквивалент радионуклида. Как известно, гамма-эквивалент и гамма-постоянная определяются через экспозиционную дозу. В связи с переходом к СИ и отказом от использования экспозиционной дозы, как дозиметрической величины, введены новые величины для характеристики источников γ-излучения: керма-постоянная и керма-эквивалент соответственно. Керма- постоянная (постоянная мощности воздушной кермы радионуклида) Г_δ определяется как отношение мощности воздушной кермы К, создаваемой фотонами с энергией больше заданного порогового значения от точечного изотропно-излучающего источника данного радионуклида, находящегося в вакууме* на расстоянии l οт источника, умноженной на квадрат этого расстояния к активности А источника:

Г_δ = (К×l²)/A.

* Подчеркнуто, что источник находится в вакууме. Это означает, что в пространстве, окружающем элементарный воздушный объем в точке детектирования, рассеяния и поглощения не происходит.

Единица керма-постоянной в СИ — [Гр·м²/(с·Бк)].

И, естественно, зная керма-постоянные, активности радионуклидов и расстояния от источника до детектора легко из формулы (3.25) определить мощность воздушной кермы:

K = A·Г_δ/l².

4. Различают керма-постоянную дифференциальную – только от отдельных энергий гамма-квантов и общую (интегральную) – суммарную ото всех.

5. Керма-эквивалент источника K₁ — мощность воздушной кермы К γ-излучения с энергией фотонов больше заданного порогового значения d точечного изотропно-излучающего источника, находящегося в вакууме на расстоянии l от источника, умноженная на квадрат этого расстояния:

K₁=K·l²

Керма-эквивалент объемного источника равен сумме керма-эквивалентов составляющих его точечных источников с учетом самопоглощения, возможного ослабления излучения в окружающей источник среде и рассеяния в источнике и окружающей среде

6. Некоторые данные для распространенных нуклидов

Таблица 3.7. Керма-постоянная Γ_δ; гамма-постоянная Γ_γ; керма-эквивалент K_i и гамма-эквивалент m для некоторых радионуклидов

Нуклид	Период полурас-пада T	Гδ, аГр·м2 (с-Бк)	Гγ Р·см2/ (ч·мКи)	K1 нГр·м·с	m мг·экв Ra
40K	1,28×109л.	5,1	0,19	1,9	0,09
60Со	5,3 года	84,6	13,0	3,1	1,54
131J	8,0 сут.	14,2	2,2	0,52	0,26
137Cs	30 лет	21,3	3,2	0,80	0,40
134Cs	2,0 года	57,4	8.7	2,06	1,03
155Eu	5,0 лет	2.6	0,4	0,1	0,05
170Tm	129 сут	0,2	0,008	0,06	0,004
192Ir	74 сут.	30,0	4,6	1,1	0,54
226Ra*	1600 лет	59,5	9,0	2,14	1,07
226Ra**	1600 лет	55,3	8,4	2.0	1

7. Законы взаимодействия ионизирующего излучения с веществом являются теоретической и практической основой радиационной защиты, на них базируются методы расчета защиты и методы регистрации ионизирующего излучения.

Ионизирующее излучение, в зависимости от массы и заряда, можно подразделить на четыре группы:

•Тяжелые заряженные частицы, к ним относятся α-частицы, протоны и др.

• Легкие заряженные частицы: электроны и позитроны.

• Фотонное излучение: рентгеновское и γ-излучение.

• Нейтронное излучение: нейтроны различных энергий.

8. Можно провести связь между линейными потерями энергии и поглощенной дозой. Энергия излучения передается веществу в отдельных актах взаимодействия. Поэтому, чтобы определить поглощенную дозу, необходимо знать, как излучение взаимодействует с веществом. Поглощенная доза наиболее просто определяется в случае непосредственно и.и. Учитывая только ионизационные потери энергии (пренебрегая ядерными взаимодействиями) мощность дозы заряженных моноэнергетических частиц, ЛПЭ которых равно L, определяется формулой

,

где Ф — плотность потока частиц, а выражено в массовых единицах ( ), ρ — плотность вещества.

Применение массовых единиц рационально в связи с тем, что для взаимодействия среды и заряженных частиц определяющими являются кулоновские силы, величина которых на единицу пробега пропорциональна числу «встреченных» атомов, т.е. плотности вещества.

Для немоноэнергетического излучения со спектром Ф(Е), мощность дозы равна

,

9. С незаряженными частицами все сложнее. Принимая во внимание, что источниками и.и. при обсуждении вопросов радиационной защиты служит ядерный реактор, ограничимся энергиями гамма-квантов в интервале 50 кэВ – 10 МэВ и соответственно нейтронов 0,025 эВ – 14 МэВ.

10. Рассматриваются три основных механизма потери энергии: ионизация, возбуждение и торможение.

Ионизация атомов представляет собой процесс превращения нейтральных атомов среды под действием ионизирующего излучения в заряженные частицы — электроны и ионы, т.е. образование пары ионов. В этом процессе из нейтрального атома выбиваются электроны и он становится ионом. Комбинация выбитого электрона и ионизированного атома называется ионной парой. В различных материалах на образование ионной пары необходима энергия 30 — 40 эВ. Эта энергия называется энергией образования пары ионов ε. Для образования одной пары ионов в воздухе γ-излучение в среднем расходует энергию ε = 33,85 эВ на пару.

Для количественной оценки ионизации атомов вводят понятия полной ионизации и линейной плотности ионизации.

Полная ионизация N_n — это количество пар ионов, образованных ионизирующим излучением, на всем пути в среде:

N_n = Ε/ε,

где E — энергия ионизирующего излучения, эВ

11. Линейная плотность ионизации N_L (удельная ионизация) — это количество пар ионов, образованных ионизирующим излучением на единице пути:

N_L = N/R = E/sR, (2.2)

где N_n — полная ионизация пар ионов; R — линейный пробег.

10. Возбуждение атомов — это механизм потери энергии, являющийся следствием кулоновского взаимодействия между заряженной частицей и электронами атома. Если при ионизации удаление электронов с орбиты происходит путем их выбивания из нейтрального атома, то при возбуждении электрону передается энергия, недостаточная для его выбивания, в результате чего электрон переходит на более высокий энергетический уровень, при этом он удерживается атомом и нейтральность атома не нарушается. Этот процесс не ведет к образованию ионных пар и к появлению свободных зарядов в веществе. При переходе электрона на прежнюю орбиту испускается характеристическое излучение, энергия которого зависит от глубины перехода орбитального электрона. На каждую образованную пару ионов при ионизации атома приходится примерно два-три возбужденных атома. Потери энергии при ионизации и возбуждении атомов называются ионизационными потерями.

11. Торможение частиц в поле ядра. Потери энергии ионизирующего излучения в поле ядра называют радиационными потерями, они представляют из себя уменьшение энергии в результате торможения заряженной частицы в поле ядра поглотителя и связаны с испусканием тормозного излучения. Заряженные частицы, пролетая вблизи ядра атомов поглотителя, тормозятся в поле ядра и меняют направление своего движения. Причина возникновения тормозного излучения—это та же кулоновская сила, которая отклоняет заряженную частицу, изменяя направление ее движения. В физическом смысле изменение направления является замедлением т.к. меняется направление вектора скорости и уменьшается величина скорости из-за потери энергии. Тормозное излучение является фотонным излучением с непрерывным спектром, энергетический диапазон которого входит в диапазон рентгеновских лучей. Тормозное излучение возникает в рентгеновских трубках, в ускорителях электронов и др. Анализ процесса потери энергии на тормозное излучение показывает, что эти потери прямо пропорциональны энергии заряженной частицы и квадрату атомного номера поглотителя, и обратно пропорциональны квадрату массы заряженной частицы. Например, потери энергии протона примерно в 2000² раз меньше потерь энергии электрона.

В случае, когда поглощающим веществом является человеческое тело, на ионизацию и возбуждение приходится 99% поглощенной энергии, в то время, как на тормозное излучение 1% энергии.

12. Основными процессами взаимодействия гамма-квантов в указанном интервале энергий являются: фотоэффект, комптоновское рассеяние и эффект образования электронно-позитронных пар.

Фотоэффект. При фотоэффекте гамма-квант поглощается атомом и освобождается электрон. Если энергия связи электрона в атоме равна , а энергия гамма-кванта , то справедлива следующая формула

(2.4)

,

где  — кинетическая энергия вылетевшего электрона. Вылетевший из атома электрон освобождает место на соответствующем энергетическом уровне, которое может быть занято менее связанным электроном. При переходе менее связанных электронов на вакантные уровни избыток энергии уносит характеристический гамма-квант.

Итак, при фотоэффекте часть энергии первичных фотонов (гамма-квантов) преобразуется в кинетическую энергию электронов (фотоэлектронов), а часть — в энергию характеристического излучения. Обозначив коэффициент фотоэлектрического преобразования τ, можем написать

(2.5)

,

где  — часть коэффициента фотоэлектрического поглощения, характеризующая преобразование энергии первичных фотонов в кинетическую энергию электронов;  — часть коэффициента фотоэлектрического поглощения, характеризующая преобразование энергии первичных фотонов в энергию характеристического излучения. Отметим, что в большинстве практических случаев роль коэффициента мала, т. е. вся энергия гамма-квантов преобразуется в энергию фотоэлектрона.

Фотоэффект играет важную роль при небольших энергиях гамма-квантов, (при энергиях < 0,5 МэВ τ убывает с ростом энергии по закону ). С увеличением атомного номера вещества Z, вероятность фотоэффекта возрастает по закону

(2.6)

,

где эмпирические коэффициенты m и n изменяются соответственно в диапазонах 4   4,6 и 3   1 в зависимости от энергии гамма-квантов.

Комптон-эффект — это рассеяние фотона на связанном в атоме (орбитальном) электроне. Обычно он происходит с большой вероятностью на внешних (наименее связанных) электронах атома. В отличие от фотоэффекта этот процесс не ведет к полному поглощению гамма-кванта: гамма-квант передает электрону часть энергии и изменяет направление своего движения. Обозначив линейный коэффициент комптоновского взаимодействия σ, получим

(2.7)

,

где и  — части коэффициента комптоновского взаимодействия, характеризующие преобразование энергии первичного фотона в энергию электронов отдачи и энергию рассеянных квантов соответственно. Так как при комптоновском рассеянии каждый электрон индивидуально участвует в процессе, то σ пропорционально Z. В зависимости от энергии гамма-кванта σ изменяется обратно пропорционально Е.

В пределах интересующего нас интервала энергий процесс комптоновского рассеяния является основным механизмом взаимодействия гамма-квантов с веществом.

Эффект образования пар — это процесс, когда в поле атома вместо фотона образуется электрон-позитронная пара. Для такого взаимодействия необходимо, чтобы энергия первичного фотона была больше 1,02 МэВ (удвоенной массы покоя электрона).

Закон сохранения энергии при этом записывается в виде

(2.8)

,

где и соответственно кинетические энергии электрона и позитрона.

Позитрон, замедлившись, взаимодействует с одним из электронов среды. В результате образуется два фотона аннигиляционного излучения с суммарной энергией 1,02 МэВ. Итак, при эффекте образования пар энергия первичных фотонов преобразуется в кинетическую энергию и.и. (электронов и позитронов) и в энергию аннигиляционного излучения.

Из рассмотренных трех процессов следует, что в первичных актах взаимодействия гамма-излучения с веществом часть энергии преобразуется в кинетическую энергию электронов и позитронов, а часть в энергию вторичного гамма-излучения.

Для моноэнергетического излучения одновременно можно наблюдать не более чем два процесса взаимодействия: либо фотоэффект и комптоновское рассеяние, либо Комптон-эффект и образование пар. Это вызвано тем, что для легких элементов, ( ), фотоэффект с увеличением энергии фотонов становится маловероятным раньше, чем появляется эффект образования пар. Если излучение немоноэнергетическое, все три эффекта могут наблюдаться одновременно.

Если μ — полный линейный коэффициент ослабления моноэнергетического излучения, тогда

(2.9)

μ = τ + σ + æ.

Линейный коэффициент ослабления μ по физическому смыслу — это макроскопическое сечение, обычно обозначаемое Σ в случае нейтронного излучения. Размерность линейного коэффициента ослабления см^-1.

Коэффициент μ входит в выражение закона ослабления (4.8),(4.9) функционалов поля и.и., в частности

(2.10)

,

где Ф(0) — плотность потока частиц, летящих перпендикулярно к поверхности плоского слоя вещества толщиной х, Ф(х) — плотность потока частиц не испытавших взаимодействия после прохождения слоя вещества толщиной х.

Формула (2.10) представляет собой закон ослабления нерассеянного излучения. Этот закон называют законом ослабления излучения в геометрии узкого пучка или в «хорошей» геометрии.

Коэффициент ослабления, рассчитанный на единицу массы ослабляющей среды, — массовый коэффициент ослабления — обозначим

(2.11)

.

Аналогичные (2.11) соотношения можно ввести для парциальных составляющих μ коэффициентов τ, σ, æ. Полный коэффициент ослабления μ сложным образом зависит от энергии гамма-квантов и материала поглотителя. Если вещество является химическим соединением различных атомов или их смесью, то его массовый коэффициент , см²/гр, определяется суммированием массовых коэффициентов отдельных составляющих с учетом их массового содержания :

(2.12)

.

Лекция 3. Взаимодействие ИИ с веществом (продолжение)

1. Энергия электронов , освобождаемых в единицу времени гамма-квантами в объеме V может быть записана через коэффициент передачи энергии

Линейный коэффициент передачи энергии µt_r – отношение доли энергии dε/ε косвено ионизирующего излучения, которая преобразуется в кинетическую энергию заряженых частиц при прохождении элементарного пути dl в веществе, к длине этого пути:

µ_tr = (dε/ε)/dl (1/см)

если ρ – плотность в г/см³, то

µ_tr.m = µ_tr/ρ (г/см²)

в виде

(2.16)

,

где Ф — плотность потока гамма-квантов,  — их энергия. Предполагается, что объем V достаточно мал, т. е. в его границах можно считать .

Разделив обе части (2.16) на массу вещества заключенного в объеме , получим выражение

(2.17)

,

где I — интенсивность гамма-излучения,  — энергия, переданная гамма-излучением электронам, отнесенная к единице массы вещества в единицу времени. Мы уже знаем, что эта величина называется керма.

2. Известно, что при достаточно больших энергиях электронов (выше 3 – 5 МэВ) они теряют энергию, испуская гамма-кванты тормозного излучения. Чтобы учесть тормозное излучение при нахождении мощности поглощенной дозы Р, приходиться вводить массовый коэффициент поглощения энергии гамма-квантов . Иногда его называют истинным массовым коэффициентом поглощения гамма-излучения, и обозначают . Тогда мощность поглощенной дозы Р следует представить, как

(2.18)

.

3. При энергии гамма-квантов ниже 3 МэВ (гамма-излучение всех радиоактивных изотопов) тормозным излучением электронов можно пренебречь и с точность не ниже 1 % можно считать , что равносильно соотношению . В общем случае мощность поглощенной дозы Р и мощность кермы совпадают только в условиях электронного (лучевого) равновесия, когда суммарная кинетическая энергия электронов и позитронов , освобожденных гамма-квантами в объеме V равна поглощенной в этом объеме энергии.

4. В случае немоноэнергетического излучения следует пользоваться следующими формулами при нахождении мощности кермы и поглощенной дозы

(2.19)

,

(2.20)

,

где и  — массовые коэффициенты передачи и поглощения, соответственно, для фотонов энергии . Как правило, в практике приводятся справочные значения как для энергий, так и для коэффициентов передачи / поглощения энергии в табличном виде.

5. Для практического расчета дозовых величин от конкретных источников нам нужно знать, какие нуклиды испускают какие частицы, в каком количестве и какой энергии. Для этого рассмотрим схемы распада.

Принятое обозначение схем распада

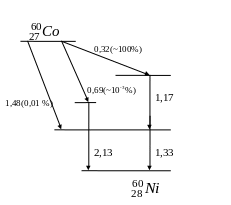
6. В качестве примера, на рис.2 показана схема распада радиоизотопа . У нуклида (рис.7), например, -частицы испускаются в 100 % случаев распада, соответственно в 100 % случаев распадов испускаются фотоны с энергиями 1,17 и 1,33 МэВ. Следовательно, этот радионуклид активностью, например 1 ГБк испускает фотонов с энергией 1,17 МэВ, фотонов с энергией 1,33 МэВ, фотонов с энергией 2,13 МэВ и -частиц в 1с.

7. Пусть имеется точечный (его размерами можно пренебречь) изотропный радионуклид активностью Q. В нем происходит Q распадов в 1с, а энергетический спектр гамма-излучения источника (он создается схемой распада, см. выше), содержит N групп фотонов; i-й группы (i=1,2,…N) энергия фотонов равна , МэВ, с фотонным выходом (число фотонов с энергией на один распад ядра) , фотон/расп.

Рассчитаем для этого источника характеристики поля излучения в воздухе в точке детектирования на расстоянии r, м, от источника. Воздух выбран в качестве стандартной среды, т. к. обычно в экспериментах по ионизационному эффекту в воздухе (естественных условиях) сравнивают фотонное излучение различных источников. Из-за малой плотности воздуха ( ) поглощением и рассеянием излучения в воздушной среде пренебрегаем, что эквивалентно рассмотрению задачи в вакууме.

Интенсивность (плотность энергии) фотонов I, в точке детектирования

(3.6)

.

Используя соотношение (2.20), заменяя интегрирование суммированием, имеем

(3.7)

где Q — активность источника, Бк;  — массовый коэффициент поглощения энергии фотонов в среде (например, в воздухе); W — энергетический эквивалент дозиметрической величины;  — коэффициент перевода 1 МэВ в джоули.

Если используется внемассовые единицы, то

(3.8)

,

где Q — активность источника в mKu,  — коэффициент перевода 1 МэВ в эрги.

В левых частях формул (3.7), (3.8) мощности дозы P, в зависимости от коэффициента W, может быть:

1. Поглощенная мощность дозы ,

2. Мощность кермы ,

3. Мощность экспозиционной дозы ,

4. Мощность эквивалентной дозы .

В таблице 3.1 указаны значения коэффициентов W, которые при подстановке в формулы (3.7) и (3.8) дают выражение для искомой величины P.

Таблица 3.1

Единицы величин , W и P в формулах (3.7) и (3.8)

Дозиметрическая величина	Система единиц		W	P
мощность поглощенной дозы	СИ	для воздуха	1
	внесис-темная	для воздуха	100
мощность кермы	СИ	для воздуха	1
	внесис-темная	для воздуха	100
мощность экспозиционной дозы	СИ	для воздуха	33,85
	внесис-темная	для воздуха	87,3
мощность эквивалентной дозы	СИ	для ткани	1
	внесис-темная	для ткани	100

В выражениях (3.9) и (3.10)  — массовый коэффициент поглощения энергии гамма-излучения в воздухе для энергии фотонов i-й . Для моноэнергетического излучения из формул (3.7) и (3.8), используя данные табл. 3.1 легко получить соотношение между мощностями эквивалентной и поглощенной доз

(3.11)

.

В диапазоне энергий 0.04 – 15 МэВ отношение . Следовательно, можно записать, что мощности эквивалентной дозы и поглощенной дозы в воздухе связаны соотношением

(3.12)

.

Если учесть, что для радионуклидных источников выражение (3.12) можно продолжить

(3.13)

,

где  —  переходный коэффициент от мощности кермы в воздухе к мощности эквивалентной дозы.

Таким образом, мы получили возможность, зная активность нуклида, рассчитать керма-постоянные для точечных источников, определить в зависимости от активности и расстояния мощности кермы, сами значения кермы, и перевести это в эквивалентную дозу от гамма-излучения. Для практических расчетов потребуются только знания схем распадов нуклидов и коэффициенты поглощения/передачи энергии в среде для заданных энергий.