Введение

Все задачи системного проектирования (построение моделей, параметрический анализ и синтез) являются оптимизационными. Анализ проектно-конструкторских решений (ПКР) с использованием имитационного моделирования стендовой отработки и натурных испытаний направлен на оценку показателей функционирования (ПФ) или их зависимости от контролируемых параметров для альтернативных вариантов технического комплекса (ТК).

Значение ПФ определяется усреднением по историям жизни ТК с учетом вероятности их появления и может быть представлено аналитически, если допустимы определенные упрощающие гипотезы о характере историй жизни и влиянии их на ПФ.

При неизменяющихся свойствах объекта и среды можно использовать классические методы математической статистики (интерполяционный метод, метод эквивалентных возмущений, метод Монте-Карло ) в зависимости от исходных данных о характеристиках воздействий и о виде функциональной зависимости ПФ от них. Однако в процессе проектирования и отработки эти условия нарушаются; предложенные Пупковым и Железновым способы оценки ПФ позволяют лишь частично учесть эти изменения.

Планирование разнотипных испытаний

Постановка и формальное решение задачи об оценке вероятности Р сложного события по частотам вероятности p_s элементарных событий:

, где

Формальное решение и использует искомые величины и не обеспечивает целочисленности n_s^opt, поэтому был предложен и обоснован итерационный подход, когда на начальном этапе часть (треть) ресурсов Ф, директивно распределена между разнотипными испытаниями в соответствии с гипотезой о близости p_sпо схеме с оценкой p_s по частоте элементарных событий или на основе биномиального закона для редких событий, а на последующих этапах проводятся дополнительныеl испытаний того типа, для которого , где - текущая оценка параметра y_s². Расчеты, показали сходимость и эффективность метода при оценке бортовых РЭК конкретного класса.

Для ТК кратковременного действия с надежными элементами и небольшой функциональной избыточностью можно при планировании разнотипных испытаний учитывать влияние только отдельных отказов (с вероятностью ): , где , - условные вероятности в определенных состояниях, - вероятность безотказной работы всех элементов, - вероятность отказа только одного их элементов

Тогда дисперсия относительной погрешности в оценке Р: , где , , а суммарные затраты

Формальное решение задачи ( ) дается формулами: , при и из (1) .

Т.к. , можно принять , где .

При директивном распределении ресурсов, полагая , получим и , где .С учетом этого имеем и .

Если ввести обозначения , то числитель равен .

С учетом величин второго порядка относительно z_s числитель равен и (т.к. ) окончательно имеем , где .

Принцип равного вклада для приближенного равенства , где - величина, обратно пропорциональная суммарной дисперсии ошибок элементов дает и .

Обработка результатов испытаний тк, при экспоненциальном изменении его свойств

В процессе испытаний ТК выявляются дефекты и вносятся изменения, направленные на их устранение. Результаты таких испытаний позволяли обосновать гипотезу об экспоненциальном характере роста вероятности успешной работы , где , i – номер испытания.

Пусть величина характеризует исход i-го испытания по оценке p_i: ξ=1 при удачном испытании, ξ=0 при неудачном испытании. Тогда количество успешных исходов после j испытаний ;

Соответствующий график – ступенчатую функцию (называемую траекторией успешных значений) можно аппроксимировать средним значением . После суммирования получаем при , , .

Развивая подход, предложенный Пупковым, потребуем .

Условия минимизации: дают систему линейных алгебраических уравнении относительно (b, -c, -1): 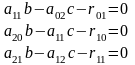, где , .

Определитель однородной системы должен быть равен нулю:

Теоретические и экспериментальные исследования, выполненные под руководством автора, показали, что внутри промежутка корень уравнения всегда существует и его можно найти одним из известных методов. По найденному определяем коэффициенты и , а затем , при

Экспертные оценки определены на основе результатов натурных испытаний системы самонаведения противокорабельных ракет определенного типа.

Таким образом, используя гипотезу об экспоненциальном росте вероятности успешной работы системы, можно аппроксимировать траекторию успешных испытаний и по результатам спрогнозировать её значения в ходе текущих испытаний; рассмотренный подход был распространен на определение текущих оценок математического ожидания и дисперсии погрешности функционирования.