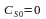Реакторы Периодического действия

Рисунок 177 - Реакторы периодического действия.

В реакторе периодического действия все отдельные стадии процесса протекают последовательно, в разное время.

В простейшем случае реактор периодического действия состоит из сосуда с мешалкой, которая обеспечивает такое интенсивное перемешивание среды, при котором концентрация во всем объеме в любой момент времени одинакова. Теплообмен осуществляется через рубашку или змеевик.

Состав реакционной массы меняется со временем, а поэтому скорость реакции изменяется в течение процесса.

Как видно из рисунка 177 с течением времени концентрация реагента А уменьшается от начального значения до значения , соответствующего требуемой степени превращения. Так как на единицу объема реагирует - из общего количества молей, то глубина превращения может быть определена как

, (12.7)

Время пребывания реагента в реакторе можно найти следующим образом. Обозначим через - объем реакционной массы, - число молей реагента А.

Процесс протекает во времени. Тогда по материальному балансу для исходного компонента А найдем.

, (12.8)

где r - скорость реакции, с^-1.

Поскольку

, (12.9)

То с учетом выражения (12.9) уравнение материального баланса (2.8) заменяется

, (12.10)

или

, (12.11)

В общем случае для реакции любого n-ого порядка скорость реакции r с учетом выражения (12.7) можно представить

, (12.12)

И тогда уравнение (12.11) примет вид:

, (12.13)

Выражая через степень превращения получим

, (12.14)

Подставив найденное значение из (12.14) в (12.13) будем иметь

, (12.15)

Или после деления левой и правой части на С

, (12.16)

После интегрирования выражения (12.16) время пребывания реагентов в реакторе равно

, (12.17)

при получим

, (12.18)

при n=1

, (12.19)

Примеры расчетов показателей процесса: степени превращения, конверсии и т.п.

Описание: Определить степень конверсии реагентов если уравнение процесса таково: 25СН2=СН216Н2О→С2Н5ОН24СН2=СН215Н2О Решение. Определить селективность процесса. Определить объем этиленовой фракции если объемная доля этилена в ней равна 90 необходимый для получения 810 кг этилхлорида. Определить вместимость реактора приняв для расчета константы скорости формулы: Решение.

Пример 1. Определить степень конверсии реагентов, если уравнение процесса таково:

25СН₂=СН₂+16Н₂О→С₂Н₅ОН+24СН₂=СН₂+15Н₂О

Решение. Количество превращенных реагентов

Этилен 25-24 = 1 моль

Вода 16-15 = 1 моль

Степень конверсии реагентов:

Этилен 1 : 25 = 0,04, или 4%

Вода 1 : 16 = 0,0625, или 6,25%

Пример 2. Пиролизу подвергли 1500 м³ метана. Степень конверсии метана равна 60%, масса ацетилена в продуктах пиролиза составляет 400 кг. Определить селективность процесса.

Решение. Уравнение реакции:

2СН₄ → С₂Н₂ + 3Н₂

2∙22,4 м³   26 кг.  3∙2 кг

Объем превращения метана:

1500 ∙ 0,6 = 900 м³

Теоретически возможную массу ацетилена (в расчете на превращенный метан) определяют, исходя из стехиометрических соотношений по пропорции:

2∙22,4 м³ С₄ – 26 кг С₂Н₂

900 м³ СН₄ – m кг С₂Н₂

Откуда

Селективность процесса:

400 : 522 = 0,766 или 76,6%

Пример 3. Выход этилхлорида, получаемого гидрохлорированием этилена, составляет 90% от теоретического. Определить объем этиленовой фракции, если объемная доля этилена в ней равна 90%, необходимый для получения 810 кг этилхлорида.

Решение. Уравнение реакции:

С₂Н₄ + НCL → С₂Н₂CL

22,4 м³  36,5 кг  64,5 кг

Максимально возможную (теоретическую) массу этилхлорида определяют с учетом выхода продукта:

810 : 0,9 = 900 кг С₂H₂Cl

Объем этилена исходя из стехиометрических соотношений:

22,4 ∙ 900 : 64,5 = 312 м³ С₂Н₄

Объем этиловой фракции:

312,6 : 0,9 = 347,3 м³

1.  Элементы расчетов химических реакторов

Расчет реактора для провидения химического взаимодействия является основной частью технологического расчета производства. Этот расчет сводится к определению основных конструктивных размеров аппаратов и их числа. Размеры и число аппаратов как периодического, так и непрерывного действия определяются их производительностью.

Производительность реакционного аппарата или установки – количество целевого продукта (кг, т, м²), получаемого в единицу времени (с, ч, сутки, год). Зафиксированная производительность аппарата установки называется мощностью.

Объем рабочей части (реакционной зоны) аппаратов непрерывного действия определяют по уравнению:

где – N_c – секундная объемная производительность (м³/с). а τ – время, необходимое для проведения процесса, с.

Площадь поперечного сечения аппарата составляет (в м²):

где ω – скорость течения среды в аппарате, м/с.

Определив площадь сечения, легко найти диаметр аппарата (в м):

Высота (длина) реакционной зоны аппарата равна (в м):

Для аппаратов, заполненных катализатором, объем рабочей части равным объему катализатора V_к (м³), который определяют исходя из объемной скорости газа (жидкости) или производительности катализатора.

Объемная скорость – объем газовой смеси( жидкости), проходящей через единицу катализатора в единицу времени [м³/ (м³∙ч) или ч^-1]:

Откуда

Производительность катализатора – масса (объема) целевого продукта снимаемого с единицы объема (массы) катализатора в единицу времени [кг/ (м³∙ч), м³/ (м³∙ч), кг/(кг∙ч), м³/ (кг∙ч)]:

 

Для периодических процессов общей реакционный объем аппаратов равен (в м³):

где V_сут – суточный объем перерабатываемых веществ,

      τ – время технологического цикла (на проведение собственно процесса и вспомогательных операций), κ_зап – коэффициент заполнения аппарата (принимается от 0,4 до 0,9).

В специальной литературе описаны конструкции реакторов для многочисленных химических процессов, их собственности и методов расчета, поэтому ограничимся здесь некоторыми сведениями по элементам расчета реакторов, не имеющих прототипа.

Выбор конструкции промышленного реактора зависит прежде всего от следующих параметров: скорости протекания химических реакций (от времени пребывания в реакционной зоне), оптимальных условий тепло - и массобмена и оптимальных температуры и давления. Так как на практике сложно удовлетворить все требования, предъявляемые к промышленному реактору, то определяющими являются экономические показатели.

Для расчета химического реактора используют их идеализированные модели, среди которых выделяют:

а) периодический реактор полного смешения;

б) непрерывный реактор идеального вытеснения;

в) непрерывный реактор полного смешения.

Известно, что химические реакции могут протекать в диффузионной, кинетической или переходной области, но в общем случае скорость химико-технологического процесса можно выразить уравнением и=κ∆С, где и – скорость процесса, κ – константа скорости, а ∆С движущая сила процесса.

В технологии основного органического и нефтехимического синтеза многие процессы осуществляют непрерывно, следовательно, достижение максимального выхода продукта определяется временем пребывания реагирующих веществ в реакционной зоне. Отсюда следует, что необходимая вместимость реакционного аппарата, его производительность и интенсивность работы зависит от скорости провидения процесса.

Время пребывания реагирующих  веществ реакционной зоне (τ) определяют из кинетических уравнений первого, второго и третьего порядков. В реакциях первого порядка стехиометрический коэффициент прямой реакции равен единицы, в реакции второго порядка – двум, третьего – трем. Так как стехиометрические коэффициенты химического уравнения не всегда определяют порядок реакции, то его устанавливают экспериментально. Для реакции первого порядка:

Для реакции второго порядка:

В случае равенства концентрации двух веществ кинетическое урвнение для второго порядка упрощается :

Для реакции третьего порядка имеем:

Где τ – время реакции, с; κ^’, κ^’’, κ^’’’ - соответственно константы скорости реакции первого, второго и третьего порядка, с^-1, л/ (моль∙с); a и b – начальные концентрации веществ, моль/л; x – количество вещества, вступившего в реакцию к моменту времени τ, моль/л.

Пример 4. Производительность реактора дегидрирования н-бутана до н-бутенов составляет 17400 кг целевого продукта в час. Процесс проводят при 600⁰С, и в этих условиях степень конверсии н-бутана равна 30%, а селективность по н-бутенам составляет 75%. Определить вместимость реактора, приняв для расчета константы скорости формулы:

Решение. Уравнение реакции:

СН_3­ – СН₂ – СН₂ – СН₃ ↔ СН₂ = СН – СН₂ – СН₃ + Н₂

58 кг (22,4 м³)     56 кг        2 кг

Расход н-бутана для проведения процесса:

или 30933 : 3600 = 8,6 м³/с

Константа скорости:

Вместимость реактора:

V_p = 8,6 ∙ 2,2 = 19 м³

Пример 5. Акрилонитрил получают окислительным аммонолизом пропилена в псевдоожиженном слое катализатора. В реактор, производительность которого по целевому продукту равна 5600 кг/ч, поступает газовая смесь, объемная доля пропилена в которой 8%. При 450⁰С степень конверсии пропилена равна 60%, а селективность по акрилонитрилу составляет 75%. Определить объем катализатора в реакторе, приняв для расчета константы скорости такую формулу:

k = 2,8 ∙ 10⁵ e^-80000/RT

Решение. Уравнение реакции:

СН_2­ = СН – СН₃ + NH₃ + 1,5O₂ → CH₂ = CHCN + 3H₂O

 42 кг (22,4 м³) 17 кг   15∙32 кг   53 кг      3∙18 кг

Расход пропилена на проведение процесса:

Объемный расход газовой смеси на входе в реактор:

Определение константы скорости:

k = 2,8 ∙10⁵ ∙ 2,72^{-80000/8,314(450+273)­} = 2,8 ∙ 10⁵ ∙ 2,72^-13,3 = 2,8 ∙ 10⁵ ∙ 0,2 ∙ 10^-5 = 0,56 с^-1

где R=8,314 кДж/(моль∙К), а e=2,72.

При соотношении исходных веществ С₃Н₆ : NH₃ : O₂ : H₂OЮ равном 1: 0,7 : 1,7 : 3, реакция окислительного аммонолиза имеет первый порядок по пропилену, а по кислороду и аммиаку – нулевой.

Формула для расчета времени пребывания веществ в реакционной зоне :

Объем катализатора в реакторе:

18,3 ∙ 1,65 = 30 м³

Пример 6. Время пребывания углеводородов при получении ацетилена электрокрекингом равно 0,001 с, объемный расход газов пиролиза равен 25500 м³/ч, скорость газов в реакционной камере составляет 900 м/с. определить площадь сечения, высоты и объем реакционной камеры электродугового реактора.

Решение. Секундная объемная производительность реактора (по газам электрокрекинга) :

25500 : 3600 = 7,08 м³/с

Объем реакционной камеры:

7,08 ∙ 0,001 = 0,0071 м³

Площадь сечения реакционной камеры:

7,08 : 900 = 0,0079 м²

Высота реакционной камеры:

0,0071 : 0,0079 = 0,9 м или 900 ∙ 0,001 = 0,9 м

Пример 7. Объемная скорость подачи этилена в реактор прямой гидратации равна 1900 ч^-1, а объемный расход этилена составляет 22000 м³/ч. Определить объем катализатора, необходимый для проведения процесса.

Решение. Объем катализатора:

22000 : 1900 = 11,6 м³

Пример 8. Производительность реактора окисления метанола составляет 3500 кг формалина в час; массовая доля формальдегида в нем равна 37%. Диаметр сечения аппарата 1,4 м, высота слоя контактной массы 75 мм. Определить производительность 1 кг и 1л контактной массы. Насыпная плотность катализатора равна 600 кг/м³.

Решение. Производительность реактора по целевому продукту – формальдегиду:

3500 ∙ 0,37 = 1295 кг/ч

Объем катализатора в реакторе (V=πD²H/4 = 0,785 D² H) :

0,785 (1,4)² ∙ 0,075 = 115 м³ или 115 л

Производительность 1 л катализатора:

1295 : 115 = 11,3 кг/(л∙ч)

Масса катализатора в реакторе:

0,115 ∙ 600 = 69 кг

Производительность 1 кг катализатора:

1295 : 69 = 18,8/(кг∙ч)

Реактор идеального смешения непрерывного действия

Схема потоков в реакторе полного смешения представлена на рис. 1. В реакторе такого типа концентрация любого компонента равномерна по всему реакционному объему, и поэтому уравнение материального баланса можно записать для всего объема реактора. Для установившегося режима:

G_пр= G_ух+ G_хр (1),

где G_пр – масса вещества, поступающего в элементарный объем в единицу времени; G_ух - масса вещества, выходящего из элементарного объема в единицу времени; G_хр – скорость расходования исходного вещества в результате химической реакции, протекающей в элементарном объеме:

(2); (3). Так как степень превращения равна: (4); (5); то (6),

Рис.1. Схема реактора идеального смешения.

где, - начальная концентрация исходного вещества, - конечная концентрация исходного вещества, - объемный расход реакционной смеси, - скорость химической реакции, - время химической реакции,

-степень превращения, V- объем реакционной смеси.

Уравнение (5, 6) представляют собой проектные уравнения реактора идеального смешения и позволяют определить неизвестную величину по заданным. В любом случае для реактора идеального смешения его размер, расход реагентов, начальные и конечные концентрации могут быть определены только при условии, если известна кинетика процесса.

В таблице 1 приведены расчетные уравнения для реактора идеального смешения непрерывного действия при проведении в нем простых обратимых и необратимых, а также сложных химических реакций.

Таблица 1. Расчетные уравнения для РИС-Н

Схема реакции	Кинетическая модель	Расчетные уравнения
	при

Рассмотрим некоторые примеры расчета такого типа реакторов.

Пример 9.

Определить объем реактора идеального смешения для реакции протекающего без изменения объема реакционной массы.

Дано:

реакция А → 2S;

порядок реакции n=1;

объемный расход исходного вещества G_V = 0,25 л/мин;

начальная концентрация исходного вещества С_А0= 0,5 моль/л;

константа скорости реакции k= 0.15 мин ^-1;

степень превращения x_A = 0,52.

Решение.

Так как реакция первого порядка, скорость реакции определяем по уравнению:

.

В РИС-Н приравниваем объем реакционной массы к объему реактора, тогда по уравнению:

Пример 10.

Определить объем реактора идеального смешения для обратимой реакции протекающего без изменения объема реакционной массы.

Дано:

реакция 2А ↔R+S;

порядок реакции n=2;

объемный расход исходного вещества G_V = 4,8 м³/ч;

начальная концентрация исходного вещества С_А,0= 1,5 кмоль/м³;

константа скорости прямой реакции k₁ = 2*10-3 м³/(кмоль∙с);

константа равновесия Кр = 9;

требуемая степень превращения x_A = 0,8 от равновесной.

Решение.

Объем реактора, в котором проводится данная реакция, определяем из базового уравнения для РИС-Н:

; .

Так как реакция обратимая, составляем кинетическую модель для данной реакции:

т.к. и .

С учетом вышеизложенного выражаем время реакции:

,

где - фактическая степень превращения;

- константа скорости обратной реакции.

В этом уравнении неизвестными величинами являются фактическая степень превращения и константа скорости обратной реакции. Константу скорости обратимой реакции определяем из уравнения:

.

Для определения равновесной степени превращения используем константу равновесия, выраженную через концентрации веществ:

,

где -равновесная степень превращения.

Подставляя в данное выражение значения константы равновесия, получаем . Так как требуемая степень превращения равна 0,8, то фактическая степень превращения будет равна:

.

Тогда время реакции будет равно:

.

С учетом полученного времени реакции объем реактора составит: