Теория вероятности Комбинаторика

Соединения:

1. Перестановка: P_n=n!

2. Сочетания:

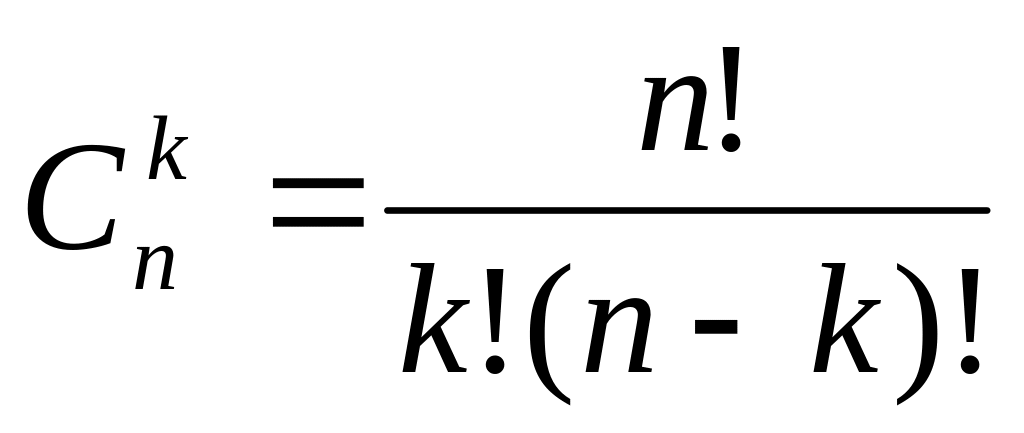
3. Размещения:

Свойства сочетаний:

1.

2.

3.

4. 0! = 1; 1!=1.

Сумма событий А и В – такое событие С, которое состоит в появлении или А, или В, или и А, и В одновременно: А+В=С=А В.

Произведение событий А и В – такое событие С, которое состоит в том, что появляется и А, и В одновременно.

Законы:

1. (А+В)*С=АС+ВС – ассоциативный закон.

2. А*В=В*А; А+В=В+А – коммутативный закон.

События А_j составляют полную группу событий, если они попарно несовместны и в опыте одно из них обязательно произойдет:

1. А_i*A_j=Ø i, j

2. A₁+A₂+…+A_n=

Относительная частота события:

W(A)=m/n

Классическое определение вероятности:

P(A)= W(A)=m/n

События равновозможные, если в условиях опыта ни одно из этих событий не является более вероятным, чем др.

Единовозможные события – события, кроме которых не могут произойти никакие др.

Геометрическое определение вероятности:

P(g)=mesg/mesG

Аксиомы ТВ:

1. Р(А) 0

2. P( )=1

3. P(Ø)=0

4. P(A+B)=P(A)+P(B), А, В – несовместные.

Зависимые события А и В – это события, вероятность одного из которых меняется в зависимости от того, произошло др. событие или нет, в противоположном случае они независимы.

Условной вероятностью называется вероятность события В при условии, что событие А наступило:

P_A(B)=P(AB)/P(A)

Теорема умножения вероятностей:

P(AB)=P(A)*P_A(B) – вероятность появления 2-х событий А и В равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что 1-ое событие уже наступило.

P(AB)=P(A)*P_A(B)=P(B)*P_B(A)

Если А и В независимы Р(АВ)=Р(А)*Р(В).

Если 3 события А, В, С независимы Р(АВС)=Р(А)*Р(В)*Р(С).

Если А, В, С зависимы Р(АВС)=Р(А)*Р_А(В)*Р_АВ(С).

Несколько событий называются попарно независимыми, если каждые 2 из них независимы.

Несколько событий независимы в совокупности, если независимы каждые 2 из них и независимы каждое событие и все возможные произведения остальных.

Теорема сложения:

Вероятность появления одного из нескольких попарно независимых событий равна сумме вероятностей этих событий:

P(A₁+…+A_n)= .

.

Вероятность появления хотя бы одного из п событий независимых в совокупности равна разности между единицей и произведением вероятности противоположных событий:

.

Два события называют совместными, если появление одного из них не исключает появление другого в одном и том же испытании.

Теорема. Вероятность появления хотя бы одного из 2-х совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления:

Р(А+В)=Р(А)+Р(В)-Р(АВ).

Независимые события:

Р(АВ)=Р(А)*Р(В)

Р(А+В)=Р(А)+Р(В)-Р(А)*Р(В).

Зависимые события:

Р(А+В)=Р(А)+Р(В)-Р(А)*Р_А(В).

Несовместные события:

А*В=Ø и Р(АВ)=0 → Р(А+В)=Р(А)+Р(В).

Формула полной вероятности

Теорема. Вероятность события А, которое может наступить при условии появления одного из несовместных событий В₁, В₂,…,В_п, образующих полную группу, равна сумме произведений вероятностей каждого из этих событий на соответствующую условную вероятность события А:

P(A)=