35. Дискретные случайные величины. Ряд распределения и функция распределения вероятностей
Случайная величина- это переменная величина, конкретное значение которой зависит от случая .
Непрерывную случайную величину А следует задавать не указанием вероятностей ее отделных значений, а неприрывной функцией, называемой плотностью распределения вероятностей случайной величины А. непрерывная величина- величина постоянная. Для нее плотность распределения - максимум
Дискретная
случайная величина – количественный
признак, который проявляет себя в виде
изолированный числовых значений.
Например - количество солнечных дней в
году. Число опрошенных на занятии.
Законом распределения ДСВ. Называют
таблицу из двух строк. В верхней -
значения. В нижней- вероятности этих
значений. Следует заметит что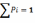 
.
Ф-ция
распределения случайных величин 
называется функция действительного
аргумента x равная вероятности того,
что случайная величина 
примет значение меньше чем x.
СВОЙСТВА:
Функция
распределения является ограниченной
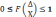
Функция распределения является неубывающей или постоянной.
Предел функции распределения при х стремится к
Вероятность попадания случайных величин в полуинтервал ав= разноси значений.
СВОЙСТВА:
Функция распределения является ограниченной
Функция распределения является неубывающей или постоянной.
Предел функции распределения при х стремится к
Вероятность попадания случайных величин в полуинтервал ав= разноси значений.
36. Числовые характеристики дискретных случайных величин.
1.Математическое
ожидание (МО)
- сумма произведений всех возможных
значений случайной величины на их
вероятности. Это некоторый центр, вокруг
которого группируются остальные значения
случайной величины.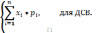
Свойства МО: 1)МО постоянной величины равно самой постоянной : М(С) = С. 2)Постоянный множитель можно выносить за знак МО: М(СХ) = СМ(Х). 3)МО произведения двух независимых случайных величин равно произведению их математических ожиданий: M(XY) = M(X) * M(Y).
4)МО суммы двух случайных величин равно сумме математических ожиданий слагаемых: M(X+Y) = M(X)+M(Y).
2. Дисперсия. Дисперсией случайной величины называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания: D[X] = M[(X – M[X])].
Свойства дисперсии: 1)Дисперсия постоянной величины равна нулю: D(C)=0. 2)Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат: D(CX) = C²D(X). 3)Дисперсия суммы равна сумме дисперсий: D(X+Y) = D(X)+D(Y). 4)Дисперсия разности равна сумме дисперсий: D(X-Y) = D(X)+D(Y).
3. Среднее квадратическое отклонение.Средним квадратическим отклонием (СКО) случайной величины Х называется квадратный корень из дисперсии: σ(Х) = √ D(X).
4. Мода. Модой М0 дискретной случайной величины называется ее наиболее вероятное значение. Для непрерывной случайной величины мода – такое значение случайной величины, при которой плотность распределения имеет максимум: f(M0) = max.
Если случайная функция распределения имеет несколько максимумов, то такое распределение называется двухмодальным или многомодальным. сли распределение имеет минимум, но не имеет максимум. То оно называется антимодальным.
5. Медиана. Медианой Ме случайной величины Х называется такое ее значение, относительно которого равновероятно получение большего или меньшего значения случайной величины: P(X<Me) = P(X>Me).