2.9.5 Организация данных на основе использования в-деревьев
2.9.5.1 Терминология и разновидности графов типа «дерево»
Понятие графа типа «дерево» введено нами ранее при рассмотрении иерархической модели данных (см. п. 2.1) как варианта их логической организации. При рассмотрения вопросов физической организации данных на ВЗУ также используется понятие древовидного графа или дерева.
На рис. 2.18приведен пример дерева и общие термины, используемые при описании деревьев.
Диаграмма дерева из примера имеет высоту 4 (число уровней), момент 22 (число узлов), вес 16 (число листьев), основание 1 (число корней).
Рис. 2.18. Общие термины: используемые при описании деревьев.
Иногда используется термин сбалансированное дерево.В таком дереве каждый узел имеет одинаковое число ветвей, причем процесс включения новых ветвей в узлы дерева идет сверху вниз, а на каждом уровне дерева —слева направо. На рис. 2.19показаны примеры сбалансированных и несбалансированных деревьев.
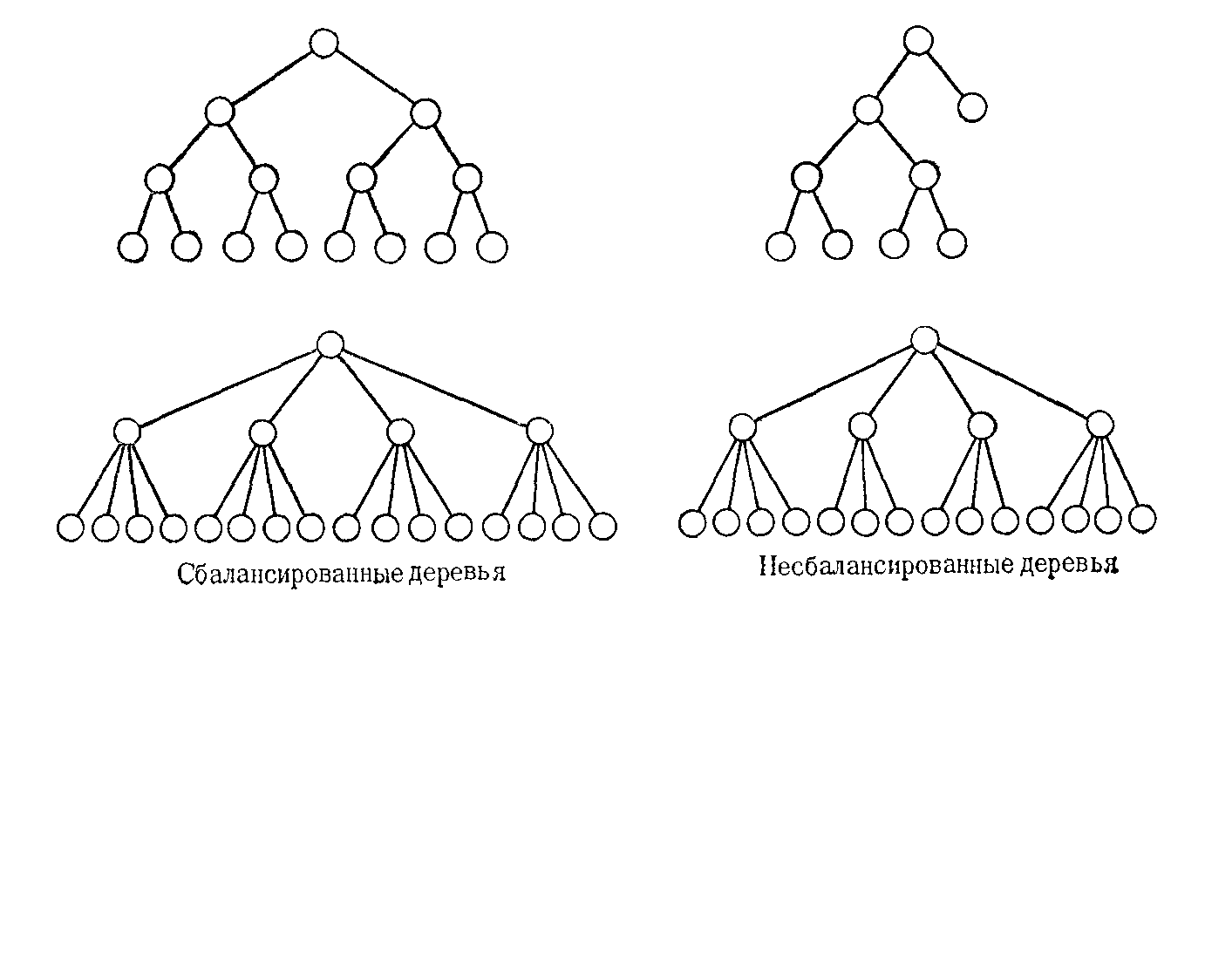
Рис. 2.19. Сбалансированные и несбалансированные деревья.
Логическая организация данных, как правило, не может быть задана в виде сбалансированной древовидной структуры, чаще требуется переменное число ветвей в каждом узле. Физическая организация данных оказывается более простой для дерева с фиксированным число ветвей, чем для дерева с переменным числом ветвей. В частности, индексы могут быть представлены в виде сбалансированных древовидных структур.
Имеется особая категория древовидных структур, в которой допускается не более двух ветвей для одного узла. Такая структура называется двоичным деревом.На рис. 2.20показано несбалансированное двоичное дерево,
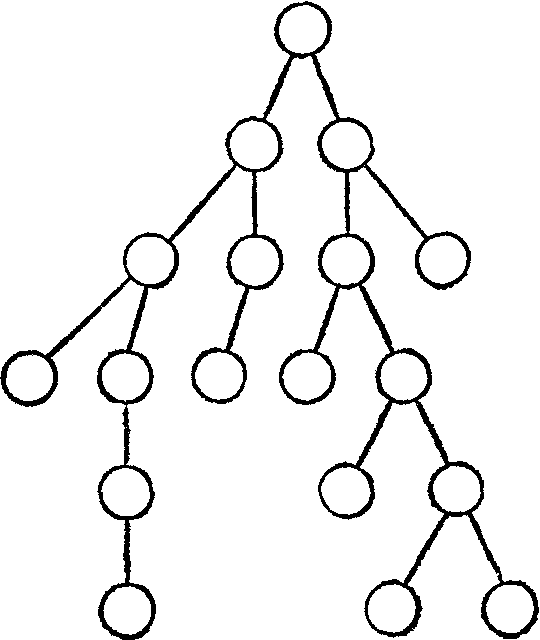
Рис. 2.20. Несбалансированное двоичное дерево
Любые связи в дереве можно представить в виде двоичных древовидных структур (рис. 2.21).
Рис. 2.21. Представление древовидной структуры в виде двоичного дерева,
в котором каждый элемент может иметь указатели
как на порожденные, так и на подобные элементы
2.9.5.2 Индексирование на основе в-деревьев
На основе В-деревьев реализуется простая идея построения индекса над уже построенным индексом. Действительно, если построить неплотный индекс (см. п.2.9.4.2), то сама индексная область может быть рассмотрена как основной файл, над которым надо снова построить неплотный индекс, а потом снова над новым индексом - следующий и так до того момента, пока не останется всего один индексный блок.
Мы в общем случае получим некоторое дерево, каждый родительский блок которого связан с одинаковым количеством подчиненных блоков, число которых равно числу индексных записей, размещаемых в одном блоке. Количество обращений к диску при этом для поиска любой записи одинаково и равно количеству уровней в построенном дереве. Такие деревья, как мы знаем, называются сбалансированными (balanced) именно потому, что путь от корня до любого листа в этом дереве одинаков. Именно термин «сбалансированное» от английского «balanced» — «сбалансированный, взвешенный» и дал название данному методу организации индекса.
Построим подобное дерево для примера из п. 2.9.4 и рассчитаем для него количество уровней и, соответственно, количество обращений к диску.
На первом уровне число блоков равно числу блоков основной области, это нам известно, — оно равно 12500 блоков. Второй уровень образуется из неплотного индекса, мы его тоже уже строили и вычислили, что количество блоков индексной области в этом случае равно 172 блокам. А теперь над этим вторым уровнем снова построим неплотный индекс.
Мы не будем менять длину индексной записи, а будем считать ее прежней, равной 14 байтам. Количество индексных записей в одном блоке нам тоже известно, и оно равно 73. Поэтому сразу определим, сколько блоков нам необходимо для хранения ссылок на 172 блока.
KIB3=KIB2/KZIB= 172/73 = 3 блока
Мы снова округляем в большую сторону, потому что последний, третий, блок будет заполнен не полностью.
И над третьим уровнем строим новый, и на нем будет всего один блок, в котором будет всего три записи. Поэтому число уровней в построенном дереве равно четырем, и соответственно количество обращений к диску для доступа к произвольной записи равно четырем (рис.2.22). Это не максимально возможное число обращений, а всегда одно и то же, одинаковое для доступа к любой записи.
Тд=Rуровней=4
уровень 12500 блоков
уровень 172 блоков
уровень 3 блоков
уровень 1 блоков
Рис. 2.22 Построенное В-дерево
Механизм добавления и удаления записи при организации индекса в виде В-дерева аналогичен механизму, применяемому в случае с неплотным индексом.