26.Количество информации

Количество информации – это числовая характеристика информации, отражающая ту степень неопределенности, которая исчезает после получения информации. За единицу количества информации принимается один бит.

Бит – слишком маленькое количество информации. На практике чаще применяются более крупные единицы, чтобы измерить количество информации, например байт, являющийся последовательностью из восьми бит. Именно восемь битов или один байт, используется для того, чтобы закодировать символы алфавита. Один байт также является минимальной единицей адресуемой памяти компьютера, т.е. обратиться в память компьютера можно к байту, а не к биту.

1 килобайт – 1024 байт

1 мегабайт – 1024 кб

…

27. Скорость передачи информации и пропускная способность каналов связи

В условиях отсутствия помех скорость передачи информации определяется количеством информации, переносимым символом сообщения в единицу времени и равна

(5.1)

n – количество символов, вырабатываемых источником сообщения за единицу времени.

H – энтропия, снимаемая при получении одного символа сообщения.

Техническая скорость передачи

( симв/сек ) , (5.2)

где 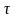- время передачи одного символа вторичного алфавита.

Таким образом, для сообщений, составленных из равновероятных взаимонезависимых символов равной длительности скорость передачи информации

( бит/сек ).

В случае неравновероятных символов равной длительности

( бит/сек )

Пропускная способность ( или емкость канала связи ) есть максимальная скорость передачи информации по данному каналу связи:

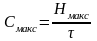( бит/сек ).

28.Потери в канале связи

При неравной вероятности появления символов (формула Шеннона) количество информации, содержащееся в сообщении заданной длины (n), снижается. Другим фактором, снижающим энтропию, а, следовательно, и количество информации в сообщении заданной длины (n), является наличие статистической зависимости между символами – корреляции.

Из-за корреляционных связей между символами и неравновероятного их появления количество информации в реальных сообщениях падает. Количественно эти потери информации характеризуются коэффициентом избыточности (R)

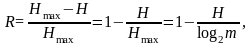(1.11)

где — максимальное количество информации, которое может содержать один символ сообщения, определяемое по формуле (1.6);

1. Н — среднее количество информации, которое переносит один символ в реальных сообщениях;

m — число символов в алфавите источника сообщений (объём алфавита).

Средняя скорость передачи (скорость передачи) характеризует среднее количество информации, передаваемое по каналу в единицу времени. Этот показатель тоже зависит от наличия шумов и помех. В любом реальном канале связи всегда имеют место помехи и искажения как детерминированного, так и случайного характера, что ведет к потере информации в канале. Действительно, если на передающем конце канала количество информации, приходящейся на один символ сообщения равно I₁, то вследствие воздействия шума после прохождения канала на один символ принятого сообщения будет приходиться количество информации равное I₂, причем

I2 = I1 – ΔI ,

где ΔI представляет собой количественную меру потери информации при передаче одного символа. Так как среднее количество информации, переносимое одним символом по каналу с шумом, уменьшается, то, очевидно, что снижается и пропускная способность канала с шумом по сравнению с каналом без шумов.