24. Дифференциальная энтропия и ее свойства

Дифференциальная энтропия- часть энтропии источника непрерывных сообщений, которая зависит от плотности вероятности сигнала x(t), выдаваемого источником.

Свойства диффенециальной энтропии:

1.Дифференциальная  энтропия не может служить  абсолютной мерой неопределенности  непрерывного источника. Однако  при сравнении, например, абсолютных  энтропий  различных источников, энтропий отсчетов сигналов на входе и выходе канала связи и т. д. второе слагаемое в выражении при вычислении соответствующих разностей сокращается, и информационные свойства полностью определяются разностью соответствующих дифференциальных энтропий (отсюда и название – дифференциальная энтропия). 2. Дифференциальная  энтропия является относительной  мерой неопределенности, и ее  значение зависит от масштаба  случайной величины U, а следовательно, и от выбора единиц ее измерения. 

3. Дифференциальная  энтропия, в отличие от энтропии  дискретного источника, наряду  с нулевыми и положительными  значениями также может принимать  и отрицательные значения. 4) Дифференциальная  энтропия не изменяется, если  к случайной величине U прибавить некоторую постоянную величину c

25.Эпсилон-энтропия случайной величины

1.7. Эпсилон-энтропия случайной величины

Воспринимающие информацию датчики, включая человека, обладают ограниченной чувствительностью и конечной разрешающей способностью, а также тем, что процесс восприятия сопровождается помехами.

   Если учесть, что нас интересует приближенное восприятие реализации, то количество информации, приходящееся на отсчет или на единицу времени, можно вычислить.

   Ограничимся рассмотрением простейшего случая, когда отдельные состояния источника информации представляют собой независимые реализации случайной величины U. (Эпсилон-энтропия случайного процесса рассмотрена в ? 4.4.)

   Ансамбль реализации случайной величины U описывается плотностью распределения вероятностей р(u). О значениях случайной величины U можно судить по значениям другой случайной величины Z, если мера их различия не превышает заданной верности воспроизведения. В этом случае говорят, чти Z воспроизводит U.

   Для количественной оценки степени сходства сигналов целесообразно ввести какую-либо функцию р(z, u), имеющую природу ?расстояния?. Тогда удобным критерием верности V(Z, U) является среднее значение функции р(z, u), взятое по всему множеству значений z и u

 (1.59)

где. р(z, u) - плотность совместного распределения вероятностей величии Z и U.

   Наиболее широко используется среднеквадратический критерий, при котором р(z, u) представляет собой квадрат обычного евклидова расстояния между точками в соответствующем пространстве (см. ? 2.12).

   Требование к верности в данном случае задается с использованном критерия V(ZU):

 (1.60)

где p_u(z) -- условная плотность распределения - функция правдоподобия того, что конкретный сигнал и будет

воспроизведен как сигнал z; e - заданное значение верности.

   Так как плотность р(u) определена, то для выполнения условия (1.60) варьировать можно только условной плотностью распределенияр_u(z).

   Если случайная величина Z воспроизводит случайную величину U с некоторой верностью e , то количество информации, содержащееся в воспроизводящей величине Z относительно U, конечно и в соответствии с (1.54) может быть записано в форме

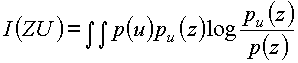 (1.61)

где  - плотность воспроизводящей величины Z.

   Желательно обеспечить заданную мерность воспроизведения при минимальном количестве получаемой информации. Поэтому среди множества функций р_u(z), удовлетворяющих условию (1.60), целесообразно выбрать такую, которая обеспечивает наименьшее I(ZU)[10,35].

   Минимальное количество информации в одной случайной величине Z относительно другой U, при котором удовлетворяется заданное требование к верности воспроизведения величины U, называется e-энтропией величины U и обозначается H_e(U):

 (1.62)

при

 (1.63)

   Используя безусловную h(U) и условную h_z(U) дифференциальные энтропии величины U, выражение (3.63) можно представить в виде

 (1.64)

где p_Z(U) - условная плотность вероятности того, что в теx случаях, когда был принят сигнал z, передавался сигнал u.

Пример 1.9. Найти H_e(U) источника информации, ансамбль состояний которого описывается нормально распределенной случайной величиной U с дисперсией s² при вероятности воспроизведения V'(ZU)<e².

Будем считать, что заданная верность воспроизведения обусловлена действием аддитивной статистически не связаннной с сигналом

помехой Е, причем М[E] = 0 и M [E^{2] =} e². Передаваемый сигнал u рассматриваем как сумму воспроизводящего сигнала z и помехи u = z + x

Так как в данном случае h_z(U) в выражении (3.64) полностью определяется помехой [h_z(U) = h_z(Z+E) = h(E)], то H_{E(U) = h(U) - max h(E),}

где h(E)-дифференциальная энтропия помехи; р(x) - плотность распределения помехи Е.

Ранее [см. (1.41)] нами установлено, что при ограничении на дисперсию случайной величины максимальной дифференциальной энтропией обладает нормальное распределение. Поэтому в соответствии с (1.42) получаем

откуда,

 (1.65)

Так как s² определяет среднюю мощность Р_u сигнала, а e² - среднюю мощность р_x, помехи E, то выражение (3.65) характеризует зависимость эпсилон-энтропии от величины Р_u/Р_x, называемой отношением cигнал / помеха.

При заданном отношении сигнал/помеха значение H(U) для нормально распределенной случайной величины является максимально возможным.

Для произвольно распределенной случайной величины U при том же критерии верности и малых e [ когда Н_e(U) велико] справедливо приближенное равенство

 (1.66)