54. Технические средства кодирования и декодирования для групповых кодов. Циклическое кодирование

Важное место среди систематических кодов занимает циклические коды. Свойство цикличности состоит в том, что циклическая перестановка всех символов кодовой комбинации Аі дает другую кодовую комбинацию Ај, также принадлежащую этому коду. При такой перестановке символы кодовой комбинации перемещаются слева направо на одну позицию, причем крайний правый символ переносится на место крайнего левого символа. Например, Аі =101100 және Аj=010110 немесе Аі =011101 және Аj=101110. Комбинация циклического кода, выражаемые двоичными числами, для удобства преобразований обычно определяют в виде полиномов, коэффициенты котроых равны 0 или 1. Примером этого может служить следующая запись: А(z)=10011=1·z

Помимо цикличности кодовые комбинации обладают другим важным свойством. Если их представить в виде полиномов, то все они делятся без остатка на так называемый порождающий полином G(z) степени r=n-k, где k-значность первичного кода без избыточности, n-значность циклического кода. Построение комбинаций циклических кодов возможно путем умножения комбинации первичного кода А*(z) на порождающий полином G(z): A(z)=A*(z)·G(z).

Умножение производится по модулю z и в данном случае сводится к умножению по обычным правилам с приведением подпбных членов по модулю два. В полученной таким способом комбинации A(z) в явном виде не содержатся информационные символы, однако они всегда могут быть выделены в результате обратной операции: A(z) на G(z).

Другой способ кодирования, позволяющий представить кодовую комбинацию в виде информационных и контрольных символов, заключается в следующем. К комбинации первичного кода дописывается справа r нулей, что эквивалентно поаышению полинома А*(z) на m разрядов, т.е. умножению на z. Затем z· А*(z) делится на порождающий полином. В общем случае результат деления состоит из целого числа Q(z) и остатка R(z). Отсюда:

z· А*(z)=Q(z)G(z)○R(z)

55. Квантование информации

Непрерывные сигналы в системе обобщенных координат X, T, описываются непрерывными функциями x(t). Переход от аналогового представления сигнала к цифровому связан с квантованием (дискретизацией) сигнала x(t) по времени и по уровню.

Применяется при передаче, хранении и обработке информации.

56. Классификация методов дискретизации

Классификация методов дискретизации может быть проведена по следующим признакам.

* квантование по времени – дискретизация;

ость

1. регулярность отсчетов;

2. критерий оценка точности дискретизации и восстановления;

3. базисные функции;

4. принцип приближения;

1. Регулярность отсчетов:

По регулярности отсчетов методы дискретизации делятся на равномерную и неравномерную.

равномерные;

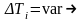неравномерные.

(адаптивные и программируемые).

При адаптивных методах интервал изменяется в зависимости от текущего изменения параметров реализации сигналов. При программируемых методах изменение интервалов (частота опроса F₀) производится либо оператором на основании анализа поступающей информации, либо в соответствии с заранее установленной программой работой.

Критерий оценки точности

Пусть значение сигнала x(t),а воспроизводящей функции V(t) ,тогда погрешность 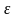(t) дискретизации или соответственно восстановления:

Оценка погрешности может производиться как для отдельных, так и для множества реализации сигнала.

Наиболее часто отклонение воспроизводимой функции V(t) от сигнала x(t) на интервале оценивается следующими критериями.

1. Критерий наибольшего отклонения

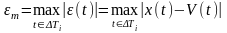
2. Среднеквадратический критерий

3. Интегральный критерий как мера отклонения x(t) от V(t) имеет вид:

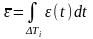
4. Вероятностный критерий определяется соотношением

– допустимое значение погрешности;

p₀ – допустимая вероятность того, что погрешность не превышает значения .

2) Базисные функции

Формулировка задачи дискретизации следующая: для данной x(t), принадлежащей классу R функции, определенных на отрезке [a,b], найти функцию p(t) или V(t) S, (где S – некоторый выстроенный класс функций), для которой числа точек разбиения t_i отрезка [a,b] минимально и 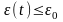, здесь – допустимое значение погрешности, – оценка отклонения x(t) от V(t) в соответствии с принятым критерием P(t) – приближенных.

Выбор типа базисных.

Выбор типа базисных функций в основном определяется требованиями ограничения сложности устройств дискретизации и восстановления сигнала. При восстановлении исходного сигнала совокупность выборок x(t) ставится в соответствии некоторый многочлен

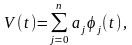
значения которого в точках отсчета t_i совпадает со значениями функции x(t).

Воспроизводящие функции V(t) обычно совпадают с приближающими, хотя в общем случае могут и отличаться от них.

Основные типы функций, применяемые в задачах дискретизации: ряд Фурье, ряд Котельникова, полиномы Чебышева, полиномы Лежандра, степенные полиномы, функции Уолта, функции Хаара, гипергеометрические.

4) Принцип приближения.

По принципу приближения можно выделить три группы методов:

– интерполяционные;

– экстраполяционные;

– комбинированные;

Экстраполяционные методы не требуют задержки сигнала при дискретизации т.е. они могут использоваться в управляющих системах, которые работают в реальном времени.

Интерполяционные обеспечивают меньшую избыточность отсчетов по сравнению с экстраполяционными методами, однако требуют задержки сигнала на интервал интерполяции.

При интерполяционно–эктраполяционных методах процедура нахождения приближающих функций p(t) разбивается на два этапа. На первом этапе методами интерполяции находится приближающая функция P(t) для начальной части . На втором этапе найденная функция экстраполируется для значений 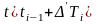и проверяется отклонение сигнала от этой функции.

При выборе шага дискретизации рассматриваются различные модели сигналов и вводятся соответствующие критерии отбора отсчетов.

1. Частотный критерий, при котором интервалы между отсчетами выбираются с учетом частотного спектра дискретизируемого сигнала;

2. Корреляционный критерий отсчетов, устанавливающий связь интервалов между отсчетами с интервалами корреляции сигнала;

3. Квантовый критерий отсчетов, предложенный для детерминированной модели сигнала и устанавливающий зависимость интервалов между отсчетами от значения ступени квантования по уровню и крутизны (первый производной) сигнала.