50. Эффективное кодирование (Методика Шеннона и Фэно, методика Хафмена)

В процессе кодирования, учитывая статистические свойства источника сообщений можно минимизировать среднее число двоичных символов, требующихся для выражения одной буквы сообщения, что при отсутствии шума позволяет уменьшить время передачи информации.

Такое эффективное кодирование базируется на основной теореме Шеннона (теорема №1) для каналов без шума: Сообщения Z, составленные из букв некоторого алфавита можно закодировать так, что среднее число двоичных символов на букву l_ср будет сколько угодно близко к энтропии источника этих сообщений Н(Z), но не меньше этой величины, т.е. l_ср=> Н(Z), но!: l_ср ≥ Н(Z).

Методика Шеннона –­ Фэно.

Для случая отсутствия статистической взаимосвязи между буквами конструктивные методы построения эффективных кодов даны впервые Шенноном и Фэно. Код Шеннона и Фэно строится следующим образом:

Z : Z₁,Z₂,…,Z_n – буквы;

p : p(Z₁), p(Z₂),…, p(Z_n) – вероятности.

P(Z_i) упорядочиваются по убыванию, множество Z делятся на две группы так, чтобы сумма вероятностей в каждой подгруппе были по возможности одинаковы. Всем буквам верхней половины в качестве первого символа приписывается 1, а всем нижним – 0. Каждая из полученных групп в свою очередь разбивается на две подгруппы с одинаковыми суммарными вероятностями и т.д.. Процесс повторяется до тех пор, пока в каждой подгруппе не останется по одной букве.

Пример 1.

Z	Z1	Z2	Z3	Z4	Z5	Z6	Z7	Z8
P(Z)	½	¼	1/8	1/16	1/32	1/64	1/128	1/128
Код	1	01	001	0001	00001	000001	0000001	00000001

Достигается наибольший эффект сжатия

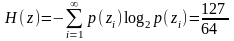
где n(z_i) – число символов кодовой комбинации, соответствующей знаку z_i.

Пример 2.

Z1	0,22	11
Z2	0,2	101
Z3	0,16	100
Z4	0,16	01
Z5	0,1	001
Z6	0,1	0001
Z7	0,04	00001
Z8	0,02	000001

H(z)=2.76

l_ср=2.84

Осталась некоторая избыточность, которая может быть устранена, если перейти к кодированию достаточно большими блоками.

Пример 3.

Сообщение состоит из двух знаков Z₁ и Z₂ с вероятностью появления P(Z₁)=0,9; P(Z₂)=0,1

При кодировании блоков, содержащих по две буквы, получим следующие коды

Z1 Z1	0,81	0
Z1 Z2	0,09	01
Z2 Z1	0,09	001
Z2 Z2	0,01	000
Блоки	Вероятности	Кодовые комбинации

(Так как знаки статистически не связаны, вероятности блоков определяется как произведение вероятностей составляющих знаков)

l_ср =1,29

l_ср/букву =0,645

Теоретически минимум может быть достигнут при кодировании блоков, включающих бесконечное число знаков.

Недостатки методики Шеннона–Фэно – неоднозначность. От этих недостатков избавлена методика Хаффмана.

Методика Хаффмана.

Методика Хаффмана гарантирует однозначное построение кода с наименьшим для данного распределения вероятностей средним числом символов на букву.

Для двоичного кода методика сводится к следующему: Буквы алфавита сообщений выписываются в основной столбец в порядке убывания вероятностей; Две последние буквы объединяются в одну вспомогательную букву, которой приписывают суммарную вероятность. Вероятности букв, не участвовавших в объединении и полученная суммарная вероятность снова располагаются в порядке убывания вероятностей в дополнительном столбце, а две последние объединяются. Процесс продолжается до тех пор, пока не получим единственную вспомогательную букву с вероятностью, равной единице.

Пример:

Знаки	Вероятности	1	2	3	4	5	6	7
z1 z2 z3 z4 z5 z6 z7 z8	0,22 0,20 0,16 0.16 0.10 0.10 0,04 0,02	0,22 0,20 0,16 0,16 0,10 0,10 0,06	0,22 0,20 0,16 0,16 0,16 0,10	0,26 0,22 0,20 0,16 0,16	0,32 0,26 0,22 0,20	0,42 0,32 0,26	0,58 0,42	1

Для составления кодовой комбинации соответствующей данному знаку необходимо проследить путь перехода знака по строкам и столбцам таблицы. Для наглядности строится кодовое дерево. Из точки, соответствующей вероятности 1 направляются две ветви, причем, ветви с большой вероятностью присваивается символ 1, а с меньшей 0. Такое последовательное ветвление продолжается до тех пор, пока не будет достигнута вероятность каждой буквы. Затем, двигаясь по кодовому дереву сверху вниз можно записать для каж­дой буквы соответствующую ей кодовую комбинацию:

z1 z2 z3 z4 z5 z6 z7 z8

01 00 111 110 100 1011 10101 10100

Построенные по указанным выше методикам коды с неравномерным распределением символов, имеющие минимальную среднюю длину кодового слова, называют оптимальными неравномерными кодами (ОНК).

Максимально эффективными будут те ОНК, у которых:

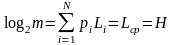
Эффективность ОНК оценивают при помощи коэффициента статистического сжатия:

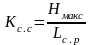(25)

и коэффициента относительной эффективности:

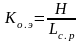(26)

Коды Шеннона–Фэно и Хаффмана удовлетворяют требованиям префиксности: ни одна комбинация кода не совпадает с началом более длинной комбинации.