37. Спектры периодического сигнала
Совокупность гармонических составляющих, образующих сигнал несинусоидальной формы называют спектром этого негармонического сигнала.
Спектр наглядно можно представить в виде спектральной диаграммы – так принято называть графическое изображение коэффициентов ряда Фурье для конкретного сигнала. Различают амплитудные и фазовые спектральные диаграммы. При этом по горизонтальной оси в некотором масштабе откладывают частоты гармоник, а по вертикальной оси представлены их амплитуды и начальные фазы.
Например, если некоторый периодический несинусоидальный сигнал описывается рядом
,
то его aмплитудную
спектральную диаграмму смотри на рисунке
6 а , а частотную – на рисунке 6 б.
Рисунок 6
38. Спектры непериодических сигналов
Непериодический сигнал легко получить из периодического, увеличивая период вплоть до Т ≥ ∞ . Спектры амплитуд для сигналов с разными периодами .
При увеличении периода сигнала частота первой гармоники ω1 = 2π/Т понижается. Спектральные линии становятся гуще. Амплитуды гармоник уменьшаются. Последнее становится понятным, если учесть, что энергия сигнала, оставаясь неизменной, перераспределяется теперь между возросшим числом гармоник. Естественно, доля каждой гармоники в общем сигнале падает.
Следовательно, при переходе к непериодическому сигналу (например, к одиночному импульсу) мы получаем в спектре такого сигнала вместо отдельных гармоник бесконечно большое число синусоидальных колебаний с бесконечно близкими частотами, заполняющими всю шкалу частот. Причем амплитуда каждого такого колебания становится исчезающе малой, потому что на его долю приходится бесконечно малая часть энергии сигнала. Другими словами, в любой бесконечно узкой полосе частот мы всегда обнаружим синусоидальное колебание, правда, бесконечно малой амплитуды.
Поскольку сравнивать между собой бесконечно малые величины неудобно, то вместо амплитуд Ак по оси ординат – откладывают произведение Ак Т, которое с увеличением периода Т остается постоянным. В новых координатах спектр. Понятие спектра амплитуд здесь лишено смысла и заменяется понятием спектральной плотности амплитуд, которая указывает, по сути, на удельный вес бесконечно малой амплитуды синусоидального колебания в любой бесконечно узкой полосе частот. Понятие спектра фаз заменяется понятием спектральной плотности фаз.Таким образом, спектр непериодического сигнала является в общем случае не дискретным, а непрерывным .
39. Распределение энергии в спектре
Пусть непериодический сигнал описывается функцией ƒ(t). Тогда энергию, выделяемую сигналом на сопротивлении в 1 ом, можно записать:
.
Предположим, что ƒ(t) абсолютно интегрируема (интеграл сходится). Выразим энергию W через модуль спектральной характеристики F(ω).
Квадрат модуля спектра амплитуд можно представить в виде http://peredacha-informacii.ru/ :
,
где F(–jω) – комплексно-сопряженная функция от спектральной характеристики F(jω).
;
.
Согласно определению можно записать:
.
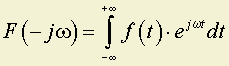Рассмотрим выражение:
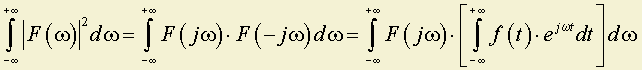
и поменяем очередность интегрирования
.
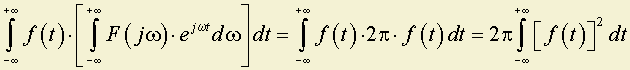Однако в соответствии с обратным преобразованием Фурье:
.
Или окончательно:
.
Оказывается, что энергия при интегрировании квадрата временной функции во временном интервале равняется энергии при интегрировании квадрата модуля спектра амплитуд по всему интервалу частот (теорема Парсеваля).