1. Векторлар жүйесінің рангы. Матрицалардың рангы туралы теоремалар

Сызықтық кеңістікте векторлар жүйесінің рангісі деп осы векторлар жүйесінің сызықты қабықшасының өлшемін атайды.

Теорема1. L сызықты кеңістіктің a=(a₁ …a_k) векторлар жүйесінің рангісі тең болады:

а) а векторлар жүйесіндегі сызықты тәуелсіз векторлардың максималды санына;

б) a₁ …a_k векторларының координаталарының бағандарынан құралған матрицаның рангісіне.

g – L кеңістігіндегі қайсыбір базис болсын. g базисіндегі a_i, векторларының координаталарының бағандарынан A матрицасын құрастырайық. a_i векторларына қолданылатын сызықты амалдар олардың координаталарының бағандарына қолданылады. Сол себепті, векторлар сызықты тәуелсіз болады, сонда және тек сонда ғана, егер олардың координаталарының бағандары сызықты тәуелсіз болса. Базисті минордың теоремасы бойынша А матрицасының рангісі оның сызықты тәуелсіз бағандарының максималды санына тең. Бұл а жүйесіндегі сызықты тәуелсіз векторлардың максималды санына сәйкес келеді. Демек, теореманың а) және б) пікірлері эквивалентті.

А матрицасында қайсыбір базисті минорды таңдайық және осы минордың бағандарын белгілейік. Оларға сәйкес келетін векторлар базисті деп аталады. Базисті минор туралы теоремада, біріншіден, базисті бағандар сызықты тәуелсіз және базисті векторлар сызықты тәуелсіз жүйені құрайды, екіншіден, матрицаның қалған бағандары базистердің сызықты комбинациялары болып табылады. Демек, а жүйесінің кез келген векторларының сызықты комбинациясы базисті векторлар жүйесінің сызықты комбинациясына сәйкестендіріледі.

Мысал. L төртөлшемді сызықты кеңістікте a₁, a₂, a₃, a₄ векторлары берілген, 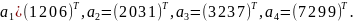Сәйкес А матрицасы келесідей түрде:

Матрицаның рангісін есептейміз, 2-ге тең. Сол себепті, векторлар жүйесінің рангісі 2-ге тең. Екінші ретті минор базис екенін оңай тексере аламыз. Сол себепті осы векторлар жүйесінің сызықты қабықшасының базисі жүйенің кез келген екі векторы болады. Мысалы, базис болып a₁, a₂ екі векторы болады. Сол себепті базисті ажыратуға болады. векторын базис бойынша ажырату үшін, келесі сызықты алгебралық теңдеуді шешу жеткілікті:

Координаталар түріндегі формасы:

Төрт теңдеуден кез келген екеуін қалдыруға болады. Екінші және үшінші теңдеуді қолданып, табамыз, .

Матрицалардың рангы.

А – өлшемдегі матрица, k – m және n-нан аспайтын натуралды сан: А матрицасының k-шы қатарының миноры деп, А матрицасының k-шы қатары мен k-шы бағанының қиылысуында тұрған элементтерден құралған k-шы ретті матрицаның анықтауышы.

Матрицаның рангісі деп базисті минордың реті аталады. Нөлдік матрицада базисті минор жоқ. Сол себепті нөлдік матрицасының рангісі нөлге тең. А матрицасының рангісі rg A деп аталады.

Мысал. Матрицаның барлық базисті минорлары мен рангісін табу керек.

Берілген матрицаның үшінші қатарындағы минорлары нөлге тең. Матрицаның алғашқы екі қатарында орналасқан екінші реттегі минор базис болып табылады. Нөлден өзгеше, мүмкін болатын алты минорды жинаймыз:

Осы бес минордың әр қайсысы базис болады. Матрицаның рангісі 2-ге тең.

Теорема. Матрицаның рангісі осы матрицаның сызықты тәуелсіз қатарларының максималды санына тең.

rg A = r болсын. Онда А матрицасында r сызықты тәуелсіз қатар бар. Бұл қатарларда базисті минор орналасқан. Егер де олар сызықты тәуелді болса, онда бұл минор нөлге тең болушы еді, ал матрицаның рангісі r-ге тең болмаушы еді. r – сызықты тәуелсіз қатарлардың максималды саны екенін, яғни кез келген p қатары p>r шартына тәуелді екенін көрсетейік. Осы p қатарлардан B матрицасын құрайық. B матрицасы – А матрицасының бір бөлігі, онда rg B ≤ rg A = r< p. Демек, B матрицасының ең болмағанда бір қатары бұл матрицаның базисті минорына кірмейді. Базисті минор туралы теоремаға сәйкес ол базисті минор орналасқан қатарлардың сызықты комбинациясына тең. Демек, B матрицасының қатарлары сызықты тәуелді.

Салдар 1. Матрицадағы сызықты тәуелсіз қатарлардың максималды саны сызықты тәуелсіз бағандардың максималды санына тең.

Салдар 2. Матрицаның қатарларын қарапайым түрде түрлендірген кезде, осы матрицаның бағандарының сызықты тәуелділігі сақталады.

А матрицасының кез келген k-шы бағандарын таңдап, олардан B матрицасын құрамыз. Егер B матрицасының бағандары сызықты тәуелсіз болса, онда k=rgB, онда матрицасының бағандары да сызықты тәуелсіз, k=rg . Егер B матрицасының бағандары сызықты тәуелді (k>rgB) болса, онда матрицасының бағандары сызықты тәуелді (k>rg ) болады. Демек, А матрицасының кез келген бағанының сызықты тәуелді немесе сызықты тәуелсіздігі қатарларды қарапайым түрлендіруде сақталады.