1. Комбинаторика элементтері. Жәшіктен шарлар таңдаудың әртүрлі схемалары.

n компонентті комбинация деп x= (x₁, x₂,…, x_n) деп түрінде ашылып жазылатын элементін айтады. x_i – бұл x комбинациясының i-нші компоненті деп аталады.

Т-ма(комбинаториканың негізгі ережесі) x= (x₁, x₂,…, x_n) n компонетті комбинациядан тұратын қандай да бір X жиыны берілген. Егер келесі шарт-р ор-са:

1) Бұл жиындағы барлық комбинация-да қарас-да, x₁ компоненті N₁ әр түрлі мәндер қабылдай алатын болса.

2) x₁ компоненті бекітілген барлық комб-ды бөлек қарас-да, олар-ң x₂ компонентасы N₂ әр түрлі мән қабылдай алатын болса ж/е N₂ саны x₁-дің барлық бекітулерінде бірдей болса.

3) x_1, x₂ компоненталары бекітілген барлық комб-ды бөлек қарас-да, олардың x₃ комп-сы N₃ әр түрлі мән қабылдай алатын болса ж/е N₃ саны x₁ мен x₂ –ң барлық бекітулерінде бірдей болса.

.......

n) x₁, x₂,…, x_n-1 x_n N_n N_n x₁, x₂,…, x_{n-1 .} Онда берілген X жиынында N₁ * N_{2 *} .... * N_n комб-я бар.

Қайталанымсыз комбинациялар. Бұл жағдайда бас жиынтықтан алынған элемент кері қайтарылмайды. Көлемі n-ге тең бас жиынтық алынған көлемі r-ге тең қайталанымсыз таңдамалардың сандарын табамыз.

2. Шартты ықтималдық. Ықтималдықтарды көбейту формуласы.

Сынақ жүргізу барысында қандай да бір А оқиғасының болуына В оқығасының болуы қалай әсер ететіні туралы сұрақ туындайды. Осы екі оқиғаның арасындағы байланысқа қарапайым м/лдар: В оқиғасының болуы А оқиғасының болуына міндетті түрде алып келеді н/е В оқиғасының болуы А оқиғасының болмауына алып келеді. Ықтималдықтар теориясында А ж/е В оқиғаларының арасындағы байланыс шартты ықтималдық ретінде сипатталады. Ол P(A|B) А оқиғасы В оқиғасы орындалған кезде:

P(A|B) = P(AB)/P(B) (1)

А-ма: - қандайда бір ықтималдық кеңістік . А,В – оқиғалар, .

В орындалады деп ұйғарғандағы А оқиғасының шартты ықтималдығы деп санын айтады ж/е оны деп белгілейді .

Шартты ықтималдық қарапайым ықтималдық қасиеттерінің бәріне ие:

• 

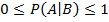
• Егер ,

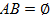• Егер ,

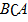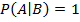
• Егер А қиылыспайтын А₁ , А₂ , А₃... оқиғалардың бірігуі болса,

онда

1-м/л. Қызыл ж/е қара түсті екі ойын сүйегі бір мезгілде лақтырылады.

а) түсетін ұпайлардың қосындысы 8 болу ықтималдығын табу керек

б) қызыл сүйекте жұп ұпай түседі деп есептеп, түсетін ұпайлардың қосындысы 8 болу ықтималдығын қайта есепте

Шешуі:

А) - қызылда , - қарада түскен ұпай , ,

Ықтималдықтың классикалық а-масын қолданамыз

б) , , , , , - В оқиғасы орындалады деп ұйғарғандағы А оқиғасының шартты ықтималдығы деп аталады

Мұндағы А оқиғасының а) пунктіндегі есептелген ықтималдығы шартсыз ықтималдық деп аталады, ал б) пунктіндегі есептелген ықтималдығы шартты ықтималдық деп аталады.

Ықтималдықтарды көбейту формуласы

(1)-ден

Сол сияқты

Бұл формулалар екі оқиға үшін ықтималдықты көбейту формулалары деп аталады. А,В,С- үш оқиға үшін ықтималдықты көбейту формулаласы

болады.

- оқиғалары үшін ықтималдықты көбейту формулаласы