10. Сандық қатарлар. Абсолют ж/е шартты жинақты қатарлар. Қатар жинақтылығының жеткілікті шарттары.

Сандық қатарлар. Абсолют ж/е шартты жинақты қатарлар.

Ан. , n өрнегі ақырсыз сандық қатард.а.. Ал сандары қатардың мүшелері, мұндағы - қатардың жалпы мүшесід.а..

Ан. Мына қосындыларды жазып алайық: Бұл қосындылар қатардың дербес қосындыларыд.а..

Ан. Егер қатардың n да S деребес қосыныдысының ақырлы шегі S бар болса, онда қатар жинақталатын қатар деп аталып, былай жазылады . S саны қатардың қосындысыд.а.. lim болса,қатар жинақты; lim , онда қатар жинақсыз.

Енді мүшелері комплекс сандар болатын

u +u +…= u (1) қатарын ж/е оның мүшелерінің абсолют шамаларынан құралған

| u |+|u |+…= |u | (2) қатарын қарастырайық. Егер (2) қатар жинақты болса, онда (1)қатар абсолют жинақты қатард.а.. Егер (1) қатар жинақты , ал (2) қатар жинақсыз болса, онда (1) қатар шартты жинақты қатард.а..

11. Функционалдық тізбек-р ж/е қатар-р. Функ-қ тізбек-р мен қатар-р бірқалыпты жинақтылығының жеткілікті белгілері.

Функционалдық тізбектер ж/е қатарлар.

Мүшелері нақты х айнымалысының функциясы Болатын қатарын функционалдық қатар дейді. функциялары анықталған ж/е қатары жинақты болатын х айнымалының мәндер жиыны функционалдық қатардың жинақталу облысы делінеді. Функционалдық қатардың жинақталу облысы Ох осінің қандай да бір аралығы болады. Алғашқы n мүшелерінің қосындысы болса, онда . Мұндағы берілген қатардың мүшелерінің қалдығыд.а..

Функционалдық тізбектер мен қатарлар бірқалыпты жинақтылығының жеткілікті белгілері.

Егер D облысында (2.3) қатардың барлық мүшелері шартты қанағаттандырса, мұндағы -тұрақты оң сандар, сонымен бірге (2.6) сандық қатар жинақты болса, берілген (2.3) қатар D облысында бір қалыпты (әрі абсолют) жинақты болады. Дәлелдеу.

қатары D облысының әрбір z нүктесінде жинақты, өйткені оның мүшелері жинақты (2.6) қатардың сәйкес мүшелерінен артық емес. Демек, берілген (2.3) қатар D облысының әрбір z нүктесінде абсолют жинақты болады. (2.3) қатардың қосындысы мен бірінші n мүшелерінің қосындысының сәйкес S(z) пен (z) белгілеп, мынаны аламыз: (2.7)

Шарт бойынша (2.4) қатар жинақты болатындықтан, оның қалдық мүшесі

қандай болмасын (ε>0) үшін жеткілікті үлкен n N = N=N(ε)-нан бастап ε-нан кем болады. Сөйтіп, (2.7) теңдіктен D облысындағы z нүктесіне тәуелсіз мынаны аламыз:

n <=N = N=N(ε) болғанда < ε.

Бұл (2.3) қатардың D облысында бірқалыпты жинақталатындығын дәлелдейді.

12. Дәрежелік қатар-р ж/е олардың жинақталу облысы. Дәр-к қатар-р мүшелеп инт-у ж/е мушелеп диф-у. Функ-ды дәрежелік қатарларға жіктеу.

түрінде берілген функциялық қатар дәрежелік қатард.а.. Егер болса, онда бұл қатар мына түрге көшеді. .

Егер (11.6) дәрежелік қатар болғанда жинақталатын қатар, ал болғанда жинақталмайтын қатар болса, онда саны дәрежелік қатардың жинақталу радиусы н/е жинақталу облысы деп аталады.

Жинақталу радиусын анықтау үшін келесі формулаларды қолданады ж/е . Мысал. дәрежелік қатардың жинақталу радиусы анықтау керек.

Шешімі: Мұнда , сон-тан .

Жинақталу интервалы .

Мысал. функциялық қатардың жинақталу радиусы табу керек.

Шешімі. Мұнда , онда . Жинақталу интервалы .

Жинақты интервалында дәрежелік қатарды Ɐ рет мүшелеп дифференциалдауға ж/е интегралдауға болады.

Дәрежелік x функциясының, мұндағы n– еркін алынған 1–ден артық натурал сан,туындысын есептеуге арналған формула мынадай: (x )'=nx (1.6)

Бұл ережелер дәлелдеулермен беріледі.Осы ережелерді қолдану арқылы функциялардың туындылары табылады. Дәрежелік қатардың қосындысыныңтуындысын дәрежелік қатарды мүшелеп дифференциалдау арқылы алуға

болады, яғни

,

,

,

,

Мүшелеп интегралдау әдіс: Мүшелеп интегралдау формуласы деп келесі теңдікті айтамыз.

(1)

Мүшелеп интегралдау формуласы бір интегралды екінші интеграл арқылы өрнектейді. Бұл формула екінші интегралды есептеу мүмкіндігі болған жағдайда қолданылады. Кей жағдайда соңғы нәтижені алу үшін бөліктеп интегралдау әдісін қайталап қолдануға тура келеді.

1) - түрдегі интеграл

Егер, -п-дәрежелі көпмүшелік болып, келесі , k=Const, функциялардың бірі болса, онда деп алып, бөліктеп интегралданады. Бұл жағдайда мүшелеп интегралдау п рет қайталанады.

2) -түріндегі интеграл

Егер -п дәрежелі көпмүшелік, ал -келесі функциялардың бірі болса

, онда . Деп алып, бөліктеп интегралданады.

3) түріндегі интегралдар, мұндағы , a,b- тұрақты сандар.

Бұл интегралдар айналымды интегралд.а. ж/е екі рет бөліктеп интегралдау арқылы алғашқы интегралы бар теңдеуге келеміз. Интеграл осы теңдеуді шешу арқылы есептеледі.

Мысал 1. интегралын есептеу керек.

Шешуі деп аламыз.

Сонда .

(1)-формуласы бойынша,

Соңғы интегралға да мүшелеп интегарлдау әдісін пайдаланып

теңдігіне келеміз. Интегралдың осы мәнін (2) теңдігіне қойып, берілген интегалды табамыз:

Соңында,

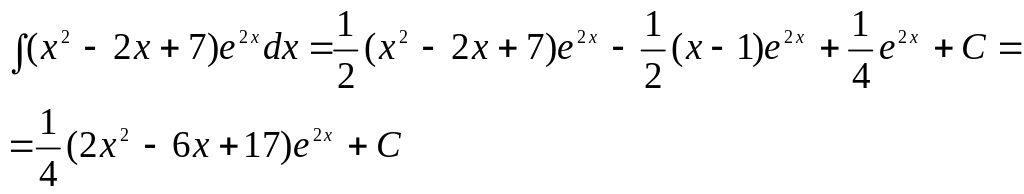
Функцияларды дәрежелік қатарларға жіктеу.

f (x) функциясы a -R <x <a +R аралығында анықталған ж/е Ɐ ретті туындылары бар болсын. Тейлор формуласы бойынша

мұндағы 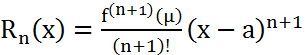, µ=a+ (x-a), Егер n , (x) 0 болса, онда

қатары Тейлор қатарыд.а.. (x) - Тейлор қатарының қалдық мүшесі дейді. Егер a =0 болса, онда Тейлор қатары Маклорен қатарыд.а. да

түрінде жазылады. Егер f (x) функциясы (a-R;a+R) аралығында анықталып, Ɐ n үшін теңсіздігі орындалса (мұндағы М-оң тұрақты сан), онда осы функция Тейлор қатарына жіктеледі. Кейбір функциялардың Маклорен қатарына жіктелуін көрсетейік:

1. ( )

2. ( )

3. ( )

4. ( )

5. ( )

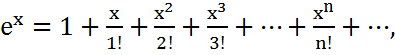Соңғы жіктеуде: болса, онда .

-1< болса, онда .

болса, онда .