6. Функция-ң интегралдануы-ң қажетті ж/е жеткілікті шарт-ры. Анықталған интеграл-ң орта мәні тур tHлар.

Функцияның интегралдануының қажетті ж/е жеткілікті шарттары. Айталық Х ж/е У нақты сандардан тұратын жиындар болсын.

1-Ан. Егер белгілі бір ереже (заң) бойынша Х жиынын құрастыратын әрбір нақты х санына у жиынын құрастыратын сандардың біреуі бірғана у сәйкес келсе, онда Х жиынында бір мәнді y=f(x) функциясы берілген дейді.Мұнда Х жиынын функцияның анықталу н/е берілу облысы, ал У жиынын функцияның мәндерінің облысы, х-ті тәуелсіз айнымалы н/е аргументі дейді.

Үздіксіз f(x) функциясы берілсін. Белгісіз функцияның туындысы -қа тең болсын,- яғни

(1) теңдікті қанағаттандыратын F(x) функцияны функцияның алғашқы функциясыд.а..

TH . Егер F(x) функциясы , функцияның алғашқы функциясы болса, онда F(х)+C да (С- тұрақты сан ) алғашқы функция болып табылады, ж/е керісінше, әрбір алғашқы функция F(х)+C түрде сипатталанады.

Туындының қасиеттері арқылы табамыз:

Айталық Ф(х) мына функция үшін кезкелген алғашқы функция болсын, онда

Сон-тан

Осы F(х)+C (С-тұрақты сан) өрнекті функцияның анықталмаған интегралыд.а. ж/е оны былай белгілейді

Мұндағы f(x)- интеграл астындағы функция, - интеграл астындағы өрнек. Алғашқы функцияны табу амалы f(x) функциясын интегралдауд.а.. Ендеше, интегралдау амалының дұрыс орындалғандығын тексеру үшін алғашқы функцияны дифференциалдап, интеграл астындағы функцияны алсақ болғаны.

Анықталған интегралдың орта мәні туралы THлар.

Анықталған интеграл түсінігі.

Ан. анықталған интегралы деп [a, b] аралығында f(x) функциясының алғашқы образының өсімшесін айтамыз:

Сонымен қатар, Ɐ f(x) функциясы үшін интегралы бар болады (а – Ɐ).

Орта мән туралы TH1.   y= f(x) функциясы   [a,b] кесіндісінде үзіліссіз болсын, онда бұл кесіндіден 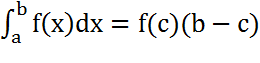 теңдігі орындалатындай  c нүктесі табылады.

Бұл   f(c) мәні функцияның    [a,b] аралығындағы орта мәнід.а..

Мысал: F(x)= [0,100]

│¹⁰⁰₀ =20/3

Орта мән туралы TH2

Th: _{[a,b] аралығында монотонды}

Д /уі g(x) [a,b] өспейтін болсын

( G(x)-g(b) ф-сы [a,b] де теріс емес өспейтін ж/е [a,b] да интегралданады.

Оған 2ши Лемманы қолдансақ

7. Бірінші ж/е екінші текті меншіксіз интеграл-р. Меншіксіз интег-ң жинақтылы-ң жеткілікті шарттары.

1. Бірінші жəне екінші текті меншіксіз интегралдар

I а) f функциясы [a,+∞) аралығында берілсін;

б) f - кез келген ақырлы [a b ′] , кесіндісінде мұндағы , b ′ ∈ ( a +∞) интегралданатын болсын. Eгер болса, онда ол шек f(x) функциясының [a, ∞] аралығындағы (бірінші текті) меншіксіз интегралыд.а. да келесі түрде белгіленеді

(1)

II. а) f шекті [a ,b) аралығында берілген жəне b- нүктесінің маңайында шектелмеген функция;

б) f кез келген [a, b ′] кесіндісінде (a < b ′ < b интегралданатын функция болсын. Егер (2) шегі болса, онда ол шек f функциясының [ a,b] кесіндісіндегі (екінші текті) меншіксіз интегралыд.а. да оны деп жазылады. (1) жəне (2) интегралдарды жинақтыд.а..

Егер f функциясы үшін І н/е ІІ шарттың тек бірі ғана орындалса, онда

деп жазылады да (1) ж/е (2) интегралдары жинақты д.а. f(x) функциясы ақырсыз аралығында анықталған ж/е Ɐ ақырлы кесіндісінде интегралданатын функция дейік. Егер шегі бар болса, онда ол шек аралығында f(x) функциясының меншіксіз интегралы д.а. да арқылы белгіленеді. Егер шек ақырлы болса, онда меншіксіз интеграл жинақталады дейді. Егер де бұл шек ақырсыз болса, н/е тіпті болмаса, онда интеграл жинақталмайтын меншіксіз интегралд.а.. Дәл осы сияқты жарты интервалда ж/е интервалда меншіксіз интегралды анықтауға болады, яғни .

Айталық F(x) берілген f(x) функциясының алғашқы функциясы болсын. Онда Ньютон-Лейбниц формуласы бойынша интегралдардың есептеу формулаларын келтіруге болады:

,

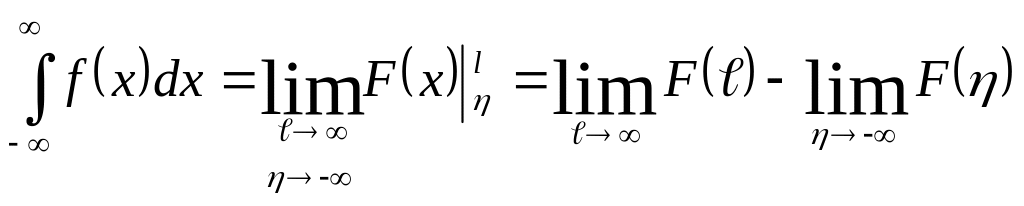
Мысалдар:1) меншіксіз интегралын жинақтылыққа зертелік.

Шешуі. Бірінші текті меншіксіз интегралды есептеудің (1) формуласы бойынша : 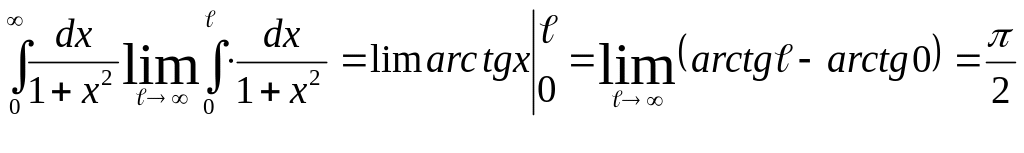Берілген меншіксіз интеграл –жинақты.