63

Разделы:

1 – Основные понятия технической термодинамики

2 – Первый закон термодинамики

3 – Термодинамические процессы

4 – Термодинамика водяного пара

5 – Второй закон термодинамики

6 – Термодинамика газового потока (термодинамика открытых систем)

7 – Механика жидкостей и газов (динамика идеальной жидкости)

8 – Механика жидкостей и газов (динамика реальной жидкости)

9 – Основы теории подобия

10 – Основные понятия теории тепло- и массообмена

11 – Конвективный теплообмен – в случае вынужденного движения

12 – Конвективный теплообмен при свободном движении

13 – Перенос тепла теплопроводностью

14 – Радиационный теплообмен

15 – Плавление металла

16 – Характеристики процесса нагрева металла

17 – Режимы нагрева металла

18 – Утилизация тепла – регенеративные теплообменники

19 – Утилизация тепла – рекуперативные теплообменники

20 – Теплообмен в слое кускового материала (шихта)

1 Термодинамической системой называется:

A) система, имеющая во всех своих частях одинаковый состав и физические свойства;

B) система, не взаимодействующая с окружающей средой;

C) совокупность макроскопических тел, обменивающихся энергией друг с другом и окружающей средой;

D) не допускает обмена с окружающей средой, как теплотой, так и работой;

Е) процесс, который можно осуществить в прямом и обратном направлениях через одни и те же промежуточные состояния без дополнительной затраты энергии.

2 Термодинамическая система называется изолированной, если она:

А) не допускает обмена с окружающей средой; как теплотой, так и работой;

В) по составу и физическому строению внутри не имеет поверхностей раздела (лед, вода, газы);

С) состоит из нескольких гомогенных частей (фаз) с различными физическими свойствами, отделенных одна от другой видимыми поверхностями раздела (лед и вода, вода и пар);

D) представляет совокупность макроскопических тел, обменивающихся энергией друг с другом и окружающей средой;

Е) имеет во всех своих частях одинаковый состав и физические свойства.

3 Термодинамическая система называется адиабатной (теплоизолированной), если она:

A) имеет во всех своих частях одинаковый состав и физические свойства;

B) по составу и физическому строению внутри не имеет поверхностей раздела (лед, вода, газы);

C) представляет совокупность макроскопических тел, обменивающихся энергией друг с другом и окружающей средой;

D) имеет адиабатную оболочку, которая исключает обмен теплотой (теплообмен) с окружающей средой;

Е) совершает процесс, который можно осуществить в прямом и обратном направлениях через одни и те же промежуточные состояния без дополнительной затраты энергии.

4 Термодинамическая система называется однородной, если она:

A) представляет совокупность макроскопических тел, обменивающихся энергией друг с другом и окружающей средой;

B) имеет адиабатную оболочку, которая исключает обмен теплотой (теплообмен) с окружающей средой;

C) имеет во всех своих частях одинаковый состав и физические свойства;

D) состоит из нескольких гомогенных частей (фаз) с различными физическими свойствами, отделенных одна от другой видимыми поверхностями раздела (лед и вода, вода и пар);

Е) не допускает обмена с окружающей средой, как теплотой, так и работой.

5 Система называется гомогенной, если она:

A) имеет во всех своих частях одинаковый состав и физические свойства;

B) однородная по составу и физическому строению, внутри нее нет поверхностей раздела (лед, вода, газы);

С) представляет совокупность макроскопических тел, обменивающихся энергией друг с другом и окружающей средой;

D) имеет адиабатную оболочку, которая исключает обмен теплотой (теплообмен) с окружающей средой;

Е) не допускает обмена с окружающей средой, как теплотой, так и работой.

6 Система называется гетерогенной, если она:

A) представляет совокупность макроскопических тел, обменивающихся энергией друг с другом и окружающей средой;

B) имеет адиабатную оболочку, которая исключает обмен теплотой (теплообмен) с окружающей средой;

C) имеет во всех своих частях одинаковый состав и физические свойства;

D) не допускает обмена с окружающей средой, как теплотой, так и работой;

E) состоит из нескольких гомогенных частей (фаз) с различными физическими свойствами, отделенных одна от другой видимыми поверхностями раздела (лед и вода, вода и пар).

7 В тепловых машинах (двигателях) механическая работа совершается с помощью рабочих тел – газ, пар. Рабочее тело – это:

A) такой газ, у которого отсутствуют силы взаимного притяжения и отталкивания между молекулами;

B) тело, посредством которого производится взаимное превращение теплоты и работы (в паровых турбинах – водяной пар, в газовых турбинах – газ ...);

С) это характеристика конкретных условий, в которых находится данная система;

D) параметры, не зависящие от массы системы;

Е) параметры, значения которых пропорциональны массе системы.

8 Основные термодинамические параметры состояния (также называют термическими параметрами) следующие:

A абсолютное давление, абсолютная температура, удельный объем;

B давление, удельный объем, удельная теплоемкость;

C удельная энергия, удельная теплоемкость;

D удельные скрытые теплоты фазовых переходов;

E избыточное давление, изобарная теплоемкость.

9 Основные термодинамические параметры состояния (также называют калорическими параметрами) следующие:

А давление, удельный объем, удельная теплоемкость;

В температура, объем;

С внутренняя энергия, энтальпия, энтропия, теплоемкость;

D избыточное давление;

E внутренняя энергия.

10 Термическими коэффициентами, характеризующими тепловые и упругие свойства тел, называются:

А изотермический коэффициент сжимаемости γ, коэффициент динамической вязкости μ;

В коэффициент объемного расширения α, коэффициент кинематической вязкости ν;

С термический коэффициент давления β, коэффициент скорости φ;

D коэффициент объемного расширения α, термический коэффициент давления β, изотермический коэффициент сжимаемости γ;

E коэффициент объемного расширения α, ускорение свободного падения g.

11 Какое состояние тела называется равновесным состоянием?

А уравнение состояния как для идеальных, как и для реальных газов, описывается тремя параметрами по уравнению f (Р, υ, Т) = 0;

B состояние тела, при котором во всех его точках объема давление Р, удельный объем υ и температура Т и все другие физические свойства одинаковы;

C совокупность изменений состояния термодинамической системы при переходе из одного состояния в другое;

D состояние тела, при котором значения основных параметров термодинамической системы пропорциональны массе системы (объем, энергия, энтропия и т.д.);

E состояние тела, при котором основные параметры термодинамической системы связаны между собой уравнением f (Р, υ, Т) = 0.

12 В термодинамике полная энергия макросистемы равна , где Е_КИН – кинетическая энергия системы; Е_ПОТ – потенциальная энергия системы во внешних силовых полях; U – внутренняя энергия. Чем определяется изменение внутренней энергии ∆U?

A определяется значениями энергии в конечном и начальном состояниях системы, т.е. ;

B определяется как сумма внутренних энергий составляющих частей этой системы;

C изменение внутренней энергии ∆U определяется формой пути процесса;

D определяется величиной работы, совершаемой над системой при перемещении ее из одного места силового поля в другое;

E определяется уравнением .

13 Термодинамический процесс – это:

А) процесс изменения состояния рабочего тела во времени;

В) процесс, при протекании которого в каждый момент времени и во всех точках объема рабочего тела одноименные параметры р и Т имеют одинаковое значение;

С) процесс, который можно осуществить в прямом и обратном направлениях через одни и те же промежуточные состояния без дополнительной затраты энергии;

D) процесс, когда обязательным условием обратимости для процессов сжатия и расширения является отсутствие трения;

Е) процесс, в котором условием обратимости для процессов передачи тепла от одного тела к другому является равенство температур тел, обменивающихся теплом.

14 Термодинамический процесс называется равновесным, если:

A) термодинамическая система не взаимодействует с окружающей средой;

B) значения параметров пропорциональны массе системы;

C) процесс можно осуществить в прямом и обратном направлениях через одни и те же промежуточные состояния без дополнительной затраты энергии;

D) параметры не зависят от массы системы;

E) при протекании процесса в каждый момент времени и во всех точках объема рабочего тела одноименные параметры р и Т имеют одинаковое значение.

15 Равновесным состоянием тела называется состояние, при котором:

А) параметры не зависят от массы системы;

В) во всех точках объема р, ν и Т и все другие физические свойства одинаковы;

С) изменение внутренней энергии ∆U определяется как сумма внутренних энергий составляющих частей этой системы;

D) значения параметров пропорциональны массе системы;

Е) основные параметры термодинамической системы связаны между собой уравнением f (Р, υ, Т) = 0.

16 Уравнение состояния идеального газа, записанное для т кг газа, имеет вид:

А ;

В ;

С ;

D ;

E .

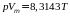17 Уравнение состояния реальных газов имеет вид:

A ;

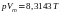B ;

C ;

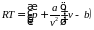D ;

E .

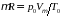18 Первый закон (НАЧАЛО) термодинамики является частным случаем всеобщего закона сохранения энергии М.В. Ломоносова. Первая математическая форма записи уравнения первого закона термодинамики имеет следующий вид:

А ;

В ;

C ;

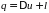D ;

E .

19 Вторая математическая форма записи уравнения первого закона термодинамики имеет следующий вид:

А ;

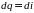В ;

С ;

D ;

E .

20 В уравнении первого закона термодинамики в правой части записаны следующие составляющие:

A du – изменение внутренней энергии, dl – изменение внешней энергии;

B du – элементарное изменение внешней энергии газа; dl – элементарное количество теплоты;

C du – элементарное изменение внутренней энергии газа, dl – элементарное количество работы, совершенной газом;

D du –элементарное количество теплоты, dl – элементарное количество работы, совершенной газом;

E du – элементарное количество работы, совершенной газом; dl – элементарная механическая работа.

21 В уравнении первого закона термодинамики в правой части записаны следующие составляющие:

A di – полная энергия единицы массы газа, dl₀ – располагаемая работа;

B di – сумма внутренней энергии и потенциальной энергии давления, dl₀ – элементарная механическая работа;

C di – элементарное изменение энтальпии, dl₀ – располагаемая работа;

D di – элементарное количество теплоты, dl₀ – элементарное количество работы, совершенной газом;

E di – количество теплоты, поглощенное системой, dl₀ – располагаемая работа для m кг массы газа.

22 Функциями состояния рабочего тела являются:

А давление, удельная теплоемкость;

В внутренняя энергия, энтальпия и энтропия;

C удельные скрытые теплоты фазовых переходов;

D удельная энергия, температура;

E избыточное давление.

23 Теплоемкость газа зависит от его температуры. По этому признаку различают среднюю и истинную теплоемкость. Каким уравнением представляют нелинейную зависимость истинной теплоемкости от температуры?

A ;

B ;

C ;

D , где a, b , d – величины, постоянные для данного газа;

E .

24 В зависимости от количества вещества, к которому подводится теплота, теплоемкость различают:

A изохорная теплоемкость с_v, удельная мольная теп­лоемкость с_μ;

B изобарная теплоемкость с_р, удельная объемная теплоемкость с′;

C удельная массовая теплоемкость с_х, изохорная теплоемкость с_v;

D изобарная теплоемкость с_р, истинная теплоемкость С;

E удельная массовая теплоемкость с_х [Дж/(кг·К)], удельная объемная теплоемкость с′ [Дж/м³·К)], удельная мольная теп­лоемкость с_μ [Дж/(моль· К)].

25 Как определяется удельная теплоемкость смеси, если смесь газов задана массовыми долями:

A , ;

B , ;

C , ;

D , ;

E , .

26 Массовые теплоемкости при постоянных давлении и объеме связаны между собой уравнением:

А ;

В [кДж/(кг·К)];

C ;

D ;

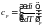E .

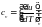27 Изохорная теплоемкость имеет обозначение:

А) с′_р В) µс_v ; С) с_mр ; D) µс_р ; Е) с_р

28 Изобарная теплоемкость имеет обозначение:

А) µс_v ; В) с_mv; С) с′_mv; D) µс_р ; E) с′_v .

29 Действительный процесс перехода из жидкого в газообразное состояние изображается изобарой АВ на pv-диаграмме. Для реального вещества в pv-диаграмме область двухфазного состояния (влажного пара):

A расположена левее кривой АК;

B расположена правее ВК;

C расположена между кривыми АК и ВК;

D расположена правее ВК и выше точки К;

E расположена ниже СК.

30 При каких условиях, исходя из pv-диаграммы на рисунке, можно превращать газы в жидкое состояние:

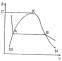
A сжимать газ увеличивая давление;

B при температурах выше критической по изотерме, имеющей монотонно спадающий характер;

C сжимать газ по изобаре СК;

D газ охладить до температуры ниже критической, затем сжимать по изотерме;

E при абсолютной температуре кипения, когда исчезает различие между жидким и парообразным состоянием вещества.

31 Изменение состояния рабочего тела может осуществляться различными способами, среди которых выделяют четыре основных процесса. Термодинамический процесс, происходящий при постоянном объеме, называется:

A изобарным;

B изотермическим;

C адиабатным;

D изохорным;

E политропным.

32 Соотношение между основными параметрами рабочего тела (р и Т) в начале и в конце изохорного процесса следующее:

А ;

В ;

С ;

D ;

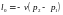E .

33 Количество подведенной (или отведенной) удельной теплоты q_v в изохорном процессе графически определяется:

A площадью под кривой процесса в координатах T-s;

B площадью под кривой процесса в координатах p-v;

C подкасательной кривой изохорного процесса в T-s-координатах;

D проекцией кривой процесса на горизонтальную ось в p-v-координатах;

E проекцией кривой процесса на вертикальную ось в p-v-координатах.

34 Из уравнения первого закона термодинамики для изохорного процесса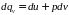 (v = const или dv = 0) следует, что:

А вся подводимая (отводимая) к рабочему телу теплота идет на совершение внешней работы;

В работа в изохорном процессе равна нулю, вся подводимая (отводимая) к рабочему телу теплота идет на изменение внутренней энергии;

C для двухатомного газа 28,5% подведенной к рабочему телу теплоты идет на совершение внешней работы, а 71,5% - на изменение внутренней энергии;

D работа изменения объема, располагаемая работа в процессе и удельное количество теплоты равны между собой;

E теплота, подведенная к рабочему телу, идет на изменение энтальпии.

35 Соотношение между основными параметрами рабочего тела (v и T) в начале и в конце изобарного процесса следующее:

A ;

B ;

C ;

D ;

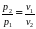E .

36 Из уравнения первого закона термодинамики для изобарного процесса следует что:

A часть теплоты, подведенной к рабочему телу, идет на изменение внутренней энергии, а оставшаяся часть идет на совершение работы;

B вся подводимая (отводимая) к рабочему телу теплота идет на совершение внешней работы;

C работа в изобарном процессе равна нулю, вся подводимая (отводимая) к рабочему телу теплота идет на изменение внутренней энергии;

D теплота, подведенная к рабочему телу, идет на изменение энтропии;

E теплота, подведенная к рабочему телу, идет на изменение энтальпии.

37 Соотношение между основными параметрами рабочего тела (р и v) в начале и в конце изотермического процесса следующее:

А ;

В ;

С ;

D ;

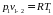E .

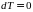38 Уравнение изотермического процесса имеет вид:

A ;

B ;

C ;

D ;

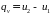E .

39 Из уравнения первого закона термодинамики для изотермического процесса при dТ = 0 следует:

A вся теплота, подводимая к рабочему телу, идет на совершение работы, изменение внутренней энергии равно нулю;

B вся теплота, подводимая к рабочему телу, идет на изменение внутренней энергии, работа равна нулю;

C работа изменения объема, располагаемая работа в процессе и удельное количество теплоты не равны между собой;

D теплоемкость в изотермическом процессе имеет постоянное значение;

E часть теплоты, подведенной к рабочему телу, идет на изменение внутренней энергии, а оставшаяся часть идет на совершение работы.

40 Как называется процесс, протекающий без теплообмена с окружающей средой?

A изобарным;

B изотермическим;

C адиабатным; D изохорным; E политропным.

41 Уравнение адиабатного процесса имеет вид:

A ;

B ;

C ;

D ;

E .

42 Из уравнения первого закона термодинамики для адиабатного процесса (dq = 0) следует, что:

A в адиабатном процессе работа совершается за счет убыли внутренней энергии;

B работа изменения объема, располагаемая работа в процессе и удельное количество теплоты не равны между собой;

C вся теплота, подводимая к рабочему телу, идет на совершение работы, изменение внутренней энергии равно нулю;

D теплота, подведенная к рабочему телу, идет на изменение энтропии;

E теплота, подведенная к рабочему телу, идет на изменение энтальпии.

43 Как называются процессы, в которых, при определенных условиях, происходит изменение всех термодинамических параметров?

A изобарные;

B политропные;

C изотермические;

D адиабатные;

E изохорные.

44 Уравнение политропного процесса имеет вид:

А ;

В ;

С ;

D ;

E .

45 При каких условиях политропные процессы переходят в изохорный, изобарный, изотермический и адиабатный?

A при n = 1;

B когда в формуле , в диапазоне изменения показателя политропы 1<n<k, теплоемкость оказывается отрицательной;

C когда в формуле , в диапазоне изменения показателя политропы 1<n<k, теплоемкость оказывается положительной;

D когда п принимает определенные значения от -∞ до +∞;

E при n = 0.

46 Насыщенный пар – это:

А пар в процессе превращения вещества из жидкого состояния в газообразное;

В пар, находящийся в равновесном состоянии с жидкостью, из которой он получается;

C пар в процессе перехода вещества из газообразного состояния в жидкое;

D пар в процессе превращения вещества из жидкого состояния в газообразное с увеличением температуры;

E пар в процессе превращения вещества из жидкого состояния в газообразное с изменением температуры и давления среды.

47 Сухой насыщенный пар – это:

A пар, находящийся в равновесном состоянии с жидкостью, из которой он получается;

B пар в процессе перехода вещества из газообразного состояния в жидкое;

C пар в процессе превращения вещества из жидкого состояния в газообразное с увеличением температуры;

D пар, который не содержит частиц жидкой фазы; его состояние определяется одним параметром – давлением или температурой;

E пар в процессе превращения вещества из жидкого состояния в газообразное с изменением температуры и давления среды.

48 Влажный насыщенный пар – это:

A пар, который содержит мельчайшие капельки жидкости;

B пар, который не содержит частиц жидкой фазы; его состояние определяется давлением;

C пар, который содержит частицы жидкой фазы; его состояние определяется температурой;

D пар в процессе превращения вещества из жидкого состояния в газообразное при постоянной температуре;

E пар в процессе превращения вещества из жидкого состояния в газообразное при постоянном давлении.

49 Степень сухости пара (или паросодержание) – это:

A отношение общей массы (пар + жидкость) влажного насыщенного пара (т_с + т_Ж) к массе сухого насыщенного пара т_с, содержащегося во влажном паре

;

B массовая доля жидкости во влажном паре, обозначается (1 – х);

C отношение массы (пар – жидкость) влажного насыщенного пара т_с – т_Ж к массе сухого насыщенного пара т_с, содержащегося во влажном паре

;

D отношение массы жидкости, из которой образуется влажный насыщенный пар т_Ж к массе сухого насыщенного пара т_с, содержащегося во влажном паре

;

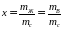E отношение массы сухого насыщенного пара т_с, содержащегося во влажном паре, к общей массе (пар + жидкость) влажного насыщенного пара т_с + т_Ж

;

50 Чему равна степень сухости х сухого насыщенного пара?

A х = 1; B х = 0; C х = 0,5; D х = 0,1; E х = 0,75.

51 Массовая доля жидкости во влажном паре называется:

A степенью влажности пара и обозначается (1 – х);

B степенью сухости х влажного насыщенного пара;

C степенью перегрева влажного пара и обозначается (х +1);

D независимым параметром процесса кипения жидкости;

E функцией состояния влажного пара.

52 Степень перегрева пара – это:

A температура образования влажного насыщенного пара;

B разность между температурой t_П перегретого пара и температурой t_S сухого насыщенного пара;

C разность между температурой сухого насыщенного пара и влажного насыщенного пара;

D это температура получения сухого насыщенного пара;

E разность плотностей сухого насыщенного пара и влажного насыщенного пара.

53 На pv-диаграмме для воды (рисунок) что представляет собой термодинамическая система между точками b и c, как она называется?

A смесь кипящей воды с насыщенным паром – влажный насыщенный пар;

B отрезок bc представляет собой изобару и изотерму одновременно;

C здесь свойства воды и насыщенного пара неразличимы;

D представляет сухой насыщенный пар, точка на верхней пограничной кривой;

E геометрическое место точек, соответствующих началу кипения.

54 На pv-диаграмме для воды (рисунок) что представляет собой термодинамическая система в точке с?

A геометрическое место точек, соответствующих началу кипения;

B смесь кипящей воды с насыщенным паром – влажный насыщенный пар;

C здесь свойства воды и насыщенного пара неразличимы;

D вся вода превращается в пар, система в точке с представляет сухой насыщенный пар;

E соответствует воде при температуре 0 ⁰С.

55 На pv-диаграмме для воды (рисунок) что представляет собой термодинамическая система в точке d?

A перегретый пар;

B точка, в которой все свойства воды и насыщенного пара неразличимы;

C смесь кипящей воды с насыщенным паром;

D система в точке представляет сухой насыщенный пар;

E точка, соответствующая началу кипения.

56 На pv-диаграмме для воды (рисунок) что представляет собой термодинамическая система в точке b?

A перегретый пар;

B точка, в которой все свойства воды и насыщенного пара неразличимы;

C система в точке представляет сухой насыщенный пар;

D смесь кипящей воды с насыщенным паром;

E система представляет собой воду при температуре насыщения (кипения) T_s.

57 На pv-диаграмме для воды (рисунок) показать чему равна работа расширения от объема υ' до объема υ".

A соответствует длине отрезка bc;

B равняется проекции кривой Кb на ось ординат;

C соответствует пло­щади, расположенной между отрезком bc и осью абсцисс;

D соответствует проекции кривой Кс на ось абсцисс;

E равна отношению участков bc/bn.

58 На T-s-диаграмме для воды (рисунок) показать чему равна теплота, необхо­димая для полного превращения 1 кг воды в сухой насыщенный пар при температуре насыщения, т. е. скры­тая теплота парообразования r (Дж/кг)?

A соответствует площади между отрезком bc и осью абсцисс;

B соответствует длине отрезка bc;

C равняется проекции кривой Кb на ось ординат;

D соответствует проекции кривой Кс на ось абсцисс;

E равна отношению участков bc/bn.

59 Как называется кривая Кb на T-s-диаграмме для воды (рисунок) и чему равна степень сухости пара на этой кривой?

A верхняя пограничная кривая, х = 1;

B изотерма, х = 0,5;

C кривая сухости пара, х = 0;

D нижняя пограничная кривая, или кривая начала кипения, х = 0;

E политропа, степень сухости х = 0,3.

60 Как называется кривая Кс на T-s-диаграмме для воды (рисунок) и чему равна степень сухости пара на этой кривой?

A нижняя пограничная кривая, х = 0;

B изотерма, х = 0,5;

C верхняя пограничная кривая, х = 1;

D кривая сухости пара, х = 0;

E адиабата, степень сухости х = 0,3.

61 Первый закон термодинамики утвержда­ет, что возможен процесс, при котором система получает из окружающей среды энергию в форме теплоты, а возвращает в среду энергию в форме механической работы. Однако I закон не го­ворит о том, при каких условиях это преобразование возможно. Это устанавливает второй закон термодинамики, который позволяет:

А указать направление теплового потока и устанавливает максимально возможный предел превращения теплоты в работу в тепловых машинах;

В отметить, что все реальные состояния газа и процессы – неравновесные и необратимые;

C отметить, что необратимость учитывается эмпирическими коэффициентами;

D отметить, что равновесное состояние – состояние, при котором во всех точках объема давление, температура, удельный объем и физические свойства газа одинаковы;

E отметить, что если к газу подвести теплоту, то она пойдет на изменение внутренней энергии и работу против внешних сил.

62 Условия, необходимые для работы тепловой машины, следующие:

A к рабочему телу должна быть подведена энергия в виде внешней работы, которая превращается в теплоту и передается окружающей среде;

B работа расширения должна быть обязательно больше работы сжатия;

C теплота, подводимая от источника тепла q₁, должна быть больше теплоты q₂, передаваемой холодильнику;

D машина должна быть машиной периодического действия с чередованием в рабочем цикле процессов расширения с подводом теплоты и сжатия с отводом теплоты;

E в основе работы должны быть круговые термодинамические процессы.

63 Что называется термодинамическим циклом или круговым процессом?

A совокупность термодинамических процессов, возвращающих систему в первоначальное состояние;

B процессы, совершающиеся без теплообмена с окружающей средой;

C процессы, совершающиеся при постоянной температуре;

D процессы, протекающие по адиабате;

E процессы, изображенные в Ts-диаграмме.

64 Цикл на pv-диаграмме состоит из процесса расширения рабочего тела 1-2, происходящего в результате подвода теплоты q₁, и процесса сжатия 2-1 с отводом теплоты в количестве q₂. Чему равна работа расширения (графически), совершаемая газом?

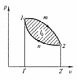
А площадь между кривыми 1-m-2-n-1;

В площадь между кривой 1-т-2 и осью абсцисс;

C площадь 1-n-2-2´-1´;

D площадь 1-m-2-n-1;

E проекция кривой 1-n-2 на ось абсцисс.

65 На Ts- диаграмме процесс расширения 1-2 – теплота q₁ подводится к рабочему телу; процесс сжатия 2-1 – теплота q₂ отводится от рабочего тела. Чему равна теплота (графически), полезно преобразованная в работу?

A площадь 2-2´-1´-1-n-2;

B проекция кривой 1-m-2 на ось абсцисс;

C площадь 1-m-2-n-1;

D площадь 1-m-2-2´-1´-1;

E проекция кривой 2-n-1 на ось абсцисс.

66 На pv-диаграмме обратный круговой процесс: процесс 1-2 – расширение, теплота q₂ отбирается от холодного источника тепла и передается рабочему телу; процесс 2-1 – сжатие, теплота q₁ отдается горячему источнику тепла. Чему равна совершаемая работа (графически) и какой у нее знак (положительная или отрицательная)?

А площадь 2-2´-1´-1-n-2, знак «плюс»;

В площадь 1-m-2-n-1, знак «минус»;

C проекция кривой 1-m-2 на ось абсцисс, знак «минус»;

D площадь 1-m-2-2´-1´-1, знак «плюс»;

E проекция кривой 2-n-1 на ось абсцисс, знак «плюс».

67 На pv-диаграмме приведен обратимый цикл Карно. Записать формулу термодинамического коэффициента цикла 1) через теплоту q₁ и q₂ и 2) через температуры Т₁ и Т₂.

А 1) , 2) ;

В 1) , 2) ;

C 1) , 2) ;

D 1) , 2) ;

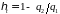E 1) , 2) .

68 Идеальный цикл теплового двигателя – цикл Карно, на практике неосуществим, так как:

А неосуществимы вообще обратимые процессы;

В состоит из двух изотермических и двух адиабатных процессов;

С принципиально невозможно проведение адиабатных процессов;

D термодинамический к.п.д. обратимого цикла Карно больше, чем к.п.д необратимого цикла;

E термодинамический к.п.д. цикла Карно не зависит от природы газа и определяется температурами источников тепла.

69 Способ повышения термодинамического к.п.д. реальных круговых процессов, широко используемый в практике, следующий:

A это рекуперативный цикл Карно, состоящий из двух изотермических процессов и двух политропных процессов расширения и сжатия;

B в систему тепловой машины включают теплообменник для отбора теплоты;

C адиабатные процессы в цикле Карно заменяют политропными с одним и тем же показателем политропы;

D направление всех процессов в цикле Карно должно быть обратным направлению в рассматриваемой в тепловой машине;

E в обратном цикле Карно работа сжатия больше работы расширения на определенную величину.

70 В основе работы холодильной установки лежит обратный круговой процесс: чем большее количество теплоты q₂ отбирается у охлаждаемого тела и чем меньше затрачивается на этот процесс внешняя работа l₀, тем совершеннее такая установка. Записать формулу коэффициента, которым характеризуют совершенство работы холодильных установок.

A холодильный коэффициент ;

B холодильный коэффициент ;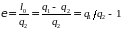

C термодинамический к.п.д. ;

D термодинамический к.п.д. ;

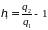E термодинамический к.п.д. .

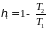71 Энтропией называется функция S состояния системы, дифференциал которой в элементарном обратимом процессе равен: . Чему равно абсолютное значение энтропии?

A энтропия тела может быть определена только с точностью до постоянного слагаемого S₀ (константы интегрирования):

;

B энтропия физически однородной системы является функцией двух независимых параметров состояния р и Т или T и V:

;

C энтропия физически однородной системы является функцией двух независимых параметров состояния р и Т или T и V:

;

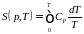D значение энтропии в необратимом теплообмене возрастает из-за необратимости процесса;

E при равенстве абсолютных температур источников теплоты энтропия имеет максимальное значение.

72 Один из аспектов понятия энтропии: энтропия – это мера потери работоспособности системы вследствие необратимости реальных процессов. Потеря работы от необратимости процесса прямо пропорциональна возрастанию энтропии. Это можно оценить количественно.

Например, изменение энтропии в обратимом процессе, протекающем в изолированной системе, равно нулю. Изменение энтропии для необратимого процесса имеет определенное значение и, соответственно, работа в результате необратимого процесса:

A уменьшается пропорционально возрастанию энтропии при постоянной температуре нижнего источника теплоты ;

В превращается в теплоту;

С останется без изменения;

D равна нулю при Т₁ = Т₂;

Е возрастает пропорционально возрастанию энтропии при постоянной температуре нижнего источника теплоты .

73 Для обычных термодинамических систем внутренняя энергия U неограниченно возрастает при Т →∞, поэтому абсолютная температура в равновесных состояниях может быть только положительной. Как ведет себя энтропия dS при нагревании тела и охлаждении?

A при нагревании dS>0, охлаждении dS<0;

B при нагревании dS<0, охлаждении dS>0;

C при нагревании dS=0, охлаждении dS<0;

D при нагревании dS>0, охлаждении dS=0;

E при нагревании и охлаждении не изменяется.

74 Единица измерения энтропии: 1) для 1 кг массы; 2) для любого количества вещества:

А 1) s, Вт/(м²·К), 2) S, Вт/К;

В 1) s, Дж/(кг·К), 2) S, Дж/К;

C 1) s, Вт/(м·К), 2) S, кВт/К;

D 1) s, Дж/(м³·К), 2) S, кДж/м²·К;

E 1) s, кДж/(кг·с²), 2) S, Дж/с·К.

75 Общая математическая формулировка второго закона термодинамики имеет вид:

A ;

B ;

C ;

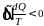D ;

E .

76 Уравнение первого закона термодинамики для газового потока при отсутствии сил тяжести и сил трения в газе, когда газ совершает лишь работу расширения и не производит полезной технической работы, имеет вид:

A , где – приращение кинетической энергии газа на выделенном участке;

B ;

C , где ρ – плотность газа в сечении; F – площадь поперечного сечения канала; w – скорость потока в сечении;

D , где – элементарная техническая работа;

E .

77 В тепловом двигателе механическая энергия потока получается в процессе его расширения. Первый закон термодинамики для потока для такой системы как тепловой двигатель, имеет вид:

A , т.е. работа теплового двигателя производится за счет уменьшения энтальпии газа;

B , где – приращение кинетической энергии газа на выделенном участке;

C ;

D ;

E .

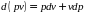78 Какие каналы называют соплами?

А каналы, в которых происходит повышение давления dp>0;

В каналы, в которых течение газа сопровождается его сжатием с увеличением давления dp>0;

С каналы, в которых происходит снижение давления газа dp<0 и увеличение скорости;

D каналы, в которых течение газа сопровождается его сжатием с увеличением давления и уменьшением скорости dw<0;

E каналы, в которых сечение остается неизменным.

79 Какие каналы называют диффузорами?

А каналы, в которых происходит снижение давления газа dp<0 и увеличение скорости;

В каналы, в которых сечение остается неизменным;

С каналы, в которых течение газа сопровождается его сжатием с увеличением давления dp>0 и уменьшением скорости dw<0;

D каналы, в которых происходит снижение давления газа dp<0 и снижение скорости;

E каналы, в которых давление и скорости газа будут постоянными dp = 0, dw = 0.

80 Стационарное течение газа описывается системой уравнений, включающей:

A уравнение неразрывности потока, уравнение состояния и уравнение 1-го закона термодинамики для потока;

B уравнение Навье-Стокса, уравнение состояния и уравнение 2-го закона термодинамики;

C неразрывности потока, уравнение Рихмана-Ньютона и уравнение энергии;

D уравнение Эйлера для статики, уравнение состояния и уравнение энергии;

E неразрывности потока, уравнение Бернулли и уравнение энергии.

81 Уравнение неразрывности газового потока имеет вид , или 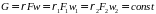, где G – массовый секундный расход газа; F₁, F₂ – площади поперечных сечений канала; w₁, w₂ – скорости в соответствующих сечениях; ρ₁, ρ₂ – плотности газа для тех же сечений потока (ρ = 1/ν), и характеризует:

A изменение скорости w по координате х;

B ускорение элементарной массы газа по координате х;

C изменение плотности потока между соответствующими сечениями;

D неизменность массового расхода газа в любом сечении канала при установившемся течении;

E скорость одномерного потока между соответствующими сечениями.

82 Скорость истечения w₂ из сопла может быть найдена путем интегрирования формулы для располагаемой работы l₀:

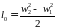. В случае, когда w₂>>w₁, величиной w₁ можно пренебречь и скорость на выходе сопла будет равна .

Как будет вести себя расход газа G и чему он будет равен при достижении w₂ значения, равного значению местной скорости звука а?

А увеличивается при w₂=а с понижением давления р₂;

В остается неизменным и равным максимальному G_max;

C равен расходу во входном сечении;

D уменьшается при w₂=а с понижением давления р₂;

E уменьшается при w₂=а с увеличением давления р₁.

83 При истечении идеального газа из сопла какая скорость называется критической скоростью истечения и как она обозначается?

А скорость w₂, равная местной скорости звука а, обозначается w_{2 КР};

B скорость w₁, обозначается w _КР;

C скорость , обозначается w₀;

D скорость , обозначается w;

E , обозначается w_СР.

84 Какое давление называют критическим р_КР при истечении идеального газа из сопла?

А давление р₁, соответствующее максимальному расходу газа G_max в сечении 1, называется р_1КР;

В давление р₂, соответствующее достижению максимального расхода газа G_max , называется р_2КР;

C давление р₂, равное (р₁)/2, называется р_2КР;

D давление р₂, равное 2р₁, называется р_2КР;

E давление р₁, равное (р₂)/2, называется р_1КР.

85 1) Какое отношение давлений при истечении идеального газа из сопла называется критическим. 2) От чего зависит критическое отношение давлений при истечении идеального газа из сопла?

А 1) отношение , обеспечивающее постоянный расход газа в сечениях 1 и 2; 2) от площади входного сечения F₁;

В 1) отношение 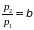, сохраняющее постоянным расход газа в сечении 2; 2) от отношения площадей сечений F₁/F₂;

С 1) отношение , обеспечивающее максимальный расход газа; 2) только от свойств газа (от показателя адиабаты k);

D 1) отношение , обеспечивающее минимальный расход газа при постоянной скорости истечения w₂; 2) от отношения скоростей в сечениях w₁/w₂;

E 1) отношение 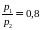, обеспечивающее максимальный расход газа; 2) от величины местной скорости звука а в сечении 2.

86 Какое сопло позволяет получить скорость истечения газа больше скорости звука, и чему равна длина суживающейся части этого сопла?

А конфузор; вычисляется по соответствующей формуле;

В диффузор; рассчитывается из заданного расхода газа;

С комбинированное сопло Лаваля; принимается равной диаметру минимального сечения;

D сужающееся сопло; рассчитывается из массового расхода идеального газа при минимальной площади сечения;

E расширяющееся сопло; рассчитывается из скорости истечения при минимальной площади сечения.

87 Как рассчитывается скорость истечения реального газа по формуле ?

A с помощью уравнения неразрывности потока;

B с помощью is-диаграммы;

C из первого закона термодинамики, записанного через энтальпию;

D из определения энтальпии;

E из уравнения для кинетической энергии при истечении газа из сопла.

88 Какой процесс называют 1) адиабатным дросселированием и 2) где на практике он имеет место. 3) Записать уравнение дросселирования для потока газа, если сечения канала до и после расширения одинаковы (рисунок).

А 1) процесс выравнивания давления между соответствующими сечениями канала; 2) течение жидкости или газа в трубах; 3) уравнение w₁ = w₂/2;

B 1) процесс падения давления жидкости или газа в сечении на выходе из трубы; 2) течение жидкости или газа в трубах;3) уравнение w₁ = 2w₂;

C 1) увеличение давления жидкости или газа в выходном сечении трубы; 2) течение жидкости или газа в трубах; 3) уравнение ;

D 1) необратимый переход рабочего тела от высокого давления р₁ к низкому давлению р₂ без теплообмена; 2) имеет место при прохождении жидкости или газа через вентили, задвижки и измерительные диафрагмы; 3) уравнение i₁ = i₂;

E 1) увеличение давления жидкости или газа при изменении направления движения потока в канале; 2) течение жидкости или газа в трубах; 3) уравнение .

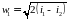89 1) В чем суть эффекта Джоуля-Томсона. 2) Какое состояние реального газа называется точкой инверсии.

A 1) в изменении температуры рабочего газа при дросселировании; 2) когда дроссельный эффект равен нулю, в этой точке происходит смена знака температурного эффекта;

B 1) изменение давления потока газа при дросселировании; 2) при β_КР, температура газового потока постоянная;

C 1) увеличение давления в потоке газа при течении в канале; 2) при w_КР, когда скорость равна местной скорости звука;

D 1) повышение скорости потока газа во входном сечении сопла; 2) когда ;

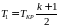E 1) уменьшение массового расхода газа при истечении из отверстия; 2) состояние, при котором .

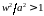90 Вид уравнения для работы теплового двигателя аналогичен уравнению для компрессора , где h₁ и h₂ – энтальпия газа на входе и выходе. Графически работа изображается аналогично как для теплового двигателя, так и для компрессора (рисунок).

В чем отличие процесса, происходящего в тепловом двигателе, от процесса, протекающего в компрессоре?

A в компрессоре процесс сжатия происходит от точки 2 к точке 1, а работа является затраченной, т.е. со знаком «минус» (- l_ТЕХ); в тепловом двигателе – наоборот;

B в тепловом двигателе расширение происходит от точки 2 к точке 1, работа отрицательная;

C в тепловом двигателе работа сжатия происходи от точки 1 к точке 2, работа положительная;

D отличие отсутствует;

E отличие в свойствах рабочего тела, т.е. показателя адиабаты k.

91 Жидкость, при движении которой отсутствуют силы внутреннего трения, называется:

A идеальной, или невязкой жидкостью;

B реальной жидкостью;

C жидкостью с постоянной вязкостью;

D жидкостью при одномерном движении;

E жидкостью с ламинарным режимом движения.

92 Одна из форм записи уравнения неразрывности для сжимаемой жидкости имеет вид (закон сохранения массы, записанный для единицы объема и для единицы времени), где представляет собой:

A разность между массой жидкости вышедшей из единичного объема в единицу времени, и массой жидкости поступившей в этот объем за то же время;

B массу жидкости единичного объема;

C изменение массы жидкости в контрольном объеме;

D изменение плотности в объеме во времени;

E изменение массы в единичном объеме за единицу времени.

93 Одна из форм записи уравнения неразрывности для сжимаемой жидкости имеет вид (закон сохранения массы, записанный для единицы объема и для единицы времени), где представляет собой:

А изменение массы в единичном объеме за единицу времени;

В разность между массой жидкости вышедшей из единичного объема в единицу времени, и массой жидкости поступившей в этот объем за то же время;

С изменение массы, содержащейся в единичном объеме, за единицу времени;

D массу жидкости единичного объема;

E изменение массы жидкости в контрольном объеме.

94 Имеется стационарное течение сжимаемой жидкости по трубе, сечение которой изменяется по длине. Пусть – среднее по сечению трубы значение плотности пото­ка массы, кг/м²·с, определяемое как интеграл: .

Что представляет собой интеграл от плотности потока массы по площа­ди поперечного сечения трубы?

A массовый рас­ход, т. е. массу жидкости, проходящую через поперечное сечение за единицу времени;

B изменение массы, содержащейся в единичном объеме, за единицу времени;

C среднее по сечению трубы значение плотности пото­ка массы;

D разность между массой жидкости вышедшей из единичного объема в единицу времени, и массой жидкости поступившей в этот объем за то же время;

E изменение плотности жидкости во времени.

95 Для стационарного течения сжимаемой жидкости по непроницаемой трубе интеграл от плотности потока массы по площади S = S(x) поперечного сечения трубы можно записать как выражение , где – массовый расход жидкости через поперечное сечение за единицу времени. Что представляет собой это выражение?

A уравнение не­разрывности для стационарного потока сжимаемой жидкости в трубе переменного сечения;

B изменение массы, содержащейся в единичном объеме, за единицу времени;

C среднее по сечению трубы значение плотности пото­ка массы;

D разность между массой жидкости вышедшей из единичного объема в единицу времени, и массой жидкости поступившей в этот объем за то же время;

E изменение плотности жидкости во времени.

96 Для стационарного течения несжимаемой жидкости можно записать выражение , где – среднее по сечению значение скорости; V – расход жидкости через поперечное сечение трубы S, м³/с. Что представляет собой это выражение?

А массовый рас­ход, т. е. массу жидкости, проходящую через поперечное сечение за единицу времени;

В изменение массы, содержащейся в единичном объеме, за единицу времени;

С уравнение не­разрывности для стационарного потока несжимаемой жидкости в трубе переменного сечения;

D среднее по сечению трубы значение плотности пото­ка массы;

Е разность между массой жидкости вышедшей из единичного объема в единицу времени, и массой жидкости поступившей в этот объем за то же время.

97 Силы, действующие в движущейся идеальной жидкости:

A сила тока, электромагнитная индукция;

B коэффициент поверхностного натяжения, силы притяжения между молекулами;

C градиенты концентраций в системе тел; коэффициенты переноса;

D внешние массовые силы, сила давления, силы инерции;

E градиент температуры, термические коэффициенты.

98 Уравнение движения идеальной жидкости в векторной форме (уравнение Эйлера) записывается в виде: . Что представляют собой слагаемые в правой части уравнения?

A – массовая плотность внешней массовой силы, – массовая плот­ность силы давления;

B - объемный расход жидкости; - градиент температуры;

C - коэффициент пропорциональности; - расход жидкости в единицу времени;

D - коэффициент пропорциональности; - вектор плотности потока жидкости;

E - объемный расход жидкости; - вектор плотности потока жидкости.

99 Зависит ли форма уравнения Эйлера от того, является ли жид­кость сжимаемой или несжимаемой?

A зависит, появляется слагаемое от изменения вязкости в потоке;

B зависит, так как появляются потери на трение в потоке;

C зависит, так как деформация объема в сжимаемой жидкости добавляет слагаемое в правой части уравнения;

D не зависит, так как сжатие или расширение идеальной жидкости, в связи с отсутствием вязкости, не приводит к появлению каких-либо новых сил;

E зависит, в левой части появляется слагаемое от изменения вязкости в потоке.

100 Трубкой тока (рисунок) называется поверхность, образованная всеми линиями тока, проходящими через замкнутый плоский кон­тур, ограничивающий площадь бесконечно малого размера dS (рисунок). 1) Что представляет собой линия тока? 2) Почему при стационарном движении жидкость движется вдоль трубки тока и нигде ее не пересекает (рисунок)?

A 1) представляет осевую линию трубки тока; 2) при стационарном движении частицы жидкости движутся между сечениями трубки;

B 1) линия тока представляет собой векторную линию скорости, т. е. геометрическое место точек, в которых вектор ско­рости направлен по касательной к этой линии; 2) при стационарном движении линия тока совпадает с траекторией ча­стицы жидкости;

C 1) представляет проекцию вектора скорости на ось у; 2) при стационарном движении частицы жидкости движутся по направлению, полученному во входном сечении трубки;

D 1) линия тока совпадает с направлением оси х для трубки тока; 2) при стационарном движении частицы жидкости входное и выходное сечения трубки тока находятся на одной оси;

E 1) представляет собой замкнутый контур в выходном сечении трубки; 2) при стационарном движении отсутствует закручивающий поток для частицы жидкости.

101 Аналитическое решение уравнений Эйлера для стационарного движения несжимаемой идеальной жидкости в трубке тока носит название:

A интеграл Эйлера;

B уравнения Навье-Стокса;

C уравнение Ньютона;

D уравнение Бернулли;

E уравнение Ньютона-Рихмана.

102 Уравнение Бернул­ли для трубки тока идеальной жидкости записывается в виде 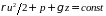, размерность Дж/м³ = Н/м² = Па.

Что представляет собой первое слагаемое ?

A имеет смысл объем­ной плотности потенциальной энергии давления и называется статическим давлением;

B представ­ляет собой объемную плотность потенциальной энергии по­ложения, называется геометрическим давлением;

C представляет собой объемную плот­ность кинетической энергии движущейся жидкости и называется динамическим давлением;

D статический напор;

E геометрический напор.

103 Уравнение Бернул­ли для трубки тока идеальной жидкости записывается в виде , размерность Дж/м³ = Н/м² = Па.

Что представляет собой второе слагаемое р?

A имеет смысл объем­ной плотности потенциальной энергии давления и называется статическим давлением;

B представляет собой объемную плот­ность кинетической энергии движущейся жидкости и называется динамическим давлением;

C представ­ляет собой объемную плотность потенциальной энергии по­ложения, называется геометрическим давлением;

D динамический напор;

E геометрический напор.

104 Уравнение Бернул­ли для трубки тока идеальной жидкости записывается в виде , размерность Дж/м³ = Н/м² = Па.

Что представляет собой третье слагаемое ?

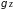А представляет собой объемную плот­ность кинетической энергии движущейся жидкости и называется динамическим давлением;

В имеет смысл объем­ной плотности потенциальной энергии давления и называется статическим давлением;

C динамический напор;

D статический напор;

E представ­ляет собой объемную плотность потенциальной энергии по­ложения, называется геометрическим давлением.

105 Уравнение Бернулли записывают в форме: , размерность – в метрах. Как называется каждое из слагаемых в уравнении?

A – статический напор; р/γ – скоростной напор; z – геометрический напор;

B – средняя скорость в сечении потока; р/γ – плотность жидкости в потоке; z – линейный размер сечения;

C – динамический напор; р/γ – статический напор; z – геометрический напор.

D – закон распределения скорости в сечении потока; р/γ – высота сечения потока от нулевой точки отсчета; z – размер сечения потока;

E – максимальное значение скорости течения; р/γ – ускорение течения потока; z – расстояние от уровня отсчета до средины сечения потока.

106 Движение реальной жид­кости может осуществляться в двух принципиально различных ре­жимах. Назовите эти режимы.

A ламинарный и турбулентный;

B вязкостный и пограничный;

C переходный и пограничный;

D переходный и конвективный;

E смешанный и гравитационный.

107 Уравнение Бернулли для потока реальной жидкости в трубе или канале имеет вид

,

где α₁, α₂ – коэффициенты Кориолиса. Что представляет собой слагаемое ?

A местное повышение давления в потоке;

B перепад давления между расчетными сечениями в потоке;

C характеристика трубопровода или канала;

D потери энергии потока в единицах давления;

E параметр жидкости для конкретного трубопровода или канала.

108 Потери энергии (или давления) при движении реальной жид­кости в трубах и каналах принято разделять на:

A стандартные потери, учитываемые задаваемым коэффициентом;

B потери давления на трение и на местные сопротивления и выражать как сумму этих двух видов потерь р_ПОТ. = р_ТР + р_М.С.;

C потери, регламентируемые для данной жидкости и данного трубопровода;

D не учитываемые и регламентируемые;

E потери, принимаемые в зависимости от условий движения жидкости.

109 Когда возникают потери на трение р_ТР при движении жидкости в каналах или трубопроводах и как определяются?

A при движении жидкости по прямоли­нейным участкам трубопроводов при отсутствии изменений по­перечного сечения трубы, определяются , где ξ_тр - коэффициент сопротивления трения;

B при движении жидкости по трубопроводу с изменением по­перечного сечения трубы, определяются коэффициентом ξ = (1 – S₁/S₂)², где S₁, S₂ - сечения трубопровода;

C при движении жидкости по трубопроводу с изменяемым направлением трубопровода, определяется по формуле 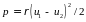, где u₁, u₂ – скорость в сечениях;

D потери на трение р_ТР возникают в неподвижной жидкости в каналах или трубопроводах, определяются коэффициентом , где L – длина исследуемого участка трубы, d_г - гидравлический диаметр трубы, λ – гид­равлический коэффициент трения, определяется по разному для двух различных режимов движения жидкости;

E при движении жидкости по трубопроводу в турбулентном режиме, определяется по формуле , где u_1,2 – скорость в сечениях.

110 Вы­ражение для коэффициента сопротивления трения имеет вид

, где:

A L – длина исследуемого участка трубы, d_г – периметр сечения трубы, λ коэффициент теплопроводности;

B L – рабочая длина трубы, d_г – эквивалентный диаметр трубы, λ – коэффициент трения для турбулентного режима;

C L – периметр поперечного сечения трубы, d_г – внутренний диаметр трубы, λ – коэффициент теплопроводности трубы;

D L – расчётная длина участка трубопровода, d_г – периметр сечения трубы, λ – гид­равлический коэффициент трения;

E L – длина исследуемого участка трубы, d_г – гидравлический диаметр трубы, λ – гид­равлический коэффициент трения, определяется по разному для двух различных режимов движения жидкости.

111 Величина потери давления на местные сопротивления определяется по формуле , где

A ξ_М.С - коэффициент пропорциональности, постоянная величина в зависимости от вида жидкости;

B ξ_М.С - коэффициент формы сечения трубы;

C ξ_М.С – постоянная величина, определяется режимом движения жидкости;

D ξ_М.С – коэффициент местного сопротивления, в большинстве случаев коэффициент находится экспериментально;

E ξ_М.С – коэффициент падения скорости по сечению потока.

112 В соответствии с тео­ремой Борда, потеря давления при вне­запном расширении (рисунок) равна динамическому давлению потерянной скорости .

Записать формулу для коэффициента местного сопротивления, если потеря давления рассчитывается:

1) по динамическому давлению в узком сече­нии;

2) по динамическому давле­нию в широком сечении.

A 1) 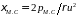, 2) ;

B 1) ξ_M.C = (1 – S₁/S₂)², 2) ξ_M.C = (S₂/S₁ –1)²;

C 1) ; 2) ;

D 1) ξ_M.C = (S₂/S₁ –1)²; 2) ;

E 1) ξ_M.C = (1 – S₁/S₂)², 2) .

113 Формула Ньютона для определения касательного напряжения трения, возникающего в потоке жидко­сти, движущемся в направлении оси х при наличии изменения скорости в направлении оси у имеет вид: .

Как называется коэффициент пропорциональности μ и его единицы измерения?

A кинематический коэффициент вязкости (м²/с);

B динамический коэффициентом вязко­сти, измеряется в (Па·с), физический параметр жидкости;

C коэффициент скорости, (м²/с);

D гидравлический коэффициент трения (м²/с);

E молярная масса (кг/моль).

114 Формула Ньютона для определения касательного напряжения трения, возникающего в потоке жидко­сти, движущемся в направлении оси х при наличии изменения скорости в направлении оси у может быть записана в виде: .

Как называется коэффициент пропорциональности ν и его единицы измерения?

A динамический коэффициентом вязко­сти, измеряется в (Па·с), физический параметр жидкости;

B коэффициент скорости, (м²/с);

C гидравлический коэффициент трения (м²/с);

D кинематический коэффициентом вязко­сти, измеряется в (м²/с), физический параметр жидкости;

E молярная масса (кг/моль).

115 Физический смысл кинематического коэффициента вязкости ν (м²/с).

А представляет собой ускорение протекающего в потоке жидкости процесса;

В характеризует статичность протекающего в потоке процесса;

С представляет собой коэффициент молекулярного переноса им­пульса и определяет интенсивность этого процесса;

D характеризует химические свойства текущей среды в потоке;

E характеризует стабильность параметров процесса в потоке.

116 Уравнение движения реальной жидкости в векторной форме (уравнение Навье-Стокса) имеет вид .

В чем отличие этого уравнения от уравнения Эйлера для идеальной жидкости?

А отличие отсутствует, уравнения аналогичны;

В в правой части присутствует вектор массовой плотности силы внутреннего трения;

C присутствует слагаемое гравитационной природы;

D добавлено слагаемое в правой части от действия электромагнитного поля;

E присутствует слагаемое от взаимного действия гравитации и электромагнитного поля.

117 Уравнение движения сжимаемой жидкости в векторной форме (уравнение Навье-Стокса) имеет вид .

Что представляет собой последнее слагаемое в правой части уравнения?

А уравнение неразрывности для реальной жидкости;

В сила внутреннего трения, обусловленная сжатием или расширением жидкости;

C гравитационная составляющая поля;

D ускорение свободного падения элемента потока;

E представляет собой силу от действия турбулентности в потоке.

118 Точное аналитическое решение уравнения Навье-Стокса получено для стационарного ламинарного течения жидкости в канале, образованном двумя бес­конечными плоскими пластинами, и трубе круглого сечения. Точное решение уравнений Навье-Стокса дает формулу для гидравлического коэффициента трения.

Записать формулу для определения коэффициента λ для 1) плоского канала, 2) трубы круглого сечения.

А 1) λ = Pr/Re, 2) λ = Pe/Re;

В 1) λ = 0,8/Re, 2) λ = 1/Re;

С 1) λ = 96/Re, 2) λ = 64/Re;

D 1) λ = Nu/Re, 2) λ = Bi/Re;

E 1) λ = Ar/Re, 2) λ = Gr/Re.

119 При расчете потерь давления на трение, прежде всего, определяют режим движения жидкости в трубе (рассчитывают число Рейнольдса). Если величина Рейнольдса меньше 2300, то:

1) какой режим движения;

2) по какой формуле определяют гидравлический коэффициент трения?

А 1) режим движения в гидравлически гладкой трубе, 2) формула Блазиуса;

В 1) режим движения в шероховатой трубе, 2) формула Никурадзе;

С 1) ламинарный, 2) λ = 64/Re;

D 1) переходный режим, 2) λ = 0,8/Re;

E 1) ламинарный, 2) формула Никурадзе.

120 При расчете потерь давления на трение прежде всего определяют режим движения жидкости в трубе. Если режим турбулентный, то:

1) какую роль играет шероховатость трубы;

2) по какой формуле определяют гидравлический коэффициент трения λ?

А 1) влияние шероховатости отсутствует, 2); в соответствии с эмпирической формулой Блазиуса;

В 1) абсолютная шероховатость стенки трубы меньше толщины ламинарного подслоя, имеем течение в гидравлически гладкой трубе; 2) при увеличении числа Рейнольдса гидравлический коэффициент трения уменьшается;

С 1) определяют – труба является гидравлически гладкой или шероховатой (из сравнения толщины ламинарного подслоя с абсолютной шероховатостью), 2) если абсолютная шероховатость больше толщины ламинарного подслоя, то λ не зависит от Рейнольдса – течение в шероховатых трубах; расчет λ по различным формулам. Например формула Никурадзе;

D 1) влияние шероховатости слабо сказывается на изменение коэффициента трения, 2) данные для определения гидравлического коэффициента трения приводятся в справочниках для различных случаев;

E 1) при увеличении числа Рейнольдса уменьшается толщина ламинарного подслоя, режим движения может быть как течение в гидравлически гладкой, так и гидравлически шероховатой трубе; 2) коэффициент λ определяется по формуле Блазиуса.

121 В формулу критерия Нуссельта 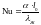входят значения:

A α – коэффициент температуропроводности, ℓ₀ – определяющий размер, λ_Ж – коэффициент теплоотдачи;

B α – коэффициент теплоотдачи, ℓ₀ – определяющий размер, λ_Ж - коэффициент динамической вязкости;

C α – коэффициент теплоотдачи, ℓ₀ – определяющий размер, λ_Ж – коэффициент теплопроводности жидкости;

D α – коэффициент теплопроводности, ℓ₀ – характерный размер, λ_Ж – коэффициент теплоотдачи;

E α – коэффициент кинематической вязкости, ℓ₀ – определяющий размер, λ_Ж – коэффициент теплопроводности жидкости.

122 Критерий Нуссельта характеризует:

A физические свойства жидкости;

B стационарную теплоотдачу при вынужденной конвекции.

C соотношение между силами инерции и силами трения в потоке жидкости;

D стационарную теплоотдачу при свободной конвекции несжимаемой жидкости;

E соотношение между силами инерции и силами тяжести в потоке жидкости.

123 Критерий Рейнольдса : 1)характеризует; 2) в формулу входят значения:

A 1) неустановившееся движение жидкости; 2) w₀ – скорость жидкости вдали от обтекаемого тела, ℓ₀ – характерный линейный размер, ν – динамическая вязкость жидкости;

B 1) соотношение между силами инерции и силами тяжести в потоке жидкости; 2) w₀ – угловая скорость жидкости, ℓ₀ – характерный линейный размер, ν – кинематическая вязкость жидкости;

C 1) физические свойства жидкости; 2) w₀ – средняя скорость жидкости в сечении, ℓ₀ – коэффициент динамической вязкости, ν – кинематическая вязкость жидкости;

D 1) стационарную теплоотдачу при свободной конвекции; 2) w₀ – динамическая вязкость жидкости, ℓ₀ – определяющий линейный размер, ν – линейная скорость жидкости;

E 1) соотношение между силами инерции и силами трения в потоке жидкости; 2) w₀ – характерная для данной задачи скорость жидкости, ℓ₀ – характерный линейный размер, ν – кинематическая вязкость жидкости.

124 В формулу критерия Прандтля входят значения:

A ν – коэффициент кинематической вязкости, а – коэффициент температуропроводности;

B ν – коэффициент динамической вязкости, а – коэффициент теплоотдачи;

C ν – коэффициент кинематической вязкости, а – коэффициент теплопроводности;

D ν – скорость жидкости в рассматриваемой точке, а – характерный линейный размер;

E ν – коэффициент динамической вязкости, а – коэффициент теплоотдачи.

125 Критерий Прандтля характеризует:

A соотношение между силами инерции и силами трения в потоке жидкости;

B соотношение между силами инерции и силами тяжести в потоке жидкости;

C химические свойства жидкости;

D физические свойства жидкости;

E стационарную теплоотдачу при вынужденной конвекции.

126 Критерий Грасгофа 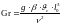: 1)характеризует; 2) в формулу входят значения:

A 1) подъемную силу, возникающую в жидкости вследствие разности плотностей; 2) β – термодинамический коэффициент расширяемости, 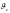- температурный напор, g – ускорение силы тяжести, ℓ - характерный размер, ν – кинематическая вязкость;

B 1) соотношение между силами инерции и силами трения в потоке жидкости; 2) β – термический коэффициент давления, - температурный напор, g – ускорение силы тяжести, ℓ - характерный размер, ν – динамическая вязкость;

C 1) стационарную теплоотдачу при свободной конвекции несжимаемой жидкости; 2) β – изотермический коэффициент сжимаемости, - безразмерная температура, g – ускорение силы тяжести, ℓ - характерный размер, ν – кинематическая вязкость;

D 1) стационарную теплоотдачу при вынужденной конвекции; 2) β – термический коэффициент давления, - температурный напор, g – ускорение силы тяжести, ℓ - определяющий размер, ν – удельный объем;

E 1) физические свойства жидкости; 2) β – коэффициент объемного расширения, - линейная скорость, g – ускорение силы тяжести, ℓ - характерный размер, ν – кинематическая вязкость.