МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ
Запорізький національний технічний університет
Індивідуальні ЗАВДАННЯ
з вищої математики
для студентів технічних спеціальностей
денної форми навчання
( 2-й семестр)
111 частина
2011
Укладачі: Розділи „Теорія поля”, „Теорія стійкості”- В.Г. Засовенко, доцент, к.ф.-м. н., А.В. Засовенко, ст. викл., к.т.н.
Розділ „ Диференціальні рівняння” - І.М. Килимник, доцент, к.т.н., Л.І. Паталаха , ас., Т.Г. Полякова, ас.
Рецензент: В.М. Онуфрієнко, проф., к.ф.-м. н.
Відповідальний за випуск: - І.М. Килимник, доцент, к.т.н.
Затверджено
на засіданні кафедри
„Вищої математики”
Протокол № 7 від 24 березня 2011 р
Зміст
|
|
Стор. |
1. |
Теорія поля |
4 |
1.1 |
Аудиторне заняття |
4 |
1.2 |
Варіанти індивідуальних завдань |
5 |
2. |
Диференціальні рівняння |
14 |
2.1 |
Диференціальні рівняння 1-го порядку |
14 |
2.1.1 |
Аудиторне заняття |
14 |
2.1.2 |
Індивідуальні завдання |
17 |
2.2 |
Диференціальні рівняння вищих порядків та системи диференціальних рівнянь |
37 |
2.2.1 |
Аудиторне заняття |
37 |
2.2.2 |
Індивідуальні завдання |
41 |
3. |
Теорія стійкості |
73 |
3.1 |
Аудиторне заняття |
73 |
3.2 |
Варіанти індивідуальних завдань |
74 |
|
Література |
86 |
1. Теорія поля
Аудиторне заняття.
Скалярне поле визначене функцією
.
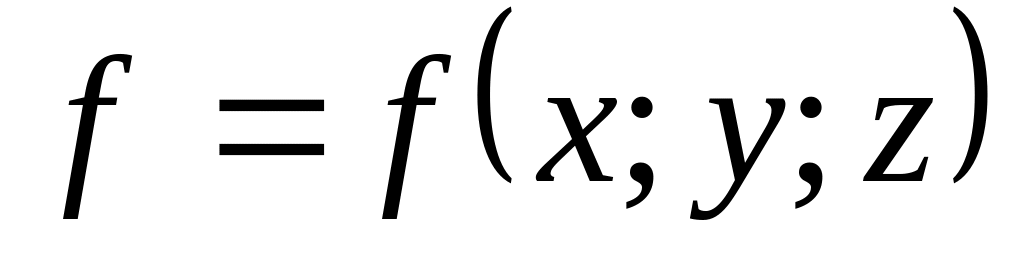Знайти його градієнт та побудувати
поверхню рівня
.
.
Відповідь:
,
гіперболічний параболоїд.
Знайти значення похідної функції
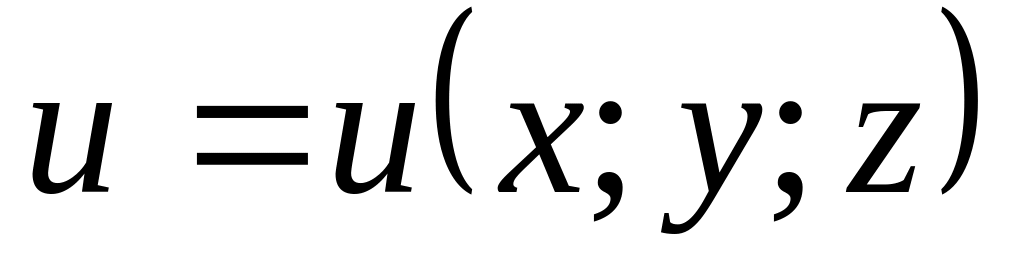в точці
за напрямком вектора
.
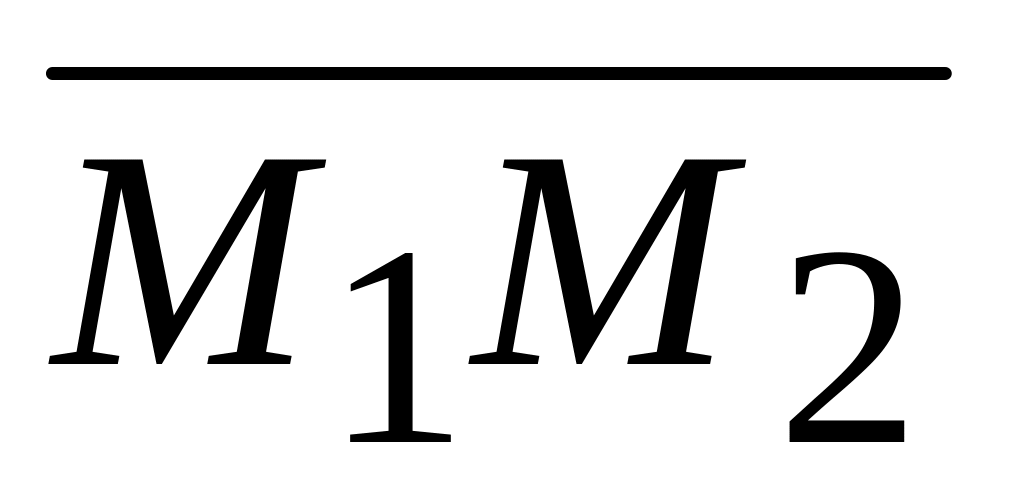. Відповідь:
.
Для векторного поля
,
та точки
,
знайти:
Відповідь:
За допомогою формули Остроградського-Гауса знайти течію векторного поля
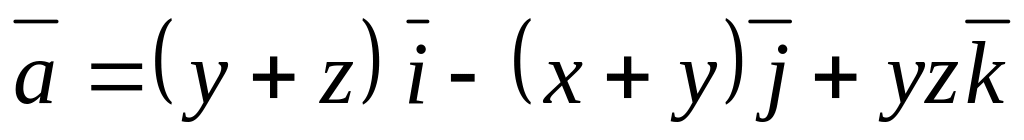через замкнену поверхню
.
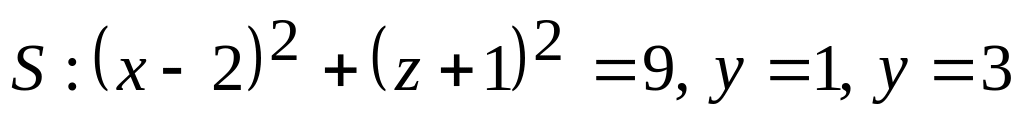Відповідь: 18.
Застосувавши формулу Стокса знайти циркуляцію векторного поля
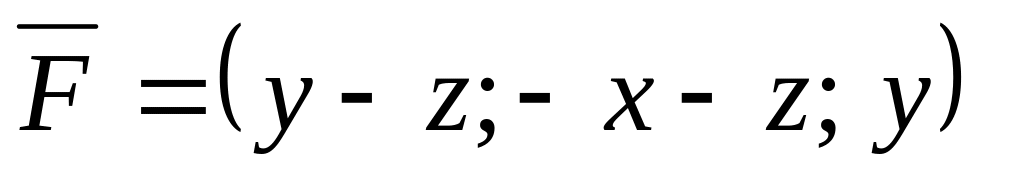по замкненому контуру трикутника, який
утворюється в наслідок перетинів
координатних площин з площиною
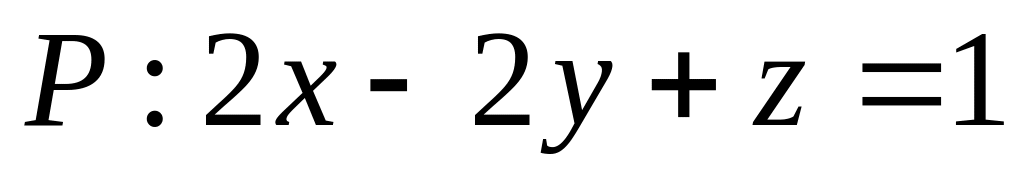(нормаль до трикутника
спрямована від початку координат).
Відповідь:
Довести, що поле
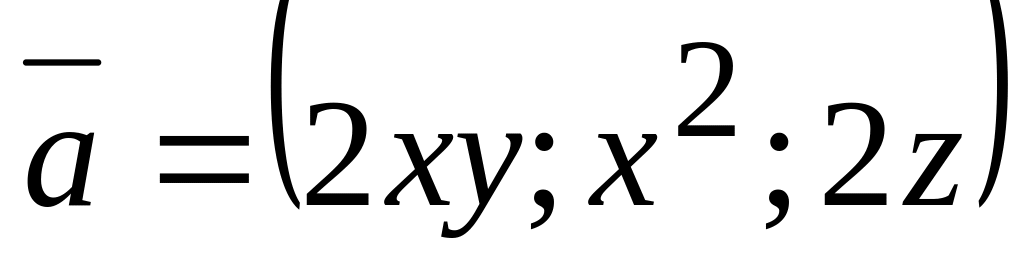є потенціальним та знайти його
потенціал. Відповідь:
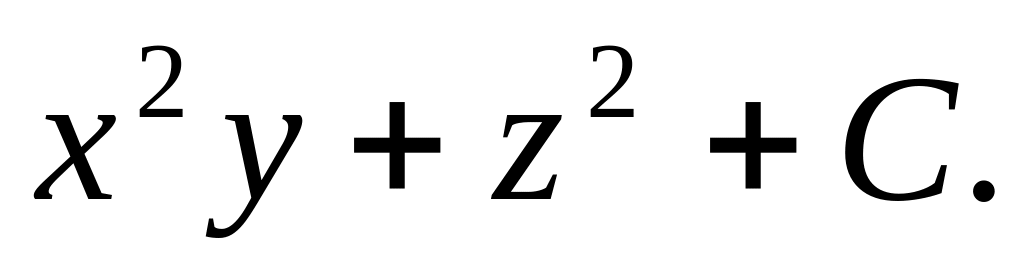
1.2 Варіанти індивідуальних завдань
1. Скалярне поле визначене функцією . Знайти його градієнт та побудувати поверхню рівня .
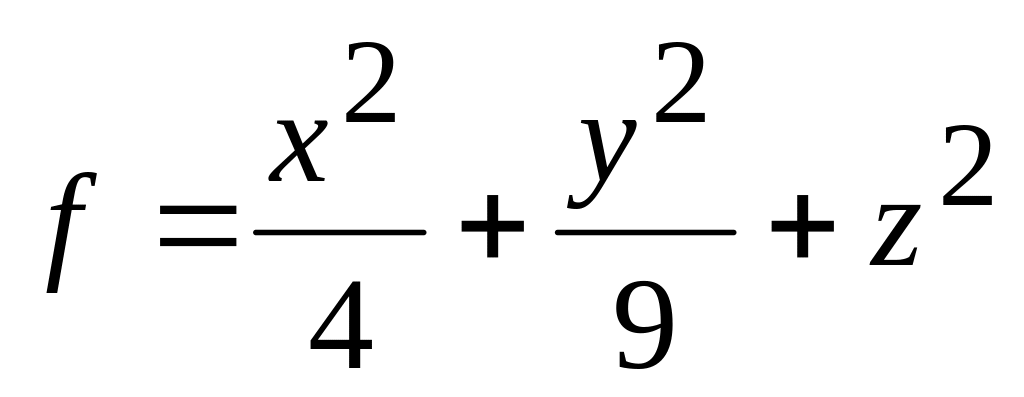. 2.
.
3.
. 4.
.
5.
. 6.
.
7.
. 8.
.
9.
. 10.
.
11.
.
12.
.
13.
. 14.
.
15.
. 16.
.
17.
. 18.
.
19.
. 20.
.
21.
. 22.
.
23.
. 24.
.
25.
. 26.
.
27.
. 28.
.
29.
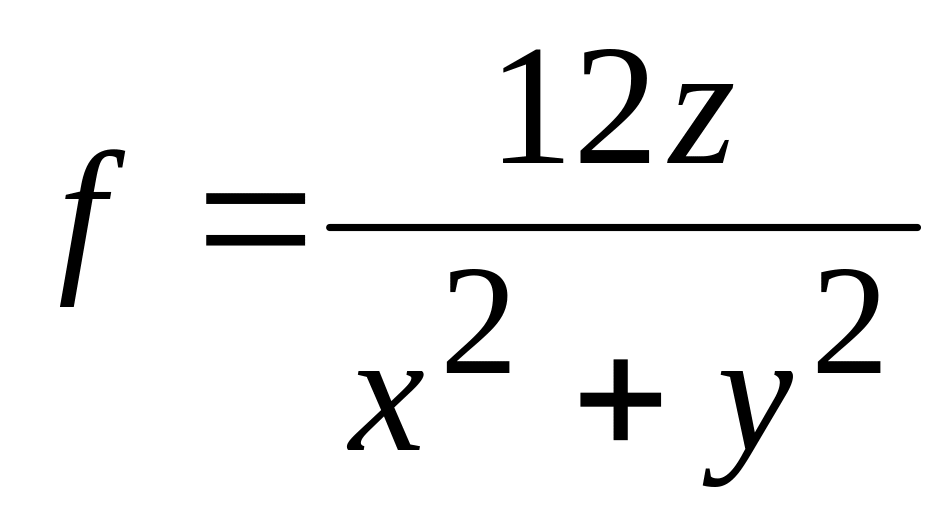. 30.
.
2. Знайти значення похідної функції в точці за напрямком вектора .
1.
.
2.
.
3.
.
4.
.
5.
.
6.
.
7.
.
8.
.
9.
.
10.
.
11.
.
12.
.
13.
14.
.
15.
.
16.
.
17.
.
18.
.
19.
.
20.
.
21.
.
22.
.
23.
.
24.
.
25.
.
26.
.
27.
.
28.
.
29.
.
30.
.
3. Для векторного поля
знайдіть:
1.
, 
2.
, 
3.
, 
4.
, 
5.
, 
6.
, 
7.
, 
8.
, 
9.
, 
10.
, 
11.
, 
12.
, 
13.
, 
14.
, 
15.
, 
16.
, 
17.
, 
18.
, 
19.
, 
20.
, 
21.
,
22.
, 
23.
, 
24.
, 
25.
, 
26.
, 
27.
, 
28.
,
29.
, 
30.
, 
4.
За допомогою формули
Остроградського-Гауса знайти течію
векторного поля
через зовнішню поверхню тіла, обмеженого
.
1.
,
2.
,
3.
,
4.
,
5.
,
6.
,
7.
,
8.
,
9.
,
10.
,
11.
,
12.
,
13.
,
14.
,
15.
,
16.
,
17.
,
18.
,
19.
,
20.
,
21.
,
22.
,
23.
,
24.
,
25.
,
26.
,
27.
,
28.
,
29.
,
30.
,
5.
Застосувавши формулу
Стокса знайти циркуляцію векторного
поля
по замкненому контуру трикутника, який
утворюється в наслідок перетинів
координатних площин з площиною
(нормаль до трикутника спрямована від
початку координат).
1.
,
2.
,
3.
,
4.
,
5.
,
6.
,
7.
,
8.
,
9.
,
10.
,
11.
,
12.
,
13.
,
14.
,
15.
,
16.
,
17.
,
18.
,
19.
,
20.
,
21.
,
22.
,
23.
,
24.
,
25.
,
26.
,
27.
,
28.
,
29.
,
30.
,
6. Довести, що поле є потенціальним та знайти його потенціал.
1.
,
2.
,
3.
,
4.
, 5.
,
6.
, 7.
,
8.
, 9.
,
10.
,
11.
,
12.
,
13.
, 14.
,
15.
,
16.
,
17.
, 18.
,
19.
, 20.
,
21.
, 22.
,
23.
, 24.
,
25.
, 26.
,
27.
, 28.
,
29.
, 30.
.