2.3. Оператори задання кіл (16 – методів).

2.3.1. Коло, задане координатами центра і радіусом.

С – ім’я > Х_цен, Y_цен, R

C 1 > 25, 20, 20

2.3.2. Коло, центр якого в т. Р – ім’я з радіусом R.

С – ім’я > Р – ім’я, R

C 1 > P2, 20

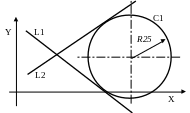
2.3.3. Коло, радіусом R і дотичне до двох прямих, які перетинаються.

С – ім’я > L – ім’я, {XM, XB, YB, YM}, L – ім’я {ХМ, YМ, ХВ, YВ}, R

Модифікатори уточнюють положення центра кола відносно прямих

C1 > L1, YB, L2, YM

2.3.4. Коло, задане радіусом і дотичне до прямої і іншого кола.

С – ім’я > L – ім’я, {ХМ, YМ, ХВ, YВ}, (QUT, IN), С – ім’я {ХМ, YМ, ХВ, YВ}, R

Перший модифікатор уточнює положення заданого (нового) кола відносно прямої. Положення (QUT, IN) уточнює, чи буде коло яке задаємо, знаходитись поза заданим. Поза – QUT, в середині IN. Другий модифікатор уточнює положення нового кола відносно центра заданого кола.

П риклад С₂ > L1, YМ, QUT, С1, ХВ 2

C1 > L2, YB, QUT, C2, XB, 25

1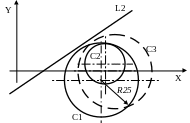 > L2, XM, IN, C2,YM, 25

C3 > L2, XB, IN, C2, YM, 25

C1 > L2, XM, QUT, C2, YM, 25

2.3.5. Коло, заданого радіуса і дотичне до двох інших кіл.

С – ім’я > С – ім’я, (QUT, IN), С – ім’я (QUT, IN), {ХМ, YМ, ХВ, YВ}, R

QUT, IN₁ – уточнюють положення нового кола всередині чи зовні відносно першого кола;

QUT, IN₂ – уточнюють положення нового кола всередині чи зовні відносно другого кола;

Модифікатори {ХМ, ХВ, YМ, YВ} уточнюють положення нового центра кола відносно уявної прямої, яка з’єднує центри двох заданих кіл

Приклад С3 > С1, QUT, С2, IN, YB, 30

2.3.6. Коло, утворене перенесенням заданого кола по координатах Х, Y.

С – ім’я > С – ім’я, Х, Y

C2 > C1, 40, -15

2.3.7. Коло, яке симетричне до заданого відносно заданої прямої.

С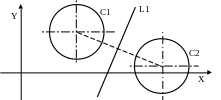 – ім’я > С – ім’я, L – ім’я

C2 > C1, L1

2.3.8. Коло, зовнішнє або внутрішнє по відношенню до заданого.

С – ім’я > С – ім’я, R

C2 > C1, 10

C3 > C1, -10

2.3.9.Коло, яке отримане шляхом повороту кола на кут відносно осі координат.

С – ім’я > С – ім’я, ANG, кут

C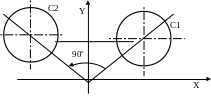 2 > C1, ANG, 90

2.3.10. Коло, яке проходить через дві задані точки заданого радіуса.

С – ім’я > Р1 – ім’я, Р2 – ім’я {ХМ, ХВ, YМ, YВ}, радіус

{ } – модифікатори уточнюють розміщення центра відносно уявної прямої, що проходить через дві задані точки.

2.3.11. Коло, що проходить через три задані точки.

С – ім’я > Р1 – ім’я, Р2 – ім’я, Р3 – ім’я

C1 > P1, P2, P3

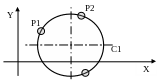
Р3

2.3.12. Коло заданого радіуса і дотичне до прямої, L проходить через задану точку.

С – ім’я > L – ім’я, Р – ім’я, {ХМ, ХВ, YМ, YВ}, радіус

Приклад С1 > L1, Р1, ХВ, 20

2.3.13. Коло, задане центром і дотичне до другого кола.

С – ім’я > Р – ім’я, С – ім’я, {LT, GT}

Модифікатори LT, GT уточнюють одне із двох можливих кіл. LT – менше коло, GT – більше коло.

C1 > P1, C2, LT

C 3 > P1, C2, GT

2.3.14. Коло, задане центром в заданій точці і заданою точкою на тому ж колі.

С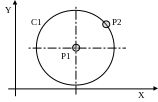 – ім’я > Р – ім’я, Р – ім’я,

C1 >P1, P2

2.3.15. Коло, задане існуючим колом (Перейменування).

С – ім’я > С – ім’я

2.3.16. Коло, заданого радіуса, яке проходить дотично до початку (кінця) контуру.

С – ім’я > (STK, ETK), К – ім’я, (RT, LF), радіус

(STK, ETK) – дотик в початку контуру – кінця контуру

К – ім’я – ім’я контуру

(RT, LF) – дотик справа чи зліва контуру

радіус – радіус нового кола

C 1 > STK, K1, LF, 15

C2 > ETK, K1, RT, 15