2.12. Багатокрокові схеми розв’язування задачі Коші

При підвищенні порядку однокрокових методів зростає кількість обчислень значень функції на кожному кроці, що спричинює збільшення обчислювальної роботи, особливо у випадку розв’язування систем звичайних диференціальних рівнянь високого порядку.

Щоб зменшити кількість обчислень правої частини на кожному кроці і при цьому забезпечити високий порядок точності, застосовують багатокрокові схеми.

При інтегруванні жорстких систем ЗДР на великих інтервалах зміни незалежної змінної явні методи Рунге-Кутта стають неефективними.

Узагальнено клас таких -крокових методів лінійних щодо подамо у вигляді:

(12.1)

де – числові коефіцієнти, .

До цих методів належать традиційні багатокрокові методи Адамса, методи Гіра та їхні модифікації. Дійсні коефіцієнти визначаються використовуваним методом.

Схему (12.1) називають явною (екстраполяційною), якщо і визначається через попередні значення за явною формулою:

. (12.2)

Щоб знайти , треба задати початкове значення , а їх можна визначити однокроковим методом. При рівняння (12.1) стає неявним щодо . Запишемо (12.1) у вигляді:

(12.3)

У цьому випадку є вектором наближеного розв’язку системи ЗДР (1.3), (1.4) у точці .

Для розв’язування нелінійної системи рівнянь (12.3) застосовують методи простої ітерації, Ньютона та його модифікації.

Ітераційний процес Ньютона можна відобразити рівнянням:

(12.4)

де

– матриця Якобі. (12.5)

Серед модифікацій методу Ньютона використовують такі, в яких матриця Якобі обчислюється чисельним диференціюванням.

У методі простої ітерації

, (12.6)

де – одинична матриця.

При використанні будь-якого ітераційного методу потрібно знати початкове наближення – предиктор (прогноз), який визначається з точністю порядку на підставі відомої інформації про попередні значення функції та її похідні , що використовуються у методі (12.4). За прогнозованим значенням з допомогою диференціального рівняння знаходять похідну , яку згодом підставляють у формулу корекції (12.4) для обчислення уточненого значення . В свою чергу використовують для отримання точнішого значення похідної . Якщо це значення похідної недостатньо близьке до попереднього, тоді це значення вводять у формулу корекції та ітераційний процес продовжується. Якщо похідна змінюється у припустимих межах, тоді значення використовується для остаточного обчислення . Після цього процес продовжується – робимо наступний крок, на якому обчислюємо .

Подамо функціональну схему алгоритму “прогноз” – “корекція”(рис.12.1).

–__

Рис. 12.1. Схема алгоритму прогнозування і корекції

2.13. Методи Адамса побудови багатокрокових схем

2.13.1. Екстраполяційний метод Адамса

Розглянемо праву частину рівняння (2.1) не на всій площині зміни її аргументів, а лише на кривій , що відповідає шуканому розв’язку. Нехай вже відомий наближений розв’язок у деяких точках сітки . Тоді у цих точках можна обчислити . Зробимо заміну . Замінимо функцію як суму інтерполяційного многочлена, який запишемо у формі Ньютона, і залишкового члена:

(13.1)

де

.

Оскільки точки не належать проміжку інтегрування , то заміна функції інтерполяційним многочленом буде екстраполяцією. Для обчислення розв’язку в наступній точці запишемо диференціальне рівняння в інтегральній формі:

. (13.2)

Підставляючи вираз (13.1) під знак інтеграла у формулу (13.2) і виконуючи необхідні інтегрування, одержуємо:

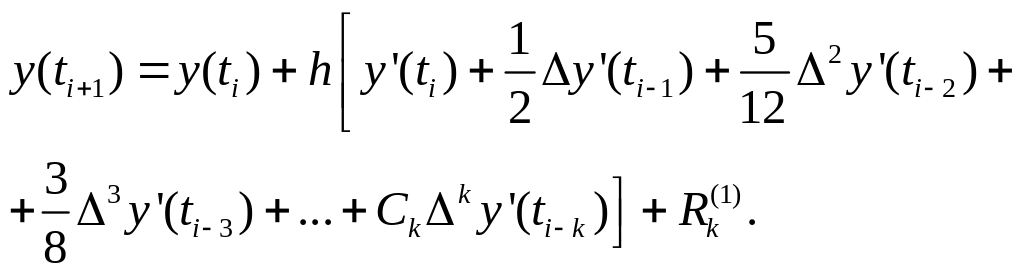(13.3)

Тут

(13.4)

Оскільки в останньому інтегралі функція зберігає знак на відрізку [0,1], то на основі узагальненої теореми про середнє значення при припущенні неперервності функції запишемо у вигляді:

(13.5)

Введемо позначення . Тоді:

. (13.6)

Якщо крок малий, то величиною в (13.3) нехтуємо і одержуємо правило екстраполяційного методу Адамса:

(13.7)

де коефіцієнти визначають за формулою (13.4). Числові значення коефіцієнтів наведемо у таблиці 30.

Таблиця 30

Коефіцієнти явних методів Адамса

	0	1	2	3	4	5	6	7	8
	1

Коефіцієнти задовольняють рекурентному співвідно-шенню [7]

. (13.8)

Запишемо часткові випадки формули (13.7) для . Враховуючи, що

а , отримаємо наступні формули: (13.9)

При ми маємо явний метод Ейлера і побудова початкової таблиці не потрібна. Формулу (13.7) часто приписують Адамсу і Башфорту.

Вибір та необхідно узгодити з потрібною точністю результату. Оцінка (13.5) мало придатна для рекомендацій до вибору цих величин, тому що, по-перше, вона містить відомості про похідні високого порядку від вихідного розв’язку, по-друге, вона характеризує локальну похибку значення без урахування накопиченої похибки та похибки округлень. На практиці параметри та намагаються задати так, щоб перший відкинутий доданок у (13.7) вже не впливав на результат у межах прийнятої точності.