§ 8. Работа различных процессов

Под названием работы объединяются многие энергетические процессы; общим свойством этих процессов является затрата энергии системы на преодоление силы, действующей извне. К таким процессам относится, например, перемещение масс в потенциальном поле. Если движение происходит против градиента силы, то система затрачивает энергию в форме работы; величина работы положительна. При движении по градиенту силы система получает энергию в форме работы извне; величина работы отрицательна. Такова работа поднятия известной массы в поле тяготения. Элементарная работа в этом случае:

W = – mgdH

где m – масса тела; H – высота над начальным нулевым уровнем. При расширении системы, на которую действует внешнее давление P, система совершает работу , элементарная работа равна в этом случае PdV (V₁ и V₂ – начальный и конечный объёмы системы соответственно).

При движении электрического заряда q в электрическом поле против направления падения потенциала  и на участке, где изменение потенциала равно d, а также при увеличении заряда тела, имеющего потенциал , на величину dq работа совершается над системой, величина ее равна в первом случае – qd, а во втором случае – dq.

Аналогичным образом можно выразить работу увеличения поверхности раздела S между однородными частями системы (фазами): W = -dS, где  – поверхностное натяжение.

В общем случае элементарная работа W является суммой нескольких качественно различных элементарных работ:

W = PdV – mgdH – dS – dq + … (1,9)

Здесь P, -mg, -σ, - – силы в обобщенном смысле (обобщенные силы) или факторы интенсивности; V, H, S, q – обобщенные координаты или факторы емкости.

В каждом конкретном случае следует определить, какие виды работы возможны в исследуемой системе, и, составив соответствующие выражения для W, использовать их в уравнении (I, 2а). Интегрирование уравнения (I, 9) и подсчет работы для конкретного процесса возможны только в тех случаях, когда процесс равновесен и известно уравнение состояния.

Для очень многих систем можно ограничить ряд уравнения (I, 9) одним членом – работой расширения.

Работа расширения при равновесных процессах выражается различными уравнениями, вытекающими из уравнения состояния. Приведем некоторые из них:

1) Процесс, протекающий при постоянном объёме (изохорный процесс; V = const):

W = ∫δW = ∫PdV = 0 (I, 10)

2) Процесс, протекающий при постоянном давлении (изобарный процесс; P = const):

W =  = P(V₂ – V₁) = PV (I, 11)

3) Процесс, протекающий при постоянной температуре (изотермический процесс, T = const). Работа расширения идеального газа, для которого PV = RT:

W = 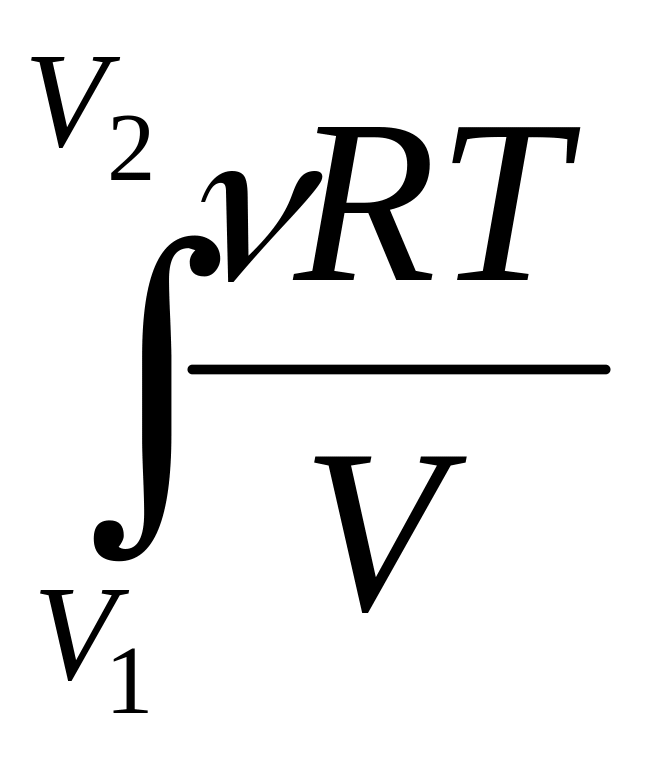dV = RT ln (I, 12)

§ 9. Теплоемкость. Вычисление теплоты различных процессов

Опытное определение удельной (с) или мольной (С) теплоёмкости тела заключается в измерении теплоты Q, поглощаемой при нагревании одного грамма или одного моля вещества на один градус при тех или иных условиях (постоянство давления или объёма или иные условия). При этом находят средние теплоёмкости в интервале температур T₁T₂:

= = (I, 13)

Истинные теплоемкости связаны со средними теплоёмкостями соотношением:

C_P =  ₌ и C_V =  ₌ (I, 14)

Истинные теплоемкости вычисляются из средних.

Зависимость теплоёмкости от температуры не может быть определена через другие свойства вещества на основании законов термодинамики. Она изучается экспериментально, теория же этой проблемы разрабатывается методами квантовой статистической физики.

Ход теплоемкостей в широком интервале температур охватывается обычно эмпирическим степенным рядом:

C_P = a + bT + сT² (I, 15)

Для значительного количества индивидуальных веществ значения коэффициентов a, b, с определены и приводятся в справочных таблицах.

Из уравнения (I, 14) следует:

(I, 16)

Проинтегрируем это выражение с учетом (I, 15):

(I, 17)

Полученная формула дает возможность вычислить теплоту любого процесса, связанного с изменением температуры в заданном интервале, если известна функциональная зависимость теплоёмкости от температуры.

Полученная формула также даёт возможность вычислить значение средней теплоёмкости в заданном интервале температур, если известна истинная теплоёмкость:

= (I, 18)

Попробуем решить обратную задачу нахождения истинной теплоёмкости по значению средней теплоёмкости. Из уравнений (I, 13) и (I, 14) следует:

и .

Если принять, что и обозначить как переменный параметр Т, то окончательно получим:

(I, 19)

Таким образом, если известна функциональная зависимость средней теплоёмкости от температуры, то её подстановкой в (I, 19) и последующим дифференцированием по температуре легко найти истинную теплоёмкость.

Существует квантовая теория теплоёмкостей твёрдого тела П.Дебая, которая является приближённой общей теорией, основанной на использовании методов статистической механики.

По теории Дебая, теплоёмкость C_V чистого твёрдого тела определяется формулой

, где - некая функция отношения так называемой характеристической температуры  (температуры Дебая) и абсолютной температуры Т. Характеристическая температура может быть определена различными методами (по спектрам вещества, по его сжимаемости), а также вычислена по ряду полуэмпирических уравнений (уравнение Линдемана для одноатомных веществ и др.). Величина  имеет размерность температуры и зависит в основном от химического состава твёрдого тела и в очень малой степени от давления.

Анализ уравнения, предложенного Дебаем, показывает, что при высоких значениях Т молярная теплоёмкость твёрдых тел = 25 . То, что теплоёмкости моноатомных твёрдых тел стремятся к одному и тому же значению, было замечено задолго до Дебая; это явление получило название закона Дюлонга-Пти.

В области низких температур:

(I, 20)

Это уравнение выражает известный закон Т-кубов Дебая, согласно которому при приближении к абсолютному нулю теплоёмкость пропорциональна температуре в третьей степени. Экспериментально было показано, что это верно для многих твёрдых тел.