21. Гармониялық тербелістердің негізгі сипаттамалары. Тербелімелі қозғалысты сипаттайтын негізгі үғымдарды енгізгеннен кейін гармониялық тербелістер ұғымы енгізіледі.

Гармониялық тербеліс ұғымын енгізу үшін 14-суретте көрсетілген қондырғы серіппелі маятникті қолдануға болады. Бұл тәжірибеде төменгі бөлігінде тесігі бар кішкене ыдысқа құм (немесе боялған сұйық құйылған) салынған, оны тербелмелі қозғалысқа келтіріп; тербеліс жазықтығына перпендикуляр бағытта таспаны тұрақты жылдамдықпен жылжытсақ, онда таспада толқын тәрізді із қалады.

       14 –сурет                                     15-сурет

15-суретте алынған қисықтың түрі көрсетілген. Ол синусоида деп аталады.

Егер қандай да бір дене координатасының уақытқа тәуелді графигі синусоида (косинуоида) болса, яғни координата уақыт өтуіне байланысты синус (косинус) заңымен өзгерсе, онда мұндай жағдайда координата да, дене де гармониялық тербеліс жасайды.

Физикалық шамалардың уақыт өтуіне байланысты синус және косинус заңы бойынша периодты өзгеруі гармониялық тербеліс деп аталады. Әртүрлі периодты процесстерді (бірдей уақыт мезетінде қайталанып отыратын процесстер) гармониялық тербелістердің қосындысы (суперпозиция) түрінде беруге болады.

s шамасының гармониялық тербеліс теңдеуі мынадай түрде болады:

s=Acos(ωt+φ). Мұндағы А –тербеліс амплитудасы-жүйенің тепе-теңдік қалпынан ең үлкен ауытқуы;

ω-дөңгелектік (циклдік) жиілік

φ-тербелістің t= 0 уақыт мезетіндегі бастапқы фазасы. (ωt+φ) –тербелістің t уақыт мезетіндегі фазасы.

Тербеліс фазасы тербелмелі шамалардың берілген уақыт мезетіндегі мәнін анықтайды. Косинус +1ден -1 аралығанда өзгеретіндіктен, s мәнінің +А дан –А-ға дейінгі аралықта жатады. Яғни осы параметрлер гармониялық тербелістердің негізгі сипаттамаларын бейнелейді.

: cos(α+2π)= cosα болғандықтан, 2π бүтін санын фазаға қосқанда немесе одан алып тастағанда гармониялық тербеліс кезінде х-мәні өзгермейді. Толық бір тербеліс үшін кеткен уақыт аралығымен өлшенетін шама тербеліс периоды деп аталады және тербеліс фазасы 2π-ге өсімше қабылдайтындықтан:

ω(t+T)+φ=(ωt+φ)=2π және осыдан

T=

Периодқа кері шама, бірлік уақыт ішіндегі тербеліс саны n тербеліс жиілігі деп аталады

Тербеліс жиілігінің өлшем бірлігі –герц (Гц) периодты процестің жиілігі –периодты 1 секундқа тең келетін тербеліс санымен өлшенеді.

22. Гармониялық тербелістердің энергиясы. Тербелімелі қозғалысты сипаттайтын негізгі үғымдарды енгізгеннен кейін гармониялық тербелістер ұғымы енгізіледі.

Гармониялық тербеліс ұғымын енгізу үшін 14-суретте көрсетілген қондырғы серіппелі маятникті қолдануға болады. Бұл тәжірибеде төменгі бөлігінде тесігі бар кішкене ыдысқа құм (немесе боялған сұйық құйылған) салынған, оны тербелмелі қозғалысқа келтіріп; тербеліс жазықтығына перпендикуляр бағытта таспаны тұрақты жылдамдықпен жылжытсақ, онда таспада толқын тәрізді із қалады.

       14 –сурет                                     15-сурет

15-суретте алынған қисықтың түрі көрсетілген. Ол синусоида деп аталады.

Егер қандай да бір дене координатасының уақытқа тәуелді графигі синусоида (косинуоида) болса, яғни координата уақыт өтуіне байланысты синус (косинус) заңымен өзгерсе, онда мұндай жағдайда координата да, дене де гармониялық тербеліс жасайды.

Физикалық шамалардың уақыт өтуіне байланысты синус және косинус заңы бойынша периодты өзгеруі гармониялық тербеліс деп аталады. Әртүрлі периодты процесстерді (бірдей уақыт мезетінде қайталанып отыратын процесстер) гармониялық тербелістердің қосындысы (суперпозиция) түрінде беруге болады.

Тепе-тендік қалып пен үлкен ауытқудың екі аралығывда кез келген күштерде дененің кинетикалық әрі потенциалдық энергиясы болады, бірақ олардың қосындысы, яғни толық энергия дененің кез келген қалпында -ге тең болады. Тербелуші дененің толық энсргиясы  W оның тербелістерінің амплитудасының квадратына пропорционал:

Механикалық энергияның сақталу заңын қолдана отырып, серіппелі және математикалық маятниктер үшін периодтың формуласы

қорытылып шығарылады.

23. Еріксіз тербелістер. Егер денеге сыртқы периодты күш әсер етсе, онда дене осы күш жиілігімен тербелетін болады. Бұндайда тербеліс амплитудасы уақытқа, дене тербелісінің меншікті жиілігіне, өшу коэффициентіне және мәжбүр етуші күш жиілігіне F_ocos wt тәуелді. Уақыттың бастапқы мезетінде амплитуда шамасына меншікті жиілік ықпал етеді– тербеліс амплитудасының периодты өзгеруі, яғни соғу пайда болады. Тек белгілі бір уақыт өткен соң

тербеліс амплитудасы орнығады.

Меншікті жиілік пен мәжбүр етуші күш жиілігі сәйкес келгенде тербеліс амплитудасы күрт өседі. Жиіліктер сәйкес келгендегі амплитуданың өсуі резонанс деп аталады. Резонанс кезіндегі тербеліс амплитудасының шектелуі екі себеппен анықталады: кедергі күшінің болуы (өшу коэффициенті) және меншікті жиілік пен мәжбүр етуші күш жиілігінің арасындағы айырмаға әкелдіретін амплитуданың жиілікке тәуелділігі.

Еріксіз тербеліс — қандай да бір жүйеде периодты сыртқы күштің әсерінен пайда болатын тербеліс (мысалы, айнымалы магнит өрісі әсерінен болатын телефон мембранасының тербелісі, т.б.). Еріксіз тербелістің сипаты сыртқы күштің табиғаты мен жүйенің өзіне тән қасиеттері арқылы анықталады. Сыртқы күштің болуы — еріксіз тербелістің қозуы мен болуының қажетті шарты. Периодты сыртқы күштің әсерінен еріксіз тербелістің сипаты алғашқы кезде уақытқа байланысты өзгереді. Тек белгілі бір уақыт өткеннен кейін, жүйеде периодты сыртқы күштің периодына тең еріксіз тербеліс қалыптасады (орныққан еріксіз тербеліс). Дербес жағдайда, сыртқы күштің (жиілігі жүйенің меншікті тербеліс жиілігіне жуық) әсерінен сызықтық тербелмелі жүйеде еріксіз тербеліспен бір мезгілде меншікті (еркін) тербеліс пайда болады. Тербелістің бастапқы сәтінде ол тербелістердің амплитудалары бір-біріне тең де, ал фазалары қарама-қарсы болып келеді (суретті қ.). Сөйтіп, меншікті тербеліс біртіндеп өшкен соң, жүйеде тек орныққан еріксіз тербеліс қалады. Сондықтан тербелмелі жүйеде меншікті тербеліс неғұрлым ертерек өшсе, солғұрлым сол жүйеде орныққан еріксіз тербеліс тезірек қалыптасады. Еріксіз тербелістің амплитудасы әсер етуші күштің амплитудасы мен жүйедегі меншікті тербелістің өшу дәрежесіне байланысты анықталады. Егер меншікті тербелістің өшу дәрежесі аз болса, онда еріксіз тербелістің амплитудасы әсер ету күшінің жиілігі мен жүйенің меншікті тербеліс жиілігінің ара қатысына едәуір дәрежеде тәуелді. Сыртқы күштің жиілігі жүйенің меншікті жиілігіне жуықтаған кезде еріксіз тербелістің амплитудасы кенет артып, резонанс құбылысы пайда болады. Сызықтық емес жүйелерде тербелісті меншікті тербеліске және еріксіз тербеліске ажырату әрдайым мүмкін бола бермейді.

24. Гюйгенс-Френель принципі. Жарықтың толқындық сипаты білінетін құбылыстардың біреуі дифракция құбылысы болады. Дифракция деп жарықтың түзу сызықты жолдан бұрылу құбылысы айтылады.Дифракция құбылысын жарықтың толқындық теориясы бойынша толық түсіндіруге болады. Бірақ ол үшін Гюйгенс принципі жеткіліксіз. Өйткені бұл принципке сүйеніп дифракцияланған жарық толқындарының интенсивтігін табуға болмайды,бұл принцип тек жарықтың таралу бағытын анықтау әдісі болып табылады.Френель бұл принциптің осы кемшілігін толықтырды,ол Гюйгенстің принципі мен толқындардың интерференциялану принципін біріктірді. Френельше толқындық беттің әрбір нүктелерінің айналасында пайда болған элементар толқындар бір-бірімен қосылысып интерференцияланады,сонда қорытқы сыртқы орауыш бетте толқынның едәуір интенсивтігі болады. Сөйтіп жарықтың толқындық теориясының негізгі принципі- Гюйгенс-Френель принципі келіп шығады.

1. Кез-келген уақыт мезетіндегі толқындық бет дегеніміз-айналып өтетін екінші ретті толқындардың жай ғана өзі емес, олардың интерференцияларының нәтижесі болып табылады.

2. Жарық толқындары келiп жеткен беттiң әрбiр нүктесi өз кезегiнде жаңа толқын көздерi болып табылады Тамаша оптикалық аспаптың-дифракциялық тордың құрлысы дифрациялық құбылысқа негізделген.

Гюйгенс принципі түсіндіре алмайтын жарықтың түзу сызық бойымен таралу заңын Гюйгенс-Френель принципі бойынша түсіндіруге болатын. Бұл мәселені ең алғаш 1815 жылы Френель шешкен болатын. Ол күрделі есеп шығарудың орнына зоналар әдісі деп аталатын көрнекі тәсіл қолданды. 3-суретте көрсетілген S жарық көзінен жарық толқындары таралып сфералық толқындық беттер түзілсін, сонда олардың біреуі  - мен белгіленген бет болсын. Енді жарық толқынының Р нүктедегі әсерін анықтау үшін Френельше сол  толқындық бетті ойша дөңгелек зоналарға бөлеміз. Егер РО аралығын  әріпімен белгілесек, ол сфералардың радиустары мынадай болады: 11.3-сурет Френель зоналарын салу Жарықтың параллель шоғы тар саңылаудан өткенде байқалатын дифракциялық жолақтар едәуір жалпақ болады. Егер жарық бір саңылаудан емес, қатарласқан бірнеше саңылаудан өткізілсе, онда байқалатын дифракциялау жолақтар енсіз және жарығырақ болады. Енділігі бірдей, өзара параллель орналасқан саңылаулар жиыны әдетте дифракциялық решетка деп аталады. Төмендегі суретте жазық мөлдір решетка схема түрінде кескінделген. Мұнда тек решетканың төрт саңылауы көрсетілген, олардың енділіктері бірдей:   мөлдір емес аралық енділіктері де бірдей:   Осы a мен b қосындысы: a+b=d – решетка тұрақтысы деп аталады.

25. Сфералық толқындардың (Френель дифракциясы ) дифракциясы. Жарықтың дифракциясы деп жарық толқындарының жолындагғы бөгетті орап (айналып) өтуін айтады. Неғұрлым кең мағынада айтқанда, электромагниттік толқындар экранның саңлаудың немесе басқада да біртекті емес нәрселердің шетіне жақын жерден өткенде олардың таралу бағыты өзгереді.Жарық дифракциясының сфералық толқындар дифракциясы (Френель дифракциясы) және параллель сәулелер дифракциясы (Фраунгофер дифракциясы) деп аталатын екі түрі бар. Френел бойынша нүктелік көзбен қоздыратын жарық толқыны толқындық беттің элементтерімен сәулеленетін когерентті екінші ретті толқындардың суперпозиция нәтижесі ретінде қарастырыла алады. Толқындық беттің зоналарға бөлінуі екі көршілес зоналардан шығатын толқындардың оптикалық жүріс айырмасы Р бақылау нүктесінде тең болатын және бұл толқындар Р нүктесіне кері фазалармен келеді де, жартылай бір бірін сөндіреді.

Бірін бірі ауыстыратын жарық және қара концентрлік сақиналардан тұратын, Френел зоналардың орналасу принципі бойынша құрылған зоналық қабатшаны қолдану толқындық беттің бөлінуін эксперименталды дәлелдейді. Жарық және қара зоналардың саны болса, онда амплитуда нүктесінде тең:

(9.1)

Сол уақытта P нүктесінде амплитуда зоналық қабатшасыз тең (бірінші зонаның жартысының салымы). Сондықтан зоналық қабатшаны қолдану Р нүктесіндегі жарық интенсивтілігін коэффициентімен көбейтуге мүмкіндік береді. Бұл зоналық қабатшаны жинағыш линза ретінде қолдануға болатынын көрсетеді.

9.1-суретте зоналық қабатшаның бірінші сақиналарының жазық толқынмен жарықтандыруы көрсетілген. Р нүктесі және зоналық қабатшаның ортасымен қашықтығы болсын, онда Р нүктесі үшін радиустар үшін келесі теңдеу орындалады :

, мұнда , мұнда (9.2)

Сонымен , зоналық қабатшаның радиустары және фокустық қашықтық үшін:

(9.3)

9.1-сурет. Жазық толқынмен қабатшаның бірінші зоналарын жарықтандыруы

Егер Р бақылау нүктесін ОР бағытымен зоналық қабатшаға қарай жылжытсақ, онда жарық және қараңғы бейнелерді көруге болады, бұл зоналық қабатша бірнеше фокустары бар екенін көрсетеді.

(9.4)

Эксперимент үшін қолданылатын зоналық қабатшада 20 зона бар, бірінші ортасындағы қараңғы шеңбер радиусы . Сонымен келесі радиустар тең:

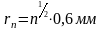(9.5)

Фраунгофер дифракциясының Френель дифракциясынан негізінде айырмашылығы жоқ.Шексіз ұзын, ені b саңылауға жазық жарық толқыны нормаль (тік) түсетін болсын (1-сурет). Саңылау ұзындығының оның енінен көп үлкен болуы іс жүзінде оны шексіз ұзын деп санауға жеткілікті. Мәселен, ені 0,001-0,02 мм болған жағдайда бірнеше миллиметр ұзындықты шексіз деп санауға болады.

С аңлаудан кейін линза, ал оның тоғыстық жазықтығына L бақылау қалқасы қойылған. Жарық түзу сызықты таралған жағдайда линзаның тоғыстық жазықтығында шексіз жіңішке жарық жолақ алынған болар еді. Шындығында толқындық шептің саңлауға жеткен әрбір нүктесі барлық жаққа таралатын екінші реттік толқындардың көзі болады. Жарықтың бастапқы бағытымен қайсыбір  бұрыш жасап тұратын сәулелер линзаның тоғыстық жазықтығындағы B_ нүктесіне жиналады.

Тербелістердің B_ нүктедегі амплитудасын есептеу үшін толқындық беттің ашық бөлігін ендері бірдей саңылау нүктелеріне параллель жіңішке жолақтар түріндегі аумақтарға бөлеміз. Осы аумақтардың әрқайсысы B_ нүктесіне келіп жететін толқындар көзі ретінде қарастырылуы тиіс, және көрші аумақтардан шығарылатын толқындардың фазалары бірдей шамаға өзгеше болады. Өйткені жарық нормаль (тік) бағытта түскенде саңылау жазықтығы толқын бетімен дәл келеді. Элементар толқындардың амплитудалары бірдей болады, өйткені аумақтардың аудандары тең және бақылау бағытына көлбеуліктері де бірдей.

Осы екі жағдай – амплитудалардың теңдігі және аумақтан аумаққа өткенде фазалардың бірдей шамаға өзгеруі – қарастырылып отырған есептің аналитикалық та, график арқылы да амалмен шешілуін оңайлатады.

1. Алдымен еcепті шешудің аналитикалық амалын қарастырайық. Ол үшін толқындық беттің бөлігін ені dx элементар аумақтарға бөлеміз. Қалқаның кезкелген нүктесінде dx аумағы қоздыратын тербелістің dA амплитудасын dA=сdx түрінде өрнектеуге болады, мұндағы с–пропорциялық коэффициент, ол  бұрышқа тәуелді емес.

Қалқаның қайсыбір нүктесіне барлық аумақтардан келетін тербелістер амплитудаларының алгебралық қосындысын А₀ арқылы белгілейміз. Мұны dA-ны түгел саңылау бойынша интегралдап табуға болады. .

Осыдан коэффициент , демек, болады. Сонымен, саңылаудың тиісті бөлігіндегі жарықтың ұйытқуы мына қатынаспен өрнектеледі

(1)

Түсетін толқын бағытымен  бұрыш (дифракция бұрышы) жасайтын бағытында саңылаудың түгелдей әрекетін табу үшін әртүрлі аумақтардан B_ бақылау нүктесіне дейін жететін толқындарды сипаттайтын фазалар айырымын ескеру қажет. Бұл үшін дифракцияланған сәулелердің бағытына перпендикуляр АD жазықтығын жүргіземіз (1-сурет). Осы жазықтықта орын алатын фазалардың үлестірілуі B_ нүктесіне дейін келіп жететін элементар толқындардың фазаларының қатынасын анықтайды. Сонымен AC жазықтығынан AD жазықтығына дейінгі жолда пайда болатын жол айырымын тағайындау жеткілікті болады. 1-суреттен А нүктесіне (аумақтың сол жақ шеті) және А нүктесінен х қашықтықта жататын қандайда бір F нүктесіне жапсарлас элементар аумақтан келетін толқындар арасындағы жол айырымы мынаған тең: FE=xsin.

B_ нүктесінде толқындық беттің барлық ашық бөлігі туғызатын қорытқы ұйытқу саңылаудың бүкіл ені бойынша алынған интегралмен (яғни х-тың 0-ден b-ға дейінгі барлық мәндері бойынша) өрнектеледі

(2)

( 2) өрнектегі косинустың алдында тұрған өрнектің модулі қорытқы толқынның В_ нүктедегі А_ амплитудасын береді:

(3)

(3) өрнегін зерттейік. Саңылаудың ортасында жататын нүкте үшін (линзаның центріне қарсы нүкте) дифракция бұрышы =0. (3) формуласына =0 мәнін қойып болатынын табамыз, яғни =0 болғанда барлық элементар аумақтардан шығарылатын толқындар B_ нүктеге бірдей фазада келіп жетеді. Сондықтан қорытқы толқынның амплитудасы қосылатын толқындардың амплитудаларының алгебралық қосындысына тең.

 мәндері мұндағы шартын қанағаттандыратын жағдайда, яғни егер

(4)

болған жағдайда А_ амплитуда нөлге айналады.

Сонымен, (4) шарты интенсивтік минимумдерінің орнын анықтайды. Бірінші минимум шартын қанағаттандыратын бұрышта байқалатын болады.

Минимумдердің араларында орталық максимумнан шамасы бойынша елеулі түрде кем түсетін интенсивтіктің екінші реттік максимумдары орналасады. Осы максимумдар  мәндері мына шарттарды

(5)

қанағаттандыратын жағдайда пайда болады.

Жарық интенсивтігі амплитуда квадратына пропорционал. Демек,

(6)

мұндағы I₀-дифракциялық суреттің ортасындағы жарық интенсивтігі ( ); I_- бұрышының берілген мәнімен орны анықталатын нүктедегі жарық интенсивтігі.

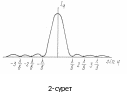
(6) функциясының графигі 2-суретте кескінделген. Минимумдар саны b-саңылау енінің және  толқын ұзындығының қатынасына тәуелді. Екінші реттік максимумдар шамасы тез төмендейді. Егер I₀=1 деп алсақ, ал екінші реттік максимумдарды I₁, I₂, I₃,... арқылы белгілесек, онда I₀: I₁: I₂:...=1:0,045:0,016:... болады. Сонымен, негізгі жарық ағыны (орталық максимум) мәндерімен анықталатын аралыққа шоғырланғанымен, оның қайсыбір бөлігі бірінші (энергияның ~5%) және екінші (энергияның ~2%) максимумдар және т.т. бағыттарында таралады.

Алынған қатынастардан максимумдар мен минимумдардың орны  толқын ұзындығына тәуелді болатындығы көрінеді. Сондықтан қарастырылған дифракциялық суреттің түрі тек монохромат жарық үшін орындалады. Ақ жарық жағдайында бірі екіншісіне қатысты  толқын ұзындығының айырмашылығына сәйкес ығысқан әртүрлі түстер үшін дифракциялық суреттердің жиынтығы байқалады. Орталық максимум (=0) барлық толқын ұзындықтары үшін ортақ болады, осыдан дифракциялық суреттің центрі ақ жолақ түрінде шығады, мұның сол және оң жақтарында түрлі-түсті жолақтар орналасады.

25. Дифракциялық тор.

Айқын да анық дифракциялық суретті алу және бақылау үшін дифракциялық торды пайдаланады. Дифракциялық тoр дегеніміз — жарық дифракциясы байқалатын тосқауылдар және саңылаулардың жиынтығы.

Дифракциялық торды реттелген дифракциялық тop және реттелмеген дифракциялық тop деп бөледі. Реттелген тор деп саңылаулары белгілі бір қатаң тәртіп бойынша орналасқан торларды, ал реттелмеген деп саңылаулары тәртіпсіз орналасқан торларды айтады. Геометриялық құрылысына қарай торларды жазық және кеңістіктік торлар деп те бөледі. Кеңістіктік реттелмеген торларға, мысалы, тұмандағы ауа тамшылары немесе мұз қиыршықтарының жиынтығы, көз кірпіктері жатады.

Оны алмаз кескішпен жасалған параллель және бір-біріне өте жақын орналасқан саңылаулар мен тосқауылдар жиынтығынан дайындайды. Саңылаудың ені а, ал тосқауыл-штрихтің ені b болсын, сонда b + a = d тордың тұрақтысы немесе периоды деп аталады.

Жарықтың дифракциялық торда таралу процесін карастырайық. Монохроматтық сәулеленудің жазық шебі тор саңылауларының жазықтығына жетті дейік. Линзаның көмегімен барлық параллель шоқтарды экранға жинаймыз. Экранда φ бағытында таралатын параллель сәулелердің шоқтары жиналатын кез келген А нүктесін таңдап аламыз. Көрші екі саңылаудан шығатын жарық сәулелерінің жол айырымын оңай табамыз: A = dsinφ.

Егер Δ = 2kλ/2 болса, А нүктесінде максимум байқалады. Онда дифракциялық тор үшін келесі формула дұрыс:

Бұл формула арқылы максимумдардың бірінші, екінші, т.с.с. қатарларын табуға болады. Дифракциялық көрініс — бұл күңгірт аралықтармен бөлінген түрлі-түсті жолақтар қатары. Саңылаудан ақ жарық жібергенде орталықтағы ақ дақтың екі шетінен бірінші, екінші, т.с.с. қатармен орналасқан боялған спектрлер көрінеді.

Сонымен бірге толқын ұзындығы артқан сайын (қызыл жарық) осы толқынның максимумы байқалатын бұрышы үлкен болады.

 Егер орға көк жарық түсірілсе, онда барлық максимумдар көк түске боялады

Жарық толқынының ұзындығын табу үшін аспаптың миллиметрлік бөліктері бар ұзын сызғыштың бір ұшына қарай оның бойымен еркін қозғалатын етіп экран орналастырылады. Экранның ортасында саңылау бар. Сызғыштың екінші ұшына дифракциялық торды орнатамыз.

Top және саңылау арқылы жарық көзіне қарасақ, онда біз экранның қара фонында саңылаудың екі жағынан дифракциялық спектрлердің бірінші, екінші және т.с.с. реттерін көреміз. Дифракциялық тордың формуласын пайдаланып және өте аз бұрыш үшін sinφ ~ tgφ деп алуға болатынын және tgφ = a/L екенін ескеріп, жарық толқынының ұзындығын есептейміз:

мұндағы d — тордың периоды, a — саңылаудан анықталатын толқын ұзындығы спектрінің сызығына дейінгі кашықтық, L — дифракциялық тордан экранға дейінгі сызғыш бойымен алғандағы қашықтық.

26. Резонанстық қисық. Фазалар ығысуы.

Резонанс (лат. resono, фр. resonance — үн қосу, дыбыс қайтару) — периодты түрде сырттан әсер етуші күштің жиілігі тербелмелі жүйенің меншікті жиілігіне жақындағанда сол тербелмелі жүйедегі еріксіз тербелістер амплитудасының күрт арту құбылысы; мәжбүр етуші күштің жиілігі жүйе тербелісінің меншікті жиілігіне жуықтаған кезде жүйедегі мәжбүр тербеліс амплитудасының кенеттен артып кету кұбылысы.

Резонансты алғаш рет механика және акустикалық құбылыс ретінде италиян ғалым Г.Галилей, ал электр-магниттік жүйелерде, мысалы, тербелмелі контур арқылы ағылшын ғалымы Дж.Максвелл (1831 — 1879) қарастырған (1868). 

Резонанс қисығы - мәжбүр тербелісті сипаттайтың кандай да бір параметрдің (амплитуданын, фазаның және т.б.) сырткы әсердің жиілігіне тәуелділік графигі.

Айнымалы ток тiзбегiнiң толық кедергiсi тек тiзбек элементтерiнiң параметрлерiнен ғана емес, сонымен қатар мәжбiрлеушi кернеудiң өзгеру жиiлiгiнен де тәуелдi. Яғни, жиiлiк өзгерген кезде толық кедергi де өзгередi. Тiзбектегi ток максимальдi болу үшiн, Ом заңына сәйкес, оның толық кедергiсi минимальдi болуы керек. Ал кедергiнiң мәнi

шарты орындалғанда минимальдi болатыны көрiнiп тұр. Бұл шартқа сәйкес келетiн сыртқы мәжбiрлеушi кернеудiң жиiлiгi

Ал бұл еркiн тербелмелi контурдың өшпейтiн еркiн тербелiсiнiң жиiлiгiне тең шама.

Олай болса, сыртқы мәжбiрлеушi кернеудiң жиiлiгi тербелмелi контурдың еркiн тербелiсiнiң жиiлiгiне сәйкес болғанда тiзбектегi токтың мәнi күрт артып кетедi екен. Осы құбылысты айнымалы ток тiзбегiндегi резонанс құбылысы деп атайды. Тiзбектiң актив кедергiсiнiң әртүрлi мәндерiндегi токтың амплитудалық мәнiнiң сыртқы мәжбiрлеушi кернеудiң жиiлiгiнен тәуелдiлiгi суретте келтiрiлген. Электр тiзбегiндегi резонанс құбылысы радиотехникада, оның iшiнде қабылдау схемаларында, күшейткiштерде, жоғарғы жиiлiктегi тербелiс генераторларында кеңiнен қолданылады.

Айнымалы токтың үш фазалық жүйесі жиі қолданылады. Тұрақты токқа қарағанда айнымалы токтың генераторлары мен қозғалтқыштарының құрылымы қарапайым, жұмысы сенімді, мөлшері шағын әрі арзан. Айнымалы ток әуелі шала өткізгіштер арқылы, ал одан кейін шала өткізгішті инверторлар көмегімен жиілігі реттелмелі басқа айнымалы токқа түрлендіріледі. Бұл жағдай жылдамдығын бірте-бірте реттеуді талап ететін электр жетектерінің барлық түрі үшін қарапайым әрі арзан қозғалтқыштарын (асинхронды және синхронды) пайдалануға мүмкіндік береді.

2-сурет.

Тәжірибеде жай және неғұрлым маңызды жағдайда айнымалы ток күшінің лездік мәні ( ) синусоидалық заңға сәйкес белгілі бір уақыт   ішінде мынадай заң бойынша өзгереді:

, мұндағы   — ток амплитудасы,  ƒ— токтың бұрыштық жиілігі,   — бастапқы фаза.

Сондай жиіліктегі кернеу де синусоидалық заң бойынша өзгереді:

, мұндағы   — кернеу амплитудасы,   — бастапқы фаза (2-сурет).

Мұндай айнымалы токтың әсерлік мәндері мынаған тең болады:

 ≈ 0,707  ,

 ≈ 0,707  .

Айнымалы ток тізбегінде индуктивтілік не сыйымдылықтың болуына байланысты ток күші ( ) мен кернеу ( ) арасында   фаза ығысуы пайда болады. Фаза ығысуы салдарынан ваттметрмен өлшенетін айнымалы токтың орташа қуаты ( ) әсерлік ток мәні мен әсерлік кернеу мәнінің көбейтіндісінен кем болады:

.