5. Материалдық нүкте мен қатты дене динамикасы

Нүктенің материялық екенін, яғни басқа денелерден айырмашылығы оның өлшемдері болмайтынын ұмытпаған жөн. Сонымен материялық нукте деп қозғалыстың қарастырылып отырган жағдайында өлшемдерін елемеуге болатын денені айтады. Шындығына келгенде, табиғатта ешқандай материялық нүкте жоқ. Ол нақты дененің ойдан алынған үлгісі болып табылады. Бұл ұғым механикадағы кейбір мәселелерді шешудін ыңғайлы әрі карапайым болуы үшін ғана енгізілген. Міне, жоғарыда келтірілген мысалдағы кеменіқұрастырып жасағанда, ол жағадан аттанарда немесе жағаға келіп токтағанда оны материялық нүкте деп есептей алмаймыз. Сол сияқты күн мен түннің немесе жылмезгілдерінің ауысу себептерін қарастырғанда, Жердің өлшемдері мен пішінін ескермеуге болмайды.

Тағы бір мынадай қарапайым мысал келтірейік. Мектептен шыққан оқушы үйіне дейін 1 км ара кашықтыкты жүріп өтсін. Бұл жағдайда баланың қозғалысын қарастырғанда оны материялық нүкте деп есептеуге болады. Өйткені, баланың өлшемдері ол жүріп өткен қашыктықпен салыстырғанда тым аз. Ал енді сол бала таңертеңгілік дене шынықтыру жаттығуларын жасап жатқанда оны материялық нүкте ретінде қарастыра алмаймыз. Бұдан бір ғана денені кей жағдайда материялық нүкте есебінде қарастыруға болса, ал кейбір жағдайда оны материялық нүкте ретінде қарастыруға болмайтыны байқалады. Қандай да бір козгалысты қарастырганда қайсыбір денені материялық нүкте ретінде қарастыру не карастырмау, сол дененің өзіне емес,көбінесе, қозғалыстың сипатына, жауабы ізделініп отырған сұрактың мазмұнына байланысты. Егер дененің нақты өлшемі мәселені шешуде басты рөл аткармайтын болса, онда оны материялық нүкте деп қарастыруға болады. Ал дененің салыстырмалы өлшемі қарастырылып отырған қозғалыста маңызды орын алатын болса, онда денені материялық нүкте ретінде карастыруға болмайды.

Енді қозғалыс траекториясы деген не, соған тоқталайық. Жолаушы Алматыдан Астанаға дейін ұшақпен немесе поезбен сапар шегеді делік. Бұл кезде ұшақ пен поездың шын мәнінде қозғалған сызықтары бір-бірімен беттеспейді. Олай дейтініміз, ұшақ біршама түзу сызық сызып, төтесінен ұшатын болса, поезд жол-жәнекей басқа қалаларға да тоқтап, қисық сызық бойымен жүреді. Дененің немесе материялық нүктенің санақ денесімен салыстырғандағы қозғалысы кезінде сызық түрінде қалдырған ізі қозғалыс траекториясы деп аталады.

Біз қарастырған мысалдардағы поезд жүретін темір жол - поездың, тас жол (шоссе) - автомобильдердің, ұшақтың артында қалған тұманды із - ұшақтың, соқпақ жол - жаяу адамның қозғалыс траекториясын көрсетеді. Сол сияқты қозғалыс траекториясының да пішіні әртүрлі санақ денесіне катысты түрліше болады. Траекторияның түріне қарап қозғалысты тузусызықты немесе қисықсызықты (мысалы, шеңбер бойымен, парабола бойымен жәнө т. с.с.) деп бөледі.^[2]

Механика [грек. ''mechanіke'' (techne) – машина және машина жасау өнері] – материалдық денелердің механикалық қозғалысын және өзара әсерлесуін зерттейтін ғылым. Денелердің немесе олардың бөлшектерінің уақыттың өтуіне байланысты кеңістіктегі орындарының өзгеруі механикалық қозғалыс деп аталады. Табиғатта мұндай қозғалысқа аспан әлеміндегі денелердің қозғалысы,Жер қыртысының тербелуі, мұхит-теңіздер мен ауадағы ағындар тербелісі; техникада – ұшу аппараттарының, көлік құралдарының, әр алуан механизм бөліктерінің қозғалысы, ғимараттар элементтерінің деформациясы, сұйықтықтар мен газдардың қозғалыстары, т.б. жатады. Әдетте, Механика деп Ньютонның механикалық заңдарына негізделген жарық жылдамдығынан әлдеқайда төмен жылдамдықпен қозғалатын кез келген материалдық денелердің қозғалысын сипаттайтын (элементар бөлшектерден басқа)классикалық механиканы айтады. Механикада материалдық денелердің қозғалысын зерттегенде олардың негізгі қасиеттерін сипаттайтын абстракты ұғымдар пайдаланылады:

1. материалдық нүкте – массасы бар, геометриялық өлшемдері ескерілмейтін дене;

2. абсолют қатты дене – кез келген екі нүктесінің ара қашықтығы барлық жағдайда тұрақты дене;

3. өзгермелі тұтас орта – қатты денелердің, сұйықтықтар мен газдардың қозғалысын зерттегенде олардың молекулалық құрылымын ескермеуге болатын жағдайда қолданылатын ұғым.

6. инерциалдық санақ жүйесі – еркін материалдық нүкте бірқалыпты және түзу сызықты қозғалатын жүйе

инерциалдық емес санақ жүйесі – инерциалдық жүйеге қатысты үдеумен қозғалатын санақ жүйесі, мүнда Ньютон заңы да, импульстың сақтау заңы да, инерция заңы да , импульстың сақталу заңы да орындалмайды

Инерциалды санақ жүйелері.. Қозғалмайтын жұлдыздар сферасына қатысты бірқалыпты ілгерлемелі түзу сызықты қозғалатын барлы санақ жүйелерінде механикалық құбылыстар бірдей өтеді.

Ауырлық өрісі өте аз деп есептелік. Осындай санақ жүйелерінде Ньютон заңдары орындалады және олар инециялдық санақ жүйелері деп аталады.

Галилей ең алғаш рет ұсынған барлық инерциялды санақ жүйелерінде механикалық құбылыстар бірдей өтеді деген тұжырым, Галилейдің салыстырмалық принципі деп аталады.

Қатты дененің ең қарапайым қозғалысы, оның бірқалыпты түзу сызықты ілгерлемелі қозғалысы болып табылады. Қатты дененің қарапайым қозғалысыда бірқалыпты түзусызықты ілгерлемелі қозғалысы болады. Санақ жүйелерінің біреуін шартты түрде қозғалмайтын, ал екіншісін қозғалатын деп аламыз. Әрбір санақ жүйесіне декарттық координат жүйесін енгіземіз. Қозғалмаайтын К санақ жүйесіндегі координанттарды (x, y, z), ал қозғалатын K' санақ жүйесіндегі координаттарды (x', y', z') деп белгілейік. K' жүйесі К жүйесіне қатысты жылдамдықпен қозғалсын делік.

Қазғалатын санақ жүйесі қозғалмайтын санақ жүйесіне қатысты әрбір уақыт мезетінде белгілі бір орынға ие болады.

Сурет 2.1

x, y, z координаталары x', y', z' кординаталымен қайсы бір Р ушін мыныдай байланыста болады:

x’ = x – vt, y’ = y, z’ = z, t’ = t (2.9).

Осы формулалар Галилей түрлендірулері деп аталады.

 7.  ньютонның бірінші заңы: кез келген дене (материалдық нүкте) өзінің тыныштық күйін немесе бірқалыпты және түзу сызықты қозғалысын басқа денелер әсер еткенге дейін сақтайды. 

   бұл заң тек  инерциялық санақ жүйесінде  ғана орындалады, яғни инерциялық санақ жүйесінің бар болуы туралы тұжырым  ньютонның бірінші заңын айқындайды.

   ньютонның екінші заңы: дененің (материалдық нүктенің) алған үдеуі әсер етуші күшке тура пропорционал және бағыттас, дененің (материалдық нүктенің) массасына кері пропорционал болады.

.                                                    (1)

осы өрнекті нүкте импульсі анықтамасына сәйкес (18) түрлендіргенде

.                                  (2)

    дене импульсінің уақытқа қатысты бірінші туындысы оған әсер етуші күшке тең. (2) формула  ілгерілемелі қозғалыстың динамикалық теңдеуі деп аталады.соңғы формуланы мына түрде жазғанда:

,

мұндағы  - әсер етуші күштің импульсі,  -дене импульсінің өсімшесі. осыдан:

әсер етуші күштің импульсі дене импульсінің өзгерісіне тең.

        

  ньютонның үшінші заңы: өзара әрекеттесетін екі нүктенің бір-біріне әсер күші шама жағынан тең, бағыттары қарама-қарсы болады:                                             

   .                                                  (3)

   біртұтас дене болып есептелетін материалдық нүктелер жиынтығын механикалық жүйе деп атайды. жүйенің материалдық нүктелерінің бір-бірімен өзара әсерлесу күші ішкі күштер деп, ал жүйенің материалдық нүктелеріне сыртқы денелердің әсер ету күші сыртқы күштер деп аталады. сыртқы күштер әсер етпейтін денелердің механикалық жүйесі  тұйық немесе оқшауланған жүйе болып есептеледі.

     массалары        және  сәйкесінше  жылдамдықтары            денелердің механикалық жүйеде   - де нелердің әрқайсына әсер ететін сыртқы тең әсерлі күштер, ал    - осы денелердің әр денесі үшін ньютонның екінші заңына сәйкес жүйенің әр денесі үшін:

,           ,      ....,       .

осы теңдеулерді мүшелеп қосқанда:     

      .             (4)

ньютонның үшінші заңына сәйкес механикалық жүйенің ішкі күштерінің геометриялық қосындысы нөлге тең болатындықтан:

, немесе   , (5)

мұндағы    - жүйенің толық импульсі.

Масса. Ээксперимент нәтижелері үдеудің бағыты күш бағытымен бағыттас екенін көрсетеді.Бір күш әртурлі денелерге әртүрлі үдеу береді.. Әртүрлі күштер бір денеге әртүрлі үдеу береді.. Бірақ күштің удеуге қатынасы бір ғана шамаға тең.

. (2.2)

Егер (2.2) қатынасын векторлық түрде жазатын болсақ, онда (2.1) өрнегі шығады. Бұл теңдеуді басқа түрде жазуға болады:

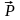, = . (2.3)

Массаның жылдамдыққы көбейтіндісі = импульс деп аталады.

Денеге әсер еткен күштің удеуге қатынасмен анықталатын дененің қасиеті инерттілік деп аталады. Ал инерттілікті сипаттайтын шама масса болып табылады.

8. импульс моменті, "Қозғалыс мөлшері моменті" деп те аталады, – материалдық нүктенің немесе жүйенің механикалық қозғалысының динамикалық сипаттамаларының бірі. Физикада ол заттың бастапқы нүктеден қозғалу мен ауысуының физикалық шамасы болып өрнектеледі.

 Күш моменті тәрізді қозғалыс мөлшерінің моменті центрге (нүктеге) және оське де қатысты анықталады.

Материалдық нүктенің центрге (O) қатысты қозғалыс мөлшерінің моменті центрден жүргізілген қозғалыстағы нүктенің радиус-векторының (r) оның қозғалыс мөлшерінің (mυ) векторлық көбейтіндісіне тең: яғни

K₀=[r.mυ].

Оны есептеу үшін күш моментін есептеуге арналған барлық формулаларды пайдалануға болады, тек онда F векторын (немесе оның проекцияларын) mυ векторымен (немесе оның проекцияларымен) алмастыру қажет.

Қозғалыс мөлшерінің моментінің өзгерісі түсірілген күштің m0(F) моментінің әсерінен болады. Бұл өзгерістің сипаты динамиканың негізгі заңы болып табылатын =m₀F теңдеуімен анықталады.

m₀F=0 болған кезде, мысалы, центрлік күштер үшін орындалады, нүктенің O центрге қатысты қозғалыс мөлшерінің моменті өзгеріссіз қалады; нүкте осы кезде жазық қисық бойымен қозғалады және оның радиус-векторы кез келген бірдей уақыт аралықтарында бірдей аудандар сызып өтеді. Бұл нәтиже аспан механикасы үшін, сонымен қатар ғарыш ракеталарының, жердің жасанды серіктері, т.б. қозғалысы үшін маңызды.

Импульс моментінің сақталу заңы- тұйықталған жүйенің импульс моменті жүйе ішінде өтетін кез-келген прцестер кезінде өзгермейді.

Кей жағдайда, жүйе толығымен тұйықталмаған болса, онда сыртқы күштердің проекциясы нөлге тең болатын бағытта импульс моментінің проекциясы тұрақты болады:

L_z=const.

Монымен тұйықталған жүйенің импульс моменті тұрақты болып қалады. Ол үшін сыртқы куштердің қорытқы моменті нөлге тең болуы керек

Импульс моменті және оның сақталу заңы

Массасы   қатты дененің кішкентай бөлшегін қарастырайық. Оның жылдамдығы   және оған қатысты импульсі   нүкте траекториясына жанама бойымен бағытталған.

1-сурет.Импульс моментін анықтау

Қозғалмайтын О нүктесіне қатысты импульс моменті векторы   материялық нүктенің радиус-векторы   мен оның импульсінің   векторлық көбейтіндісіне тең физикалық шама: . Импульс моменті векторы  векторлық көбейтінді ережесі арқылы анықталып, айналу осі бойында жатады, ал оның модулі мына өрнекпен анықталады: