Задание 5

Вероятность «сбоя» в работе телефонной станции при каждом вызове равна р=0,004. Определить вероятность того, что:

а) из поступивших 9 вызовов ровно пять «сбоев»;

б) число «сбоев» m удовлетворяет неравенству .

Решение

а) Условие задачи можно рассматривать как серию из n=9 независимых испытаний, состоящих в проверке вызовов на сбой, в каждом из которых с вероятностью p=0,004 может осуществиться событие {при вызове произойдет «сбой»}. Вероятность того, что «сбоя» не будет, равна q=1–p=1–0,004=0,996.

Для вычисления вероятностей того, что в n испытаниях событие наступит m раз, воспользуемся формулой Бернулли:

Таким образом, искомое событие практически невозможно.

б) Вероятность того, что событие появится не менее k₁ и не более k₂ раз находится по интегральной теореме Муавра-Лапласа:

, где

.

В нашем случае

Тогда

.

Таким образом, искомое событие практически невозможно.

Ответ: а)  событие практически невозможно; б) событие практически невозможно.

Задание 6

Случайная величина Х равномерно распределена в интервале (-2;4).

Требуется найти:

1) дифференциальную (плотность вероятности) и интегральную функцию распределения случайной величины Х;

2) найти математическое ожидание, дисперсию и среднеквадратическое отклонение;

3) найти вероятность попадания случайной величины в интервал (-1;2).

Решение

1) Плотность вероятности непрерывной случайной величины, равномерно распределенной в интервале (a,b), имеет вид:

В нашем случае а=-2, b=4, поэтому функция плотности будет

Интегральная функция распределения имеет вид:

2) Находим числовые характеристики случайной величины, которая распределена по равномерному закону.

Математическое ожидание:

.

Дисперсия:

.

Среднее квадратическое отклонение:

.

3) Для нахождения искомой вероятности воспользуемся формулой:

.

Получим

.

Ответ: 1)  ; ;

2) ; ; ; 3)  .

Задание 7

Случайная величина X задана функцией распределения:

Требуется:

1. найти дифференциальную функцию (плотность вероятности);

2. найти математическое ожидание и дисперсию X;

3. построить графики интегральной и дифференциальной функций;

4. найти вероятность попадания случайной величины Х в интервал (1;3).

Решение

1) Находим плотность распределения вероятностей по формуле

f(x)=F^/(x).

Получим

2) Находим математическое ожидание непрерывной случайной величины Х:

.

Дисперсия равна

3) Построим графики функций F(x) и f(x).

4) Искомую вероятность находим по формуле

.

Тогда

.

Ответ: 1)  ; 2)  ; ;

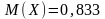3) графики на рисунках; 4) .

Задание 8

Применяя неравенство Чебышева, оцените вероятность того, что случайная величина Х отклонится от своего математического ожидания менее чем на 4σ, где .

Решение

Справедливо неравенство Чебышева:

Вероятность того, что отклонение СВ Х от ее математического ожидания по абсолютной величине меньше положительного числа ε, не меньше чем , т.е.

, где σ²=D(X) – дисперсия СВ.

В нашем случае:

.

Значит, искомая вероятность не менее 0,9375.

Ответ: искомая вероятность не менее 0,9375.