Государственное образовательное учреждение высшего профессионального образования

«Самарский государственный аэрокосмический университет

им. академика С.П.Королёва»

Однофакторный дисперсионный анализ технологических процессов

Самара, 2008

Составители: Б.Н. Березков, А.В. Архипов

УДК

Однофакторный дисперсионный анализ технологических процессов: Метод. указания к лаб. раб./ Сост. Б.Н.Березков, А.В. Архипов. - Самара: Изд-во Самар.гос.аэрокосм. ун-та,2008.

Цель работы: знакомство с методами дисперсионного анализа технологических процессов.

1. Теоретические основы однофакторного дисперсионного анализа.

Усложнение РЭС и технологических процессов их производства вызывает резкое повышение стоимости и длительности экспериментальных исследований, усложнение экспериментальных установок и увеличение сроков обработки результатов. Поэтому существует необходимость в совершенствовании методологии исследования, в разработке способов обработки экспериментальных данных.

Одним из первых шагов в этом направлении был однофакторный дисперсионный анализ, разработанный и введенный в практику выдающимся английским математиком-статистиком Р.А.Фишером.

Таблица 1. Результаты наблюдений

Номер уровня фактора А	Номер испытания 1 2…j…n	Суммы	Число испытаний
1	x11 x12…x1j…x1m	S1	n
2	x21 x22…x2j…x2m	S2	n
…	… … … …		…	…
i	xi1 xi2…xij…xim	Si	n
…	… … … …	…	…	…
m	xm1xm2…xmj…xmm	Sm	n
		S…	N=m·n

Примечание: точка вместо индекса у сумм указывает на суммирование по данному индексу.

Сущность однофакторного дисперсионного анализа заключается в разложении суммарной (общей) дисперсии на две составляющие: дисперсию, обусловленную действием изучаемого фактора А, и дисперсию с ошибкой эксперимента. При этом производится сравнение оценки дисперсии, вызванной изучаемым фактором А и оценки дисперсии ошибки эксперимента.

Для выполнения дисперсионного анализа результаты наблюдений и расчетов удобно сводить в таблицу 1.

Несмещенные оценки для дисперсии получим, разделив суммы квадратов на соответствующее число степеней свободы:

; (1)

; (2)

. (3)

К формулам (1), (2) и (3) относятся числа степеней свободы N-1, m-1, N-m соответственно, где N=m·n.

При этом сами суммы квадратов после преобразований и упрощений определяются выражениями:

; (4)

; (5)

. (6)

Расхождение между и оценивается обычно с помощью F – критерия Фишера:

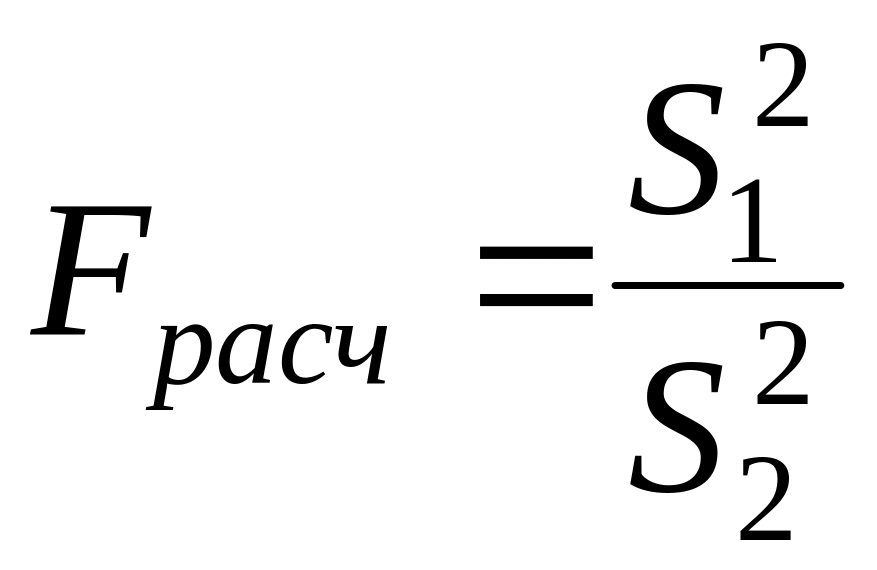. (7)

сравнивается с табличным значением (Приложение А). Если , определенного для выбранной доверительной вероятности (надежности вывода) Р и числа степеней свободы , , то расхождение дисперсий считают неслучайным (значимым) и изученный фактор А оказывает влияние на исследуемый выходной параметр. В противном случае для такого утверждения нет достаточных оснований.

Доверительную вероятность обычно выбирают P=0,95 или P=0,99. Соответственно, уровень значимости q=0,05 или q=0,01.

Иногда для упрощения расчетов при дисперсионном анализе переходят на так называемые кодированные величины. Закодировать – это значит прибавить (или вычесть) ко всем случайным числам одно и то же число или умножить все случайные числа на одно и то же число. Например, вместо чисел 50, 64, 45, 43, вычитая из каждого показания число 50, получим кодированные числа 0, 14, -5, -8. Результаты расчетов при этом не изменятся.