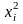Контрольная работа по эконометрике
Вариант 10.
Задание 1.
По данным изменения социологического процесса построить математическую модель, используя интерполяционную формулу Лагранжа. Сделать прогноз по процессу в 2012 году.
Годы |
Показатель |
2002 |
65 |
2005 |
70 |
2008 |
75 |
2011 |
77 |
Решение.
Введем обозначения. Через X обозначим столбец, в котором приведены независимые данные, т.е. «Годы». Через Y – столбец с зависимыми данными, т.е. «Показатель».
Кроме того, для удобства ведения расчета упростим значения столбца X. Через 2 обозначим первое значение (2002 год), соответственно 2005 год – 5 и т.д. Тогда математическая таблица пример вид:
X |
Y |
2 |
65 |
5 |
70 |
8 |
75 |
11 |
77 |
Построение математическую модель, с использование формулы Лагранжа.
При интерполяции с помощью формулы Лагранжа, для n=3 имеем:
Тогда
Преобразовав
данное выражение, раскрывая скобки и,
приводя слагаемые к общему знаменателю,
получим:
-
интерполирующая функция.
Определим
значение
при
:
.
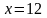Задание 2.
Экспериментально
получены пять значений функции
при пяти значениях аргумента, которые
записаны в таблице:
|
1 |
2 |
3 |
4 |
5 |
|
5,9 |
6,9 |
5,4 |
3,4 |
3,9 |
Методом
наименьших квадратов найти функцию
вида
,
выражающую приближенно (аппроксимирующую)
функцию
.
Сделать чертеж, на котором в декартовой прямоугольной системе координат построить экспериментальные точки и график аппроксимирующей функции .
Решение.
Найдем параметры уравнения методом наименьших квадратов. Используем формулы:
Составим вспомогательную таблицу:
i |
|
|
|
|
1 |
1 |
5,9 |
1 |
5,9 |
2 |
2 |
6,9 |
4 |
13,8 |
3 |
3 |
5,4 |
9 |
16,2 |
4 |
4 |
3,4 |
16 |
13,6 |
5 |
5 |
3,9 |
25 |
19,5 |
|
15 |
25,5 |
55 |
69 |
Тогда, подставляя в систему, полученные в таблице данные, получим:
Откуда, выражая из первого уравнения а и, подставляя его во второе уравнение получим:
Тогда искомая функция имеет следующий вид:
Сделаем чертеж, на котором в декартовой прямоугольной системе координат построим экспериментальные точки и график аппроксимирующей функции
Задание 3.
Имеются
три пункта поставки однородного груза
пять пунктов
потребления этого груза. На пунктах
находится груз соответственно в
количестве 200, 350, 300 т. В пункты
требуется доставить соответственно
270, 130, 190, 150, 110 т груза.
Расстояние между пунктами потребления приведено в следующей матрице таблице:
Пункты поставки |
Пункты потребления |
||||
|
270 |
130 |
190 |
150 |
110 |
200 |
24 |
50 |
55 |
27 |
16 |
350 |
50 |
47 |
23 |
17 |
21 |
300 |
35 |
59 |
55 |
27 |
41 |
Найти план перевозок данной транспортной задачи методом северо-западного угла.