
- •Содержание
- •Часть I «Дифференциальное исчисление функций»
- •Часть II
- •Основные теоретические сведения для выполнения заданий 1-4
- •Приложения производной к задачам геометрии.
- •Полное исследование функций и построение графика.
- •Функции нескольких переменных и их дифференцирование.
- •Полный дифференциал функции двух переменных и его применение в приближенных вычислениях.
- •1. Сделать разложение функции по формуле Тейлора при указанном значении :
- •2.. Составить уравнение касательной и нормали к кривой в точке .
- •4. Дана функция и точка . С помощью дифференциала вычислить приближенное значение функции в данной точке..
- •1. Неопределенный интеграл.
- •2. Формулы интегрирования и таблица основных интегралов.
- •3. Интегрирование методом подстановки или замены переменной.
- •4. Интегрирование по частям.
- •5. Интегрирование рациональных дробей.
- •6. Интегрирование иррациональных выражений.
- •7. Интегрирование тригонометрических функций.
- •8. Определенный интеграл.
- •9. Несобственные интегралы. Интегралы с бесконечными пределами
- •10. Приложения определенного интеграла.
- •11. Двойной интеграл.
- •12. Тройной интеграл.
- •1. Дифференциальные уравнения первого порядка. Уравнения с разделяющимися переменными
- •Линейные уравнения первого порядка
- •Однородные уравнения
- •Определение типа дифференциального уравнения первого порядка
- •Понижение порядка дифференциального уравнения
- •Пример 5. Решить уравнение .
- •Системы дифференциальных уравнений
- •2. Линейные дифференциальные уравнения высшего порядка с постоянными коэффициентами
- •Общее решение однородного линейного дифференциального уравнения с постоянными коэффициентами
- •Общее решение неоднородного линейного дифференциального уравнения с постоянными коэффициентами
- •1. Числовые ряды.
- •Ряды с положительными членами
- •Пусть даны два ряда с положительными членами
- •Ряды с произвольными членами
- •2. Степенные ряды.
- •Ряд Тейлора
- •Разложение основных элементарных функций в ряд Маклорена
- •Интегрирование дифференциальных уравнений с помощью рядов
- •3. Ряд Фурье.
- •1. Вычислить неопределенные интегралы:
- •2. Вычислить несобственные интегралы или доказать их расходимость.
- •3.Вычислить объем тела, полученного вращением кривых и вокруг оси .
- •5. С помощью тройного интеграла вычислить объем тела, ограниченного заданными поверхностями. Сделать рисунки областей и .
- •7. Для данного дифференциального уравнения второго порядка найти частное решение, удовлетворяющее заданным начальным условиям: , , .
- •9. Разложить в ряд Фурье функцию на отрезке .
- •Литература.
Индивидуальное задание
по дисциплине «Основы высшей математики»
для студентов очной формы обучения
(3 семестр)
Содержание
Задания 1-4 (часть 1)………………………………………………3-6
Задания 1-9 (часть2)……………………………………………….6-18
Основные теоретические сведения (часть1)……………...……..19-28
Решение 0-варианта (часть 1)…………………….…………...….29-30
Основные теоретические сведения (часть2)........…………...…..31-60
Решение 0-варианта (часть2)……………………….…………….61-71
Литература………………………………………………….………..72
_________________________________________________________________________
Часть I «Дифференциальное исчисление функций»
Задание 1. Сделать разложение функции по формуле Тейлора при указанном значении x=x0.
1.![]() .
.
2.
![]() .
.
3.
![]() .
.
4.
![]() .
.
5.
![]() .
.
6.
![]() .
.
7.
![]() .
.
8.
![]() .
.
9.
![]() .
.
10.
![]() .
.
11. .
12. .
13. .
14. .
15. .
16. .
17. .
18. .
19. .
20. .
21. .
22. .
23. .
24. .
25.
Задание
2.
Составить уравнение касательной и
нормали к кривой
![]() в точке А.
в точке А.
1.
![]() ;
A(0,7), 2.
;
A(0,7), 2.
![]() ;
A(1;-4);
;
A(1;-4);
3.
![]() ;
A(0;4), 4.
;
A(0;4), 4.
![]() ;
A(1;5);
;
A(1;5);
5.
![]() ;
A(1;3), 6.
;
A(1;3), 6.
![]() ;
A(2;-3);
;
A(2;-3);
7.
![]() ;
A(/8;4); 8.
;
A(/8;4); 8.
![]() ;
A(1;1);
;
A(1;1);
9.
![]() ;
A(0;4); 10.
;
A(0;4); 10.
![]() ;
A(2;10).
;
A(2;10).
11. ; A(0,7), 12. ; A(1;-4);
13. ; A(0;4), 14. ; A(1;5);
15. ; A(1;3), 16. ; A(2;-3);
17. ; A(/8;4); 18. ; A(1;1);
19. ; A(0;4); 20. ; A(2;10).
21. ; A(0,7), 22. ; A(1;-4);
23. ; A(0;4), 24. ; A(1;5);
25. ; A(1;3),
Задание
3.
Дана функция
![]() .
Показать,
что
.
Показать,
что
![]() .
.
1.
![]() ;
;
![]() ;
;
2.
![]() ;
;
![]() ;
;
3.
![]() ;
;
![]() ;
;
4.
![]() ;
;
![]() ;
;
5.
![]()
![]() ;
;
6.
![]() ;
;
![]() ;
;
7.
![]() ;
;
![]() ;
;
8.
![]() ;
;
![]() ;
;
9.
![]() ;
;
![]() ;
;
10.![]() ;
;
![]() .
.
11. ; ;
12. ; ;
13. ; ;
14. ; ;
15. ;
16. ; ;
17. ; ;
18. ; ;
19. ; ;
20. ;
21. ; ;
22. ; ;
23. ; ;
24. ; ;
25. .
Задание 4. Дана функция и точка M0(x0;y0). С помощью дифференциала вычислить приближенное значение функции в данной точке.
1.
![]() ; M0(1,08;1,94);
; M0(1,08;1,94);
2.
![]() ; M0(3,04;3,95);
; M0(3,04;3,95);
3.
![]() ; M0(2,98;2.05);
; M0(2,98;2.05);
4.
![]() ; M0(1,06;2,92);
; M0(1,06;2,92);
5.
![]() ; M0(2,94;1,07);
; M0(2,94;1,07);
6.
![]() ; M0(1,96;1,04);
; M0(1,96;1,04);
7.
![]() ; M0(0,96;1,95);
; M0(0,96;1,95);
8.
![]() ; M0(3,96;1,03);
; M0(3,96;1,03);
9.
![]() ; M0(0,97;2,03);
; M0(0,97;2,03);
10.
![]() ; M0(2,98;3,91).
; M0(2,98;3,91).
11. ; M0(1,08;1,94);
12. ; M0(3,04;3,95);
13. ; M0(2,98;2.05);
14. ; M0(1,06;2,92);
15. ; M0(2,94;1,07);
16. ; M0(1,96;1,04);
17. ; M0(0,96;1,95);
18. ; M0(3,96;1,03);
19. ; M0(0,97;2,03);
20. ; M0(2,98;3,91).
21. ; M0(1,08;1,94);
22. ; M0(3,04;3,95);
23. ; M0(2,98;2.05);
24. ; M0(1,06;2,92);
25. ; M0(2,94;1,07);
__________________________________________________________________________
Часть II
«Интегральное исчисление функций. Дифференциальные уравнения. Ряды»
Задание 1 . Вычислить неопределенные интегралы.
1. а)
![]() ,б)
,б)![]() , в)
, в)![]() , г)
, г)![]() , д)
, д)![]() .
.
2. а)![]() ,б)
,б)![]() ,в)
,в)![]() , г)
, г)![]() , д)
, д)![]() .
.
3. а)![]() , б)
, б)![]() , в)
, в)![]() , г)
, г)![]() , д)
, д)![]() .
.
4. а)![]() , б)
, б)![]() ,
в)
,
в)![]() , г)
, г)![]() , д)
, д)![]() .
.
5. а)![]() , б)
, б)![]() , в)
, в)![]() , г)
, г)![]() , д)
, д)
![]() .
.
6. а)![]() ,
б)
,
б)![]() , в)
, в)![]() , г)
, г)![]() , д)
, д)![]() .
.
7. а)![]() ,
б)
,
б)![]() ,в)
,в)![]() ,
г)
,
г)![]() , д)
, д)![]() .
.
8. а)![]() , б)
, б)![]() , в)
, в)![]() , г)
, г)![]() , д)
, д)![]() .
.
9. а)![]() ,
б)
,
б)![]() ,
в)
,
в)![]() , г)
, г)![]() , д)
, д)![]() .
.
10.а)![]() , б)
, б)![]() , в)
, в)![]() , г)
, г)![]() , д)
, д)![]() .
.
11.а) , б) , в) , г) , д) .
12.а) , б) , в) , г) , д) .
13.а) , б) , в) , г) , д) .
14.а) , б) , в) , г) , д) .
15.а) , б) , в) , г) , д) .
16.а) , б) , в) , г) , д) .
17.а) , б) , в) г) , д) .
18.а) , б) , в) , г) , д) .
19.а) , б) , в) , г) , д) .
20.а) , б) , в) , г) , д) .
21.а) , б) , в) , г) , д) .
22.а) , б) , в) , г) , д) .
23.а) , б) , в) , г) , д) .
24. а) ,б) , в) , г) , д) .
25.а) , б) , в) , г) , д) .
Задание 2. Вычислить несобственные интегралы или доказать их расходимость.
1.
![]()
2.![]()
3.![]()
4.![]()
5.![]()
6.![]()
7.![]()
8.![]()
9.![]()
10.![]()
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
Задание 3
1. Вычислить площадь
фигуры, ограниченной одной аркой циклоиды
![]() и осью
и осью
![]()
2. Вычислить длину
дуги кубической параболы
![]() от точки (-1;-1) до точки (2;8).
от точки (-1;-1) до точки (2;8).
3. Вычислить площадь
поверхности вращения линии
![]() вокруг оси
вокруг оси
![]() для
для
![]() [0;2].
[0;2].
4. Вычислить объем
тела, образованного вращением линии
![]() вокруг оси
для
вокруг оси
для
![]() [-1;1]
[-1;1]
5. Вычислить площадь
фигуры, ограниченной кардиоидой
![]()
6. Вычислить длину
дуги астроиды
![]()
![]()
![]() [0;
[0;![]() ].
].
7. Вычислить площадь
поверхности, образованной вращением
дуги астроиды
![]() вокруг оси
вокруг оси
8. Вычислить объем
тела, полученного вращением линий
![]() и
вокруг оси
и
вокруг оси
![]()
9. Вычислить длину
кардиоиды
![]()
10. Вычислить площадь
фигуры, ограниченной одной аркой циклоиды
![]() и осью
и осью
11. Вычислить площадь фигуры, ограниченной одной аркой циклоиды и осью
12. Вычислить длину дуги кубической параболы от точки (-1;-1) до точки (2;8).
13. Вычислить площадь поверхности вращения линии вокруг оси для [0;2].
14. Вычислить объем тела, образованного вращением линии вокруг оси для [-1;1]
15. Вычислить площадь фигуры, ограниченной кардиоидой
16. Вычислить длину дуги астроиды [0; ].
17. Вычислить площадь поверхности, образованной вращением дуги астроиды вокруг оси
18. Вычислить объем тела, полученного вращением линий и вокруг оси
19. Вычислить длину кардиоиды
20. Вычислить площадь фигуры, ограниченной одной аркой циклоиды и осью
21. Вычислить площадь фигуры, ограниченной одной аркой циклоиды и осью
22. Вычислить длину дуги кубической параболы от точки (-1;-1) до точки (2;8).
23. Вычислить площадь поверхности вращения линии вокруг оси для [0;2].
24. Вычислить объем тела, образованного вращением линии вокруг оси для [-1;1]
25. Вычислить площадь фигуры, ограниченной кардиоидой
Задание. 4. В области D, ограниченной заданными линиями, вычислить двойной интеграл. Сделать рисунок.
1.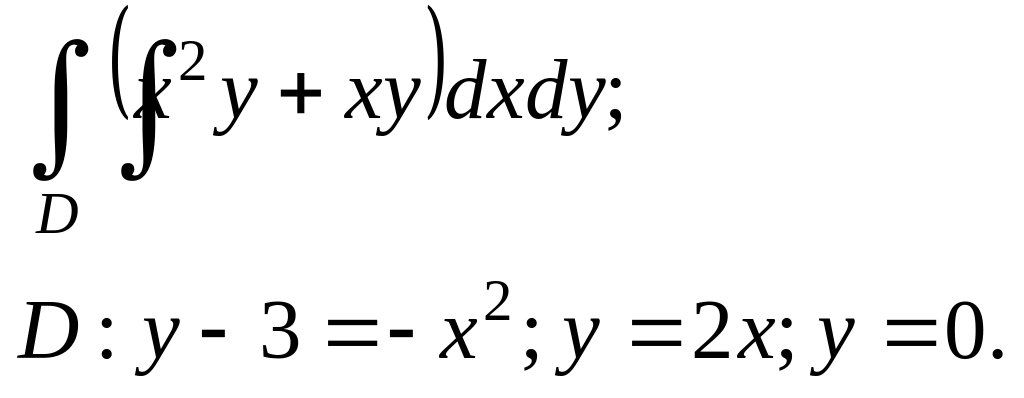
2.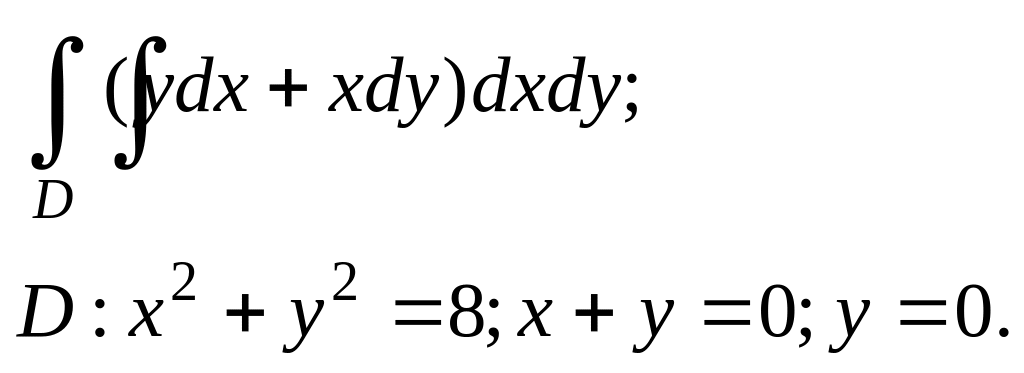
3.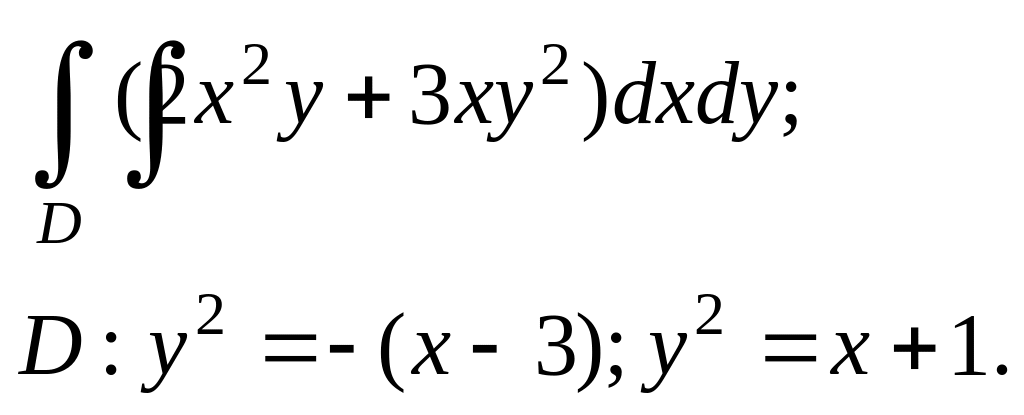
4.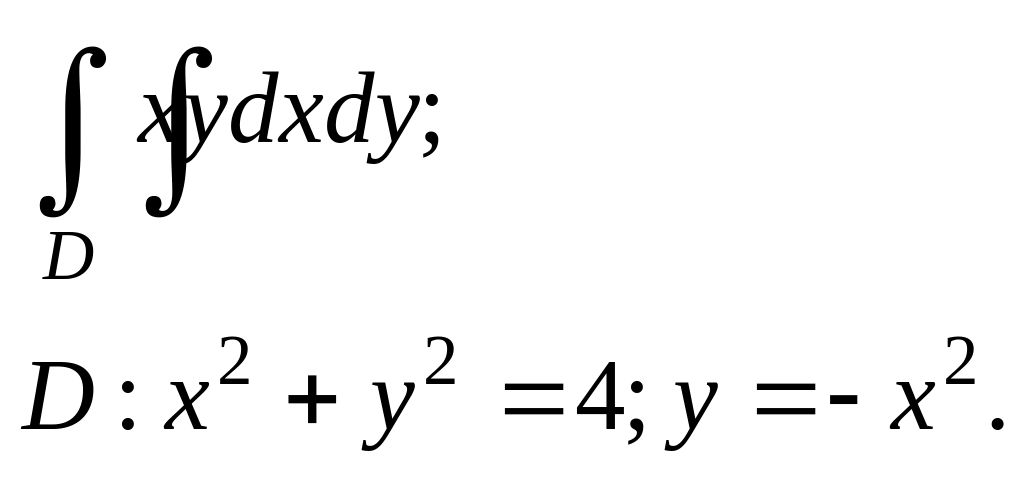
5.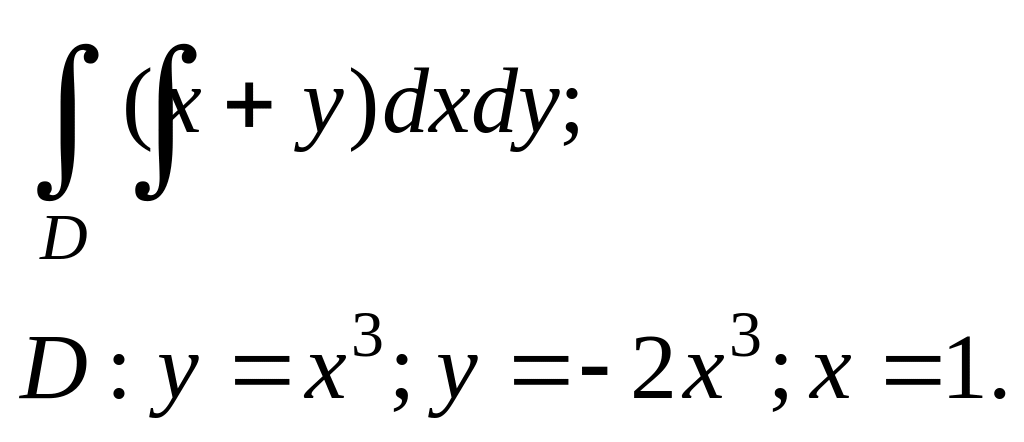
6.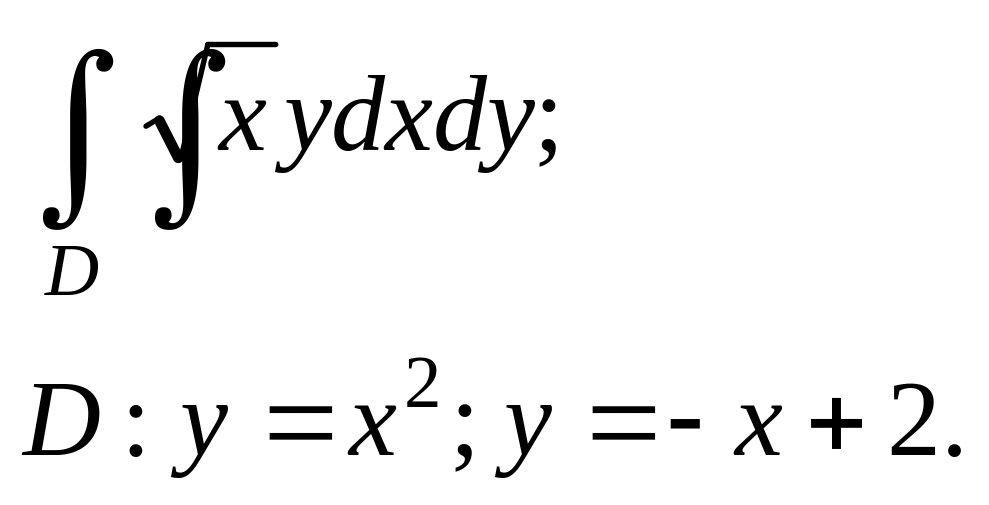
7.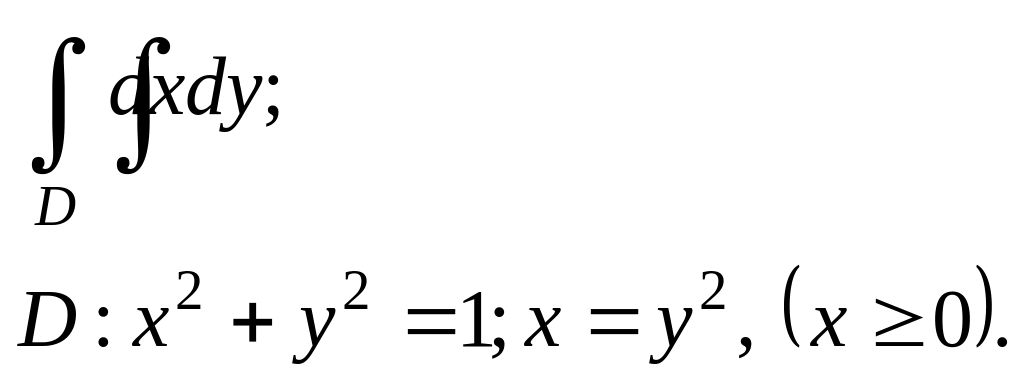
8.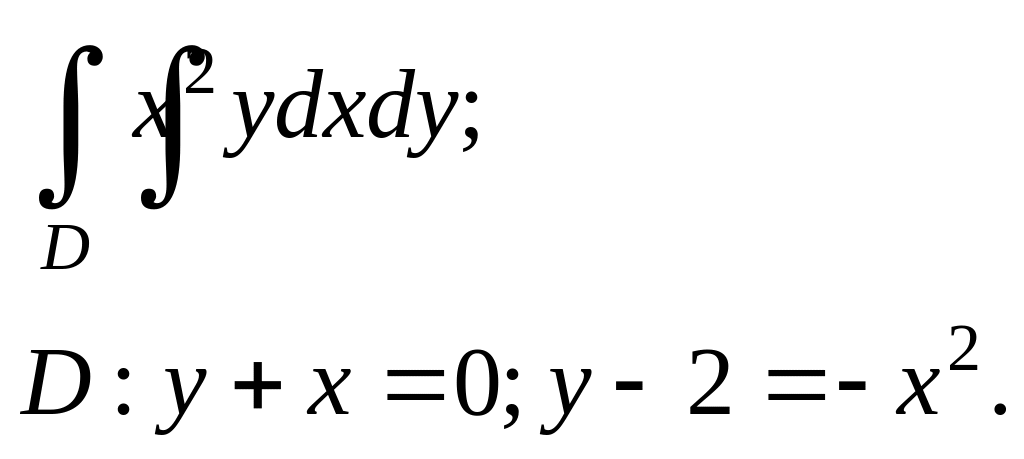
9.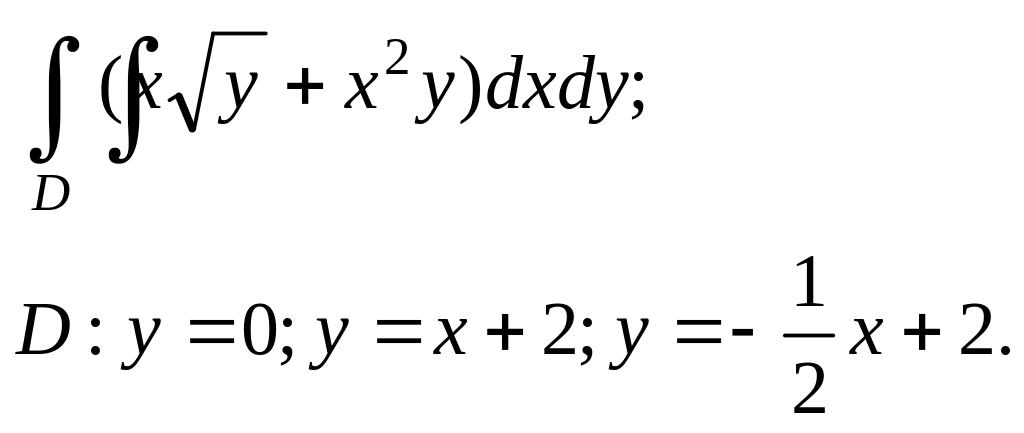
10.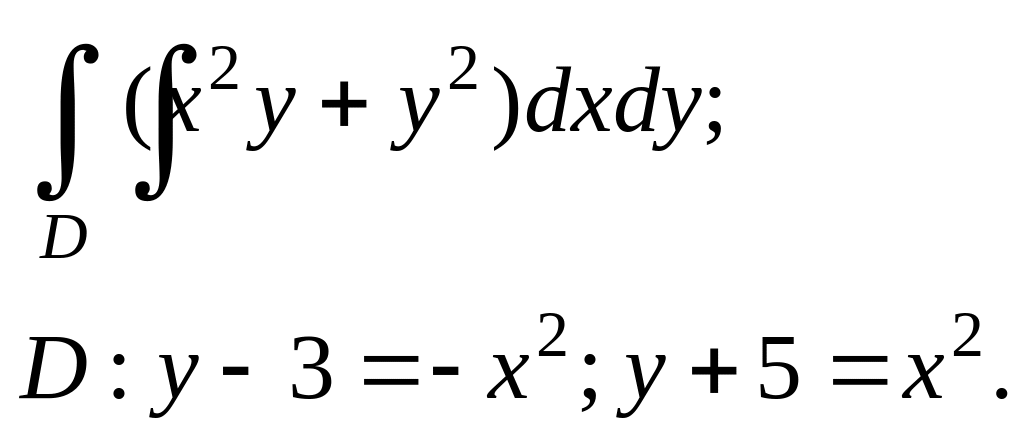
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
Задание
5. С
помощью тройного интеграла вычислить
объем тела, ограниченного заданными
поверхностями. Сделать рисунки областей
V
и D
(![]() - проекция
области
- проекция
области
![]() на
плоскость
на
плоскость
![]() ).
).
.
Плоскостями координат, плоскостями х=2, у=3 и эллиптическим параболоидом
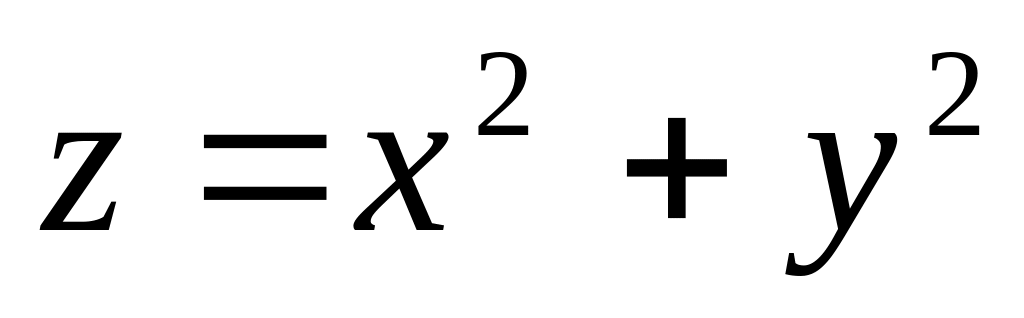 .(отв
11)
.(отв
11)Плоскостью
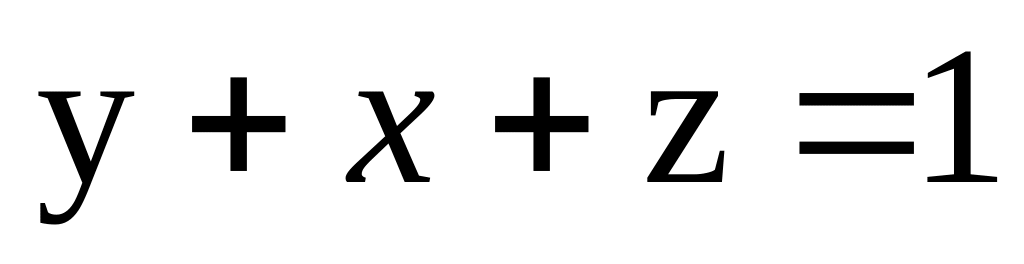 и координатными плоскостями. (Отв. 1/6).
и координатными плоскостями. (Отв. 1/6).Плоскостями у=0, z=0, 3х+у=6, 3х+2у=12, x+y+z=6. (Отв. 12).
Параболоидом вращения
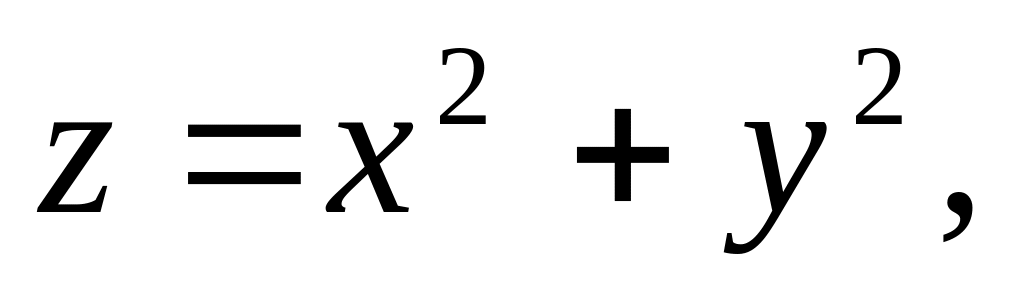 координатными плоскостями и плоскостью
х+у=1. (Отв.1/6).
координатными плоскостями и плоскостью
х+у=1. (Отв.1/6).Эллиптическим параболоидом и плоскостями z=0, у=1, у=2х, у=6-х. (Отв. 78
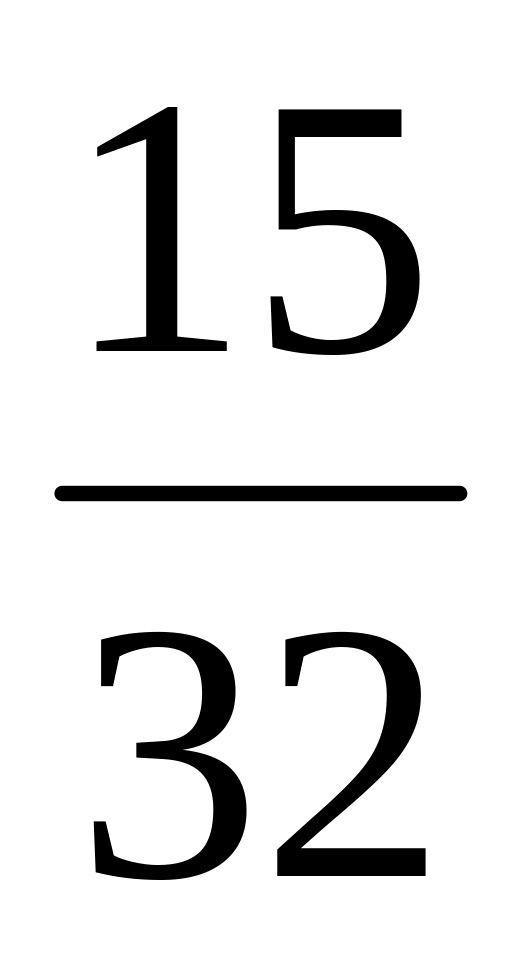 ).
).Цилиндрами
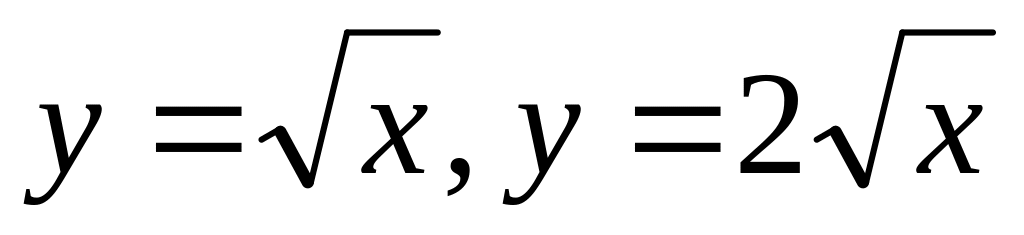 и плоскостями
и плоскостями
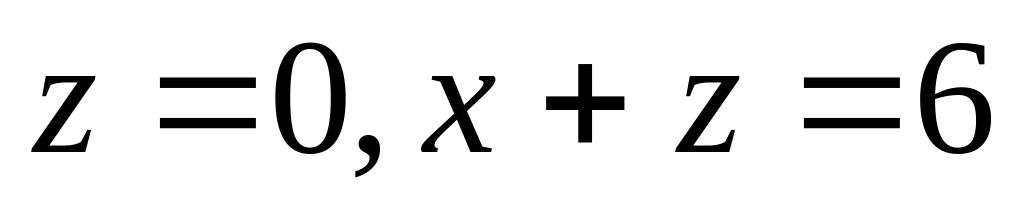 .
(Отв.
.
(Отв.
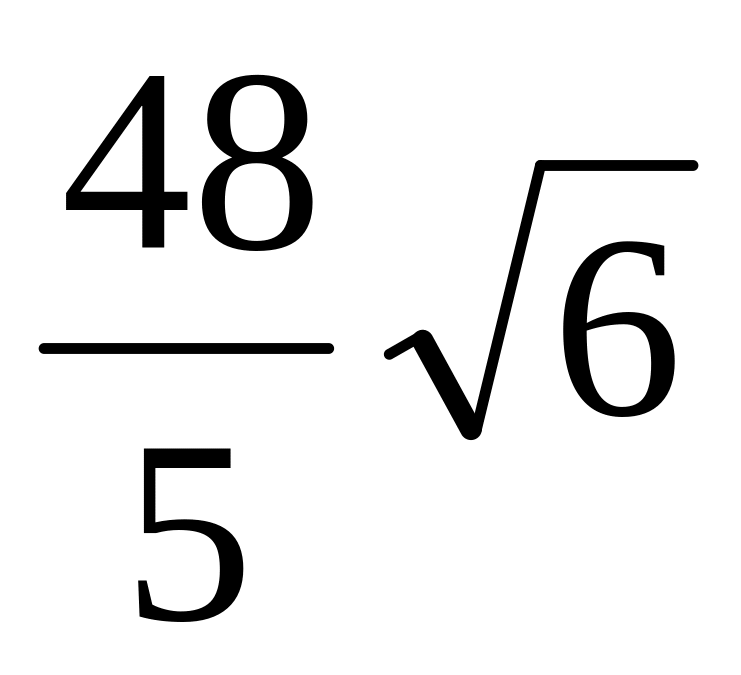 ).
).Цилиндром
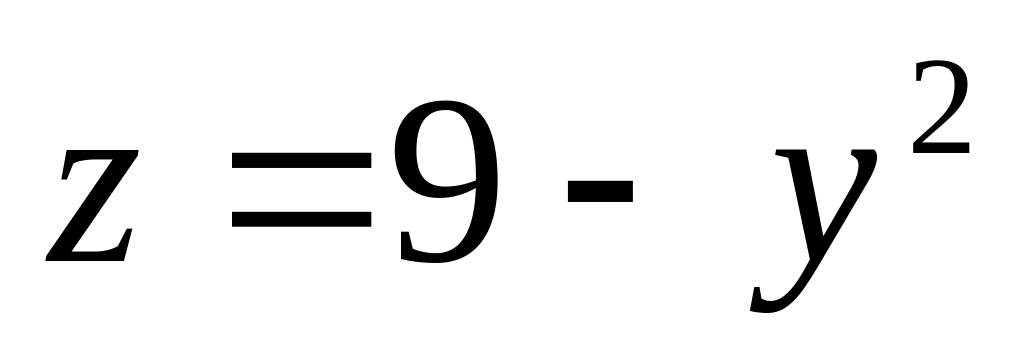 ,
координатными плоскостями и плоскостью
,
координатными плоскостями и плоскостью
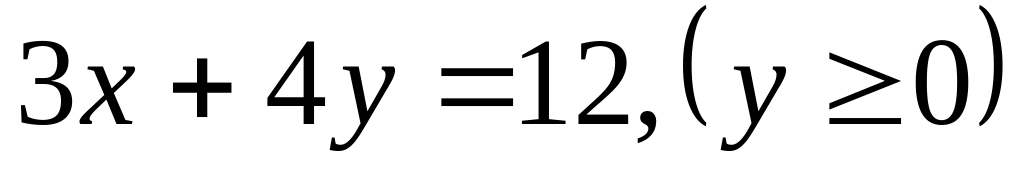 .
(Отв. 45).
.
(Отв. 45).Эллиптическим параболоидом плоскостями z=0, у=0, х=0, х+у=1. (Отв. 1/6)
Эллиптическим параболоидом цилиндром
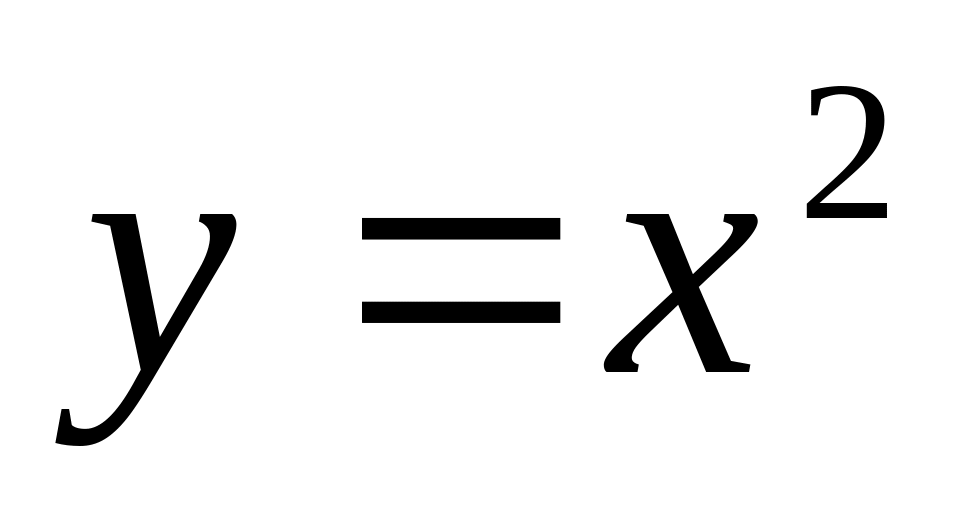 ,
плоскостями z=0, у=1. (Отв.
,
плоскостями z=0, у=1. (Отв.
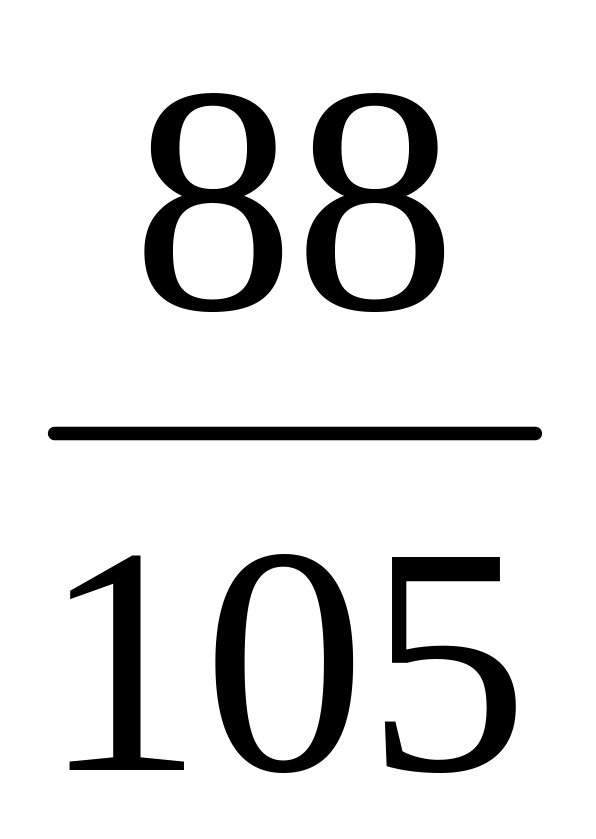 ).
).Параболоидом эллиптическим плоскостями z=0, у=0, х=0, х+у=1. (Отв. 1/6)
Плоскостями координат, плоскостями х=2, у=3 и эллиптическим параболоидом . (ответ 11)
Плоскостью и координатными плоскостями. (Отв. 1/6).
Плоскостями у=0, z=0, 3х+у=6, 3х+2у=12, x+y+z=6. (Отв. 12).
Параболоидом вращения координатными плоскостями и плоскостью х+у=1. (Отв.1/6).
Эллиптическим параболоидом и плоскостями z=0, у=1, у=2х, у=6-х. (Отв. 78 ).
Цилиндрами и плоскостями . (Отв. ).
Цилиндром , координатными плоскостями и плоскостью . (Отв. 45).
Эллиптическим параболоидом плоскостями z=0, у=0, х=0, х+у=1. (Отв. 1/6)
Эллиптическим параболоидом цилиндром , плоскостями z=0, у=1. (Отв. ).
Параболоидом эллиптическим плоскостями z=0, у=0, х=0, х+у=1. (Отв. 1/6).
Эллиптическим параболоидом и плоскостями z=0, у=1, у=2х, у=6-х. (Отв. 78 ).
Цилиндрами и плоскостями . (Отв. ).
Цилиндром , координатными плоскостями и плоскостью . (Отв. 45).
Эллиптическим параболоидом плоскостями z=0, у=0, х=0, х+у=1. (Отв. 1/6)
Эллиптическим параболоидом цилиндром , плоскостями z=0, у=1. (Отв. ).
Задание 6. Найти общее решение дифференциального уравнения.
а)
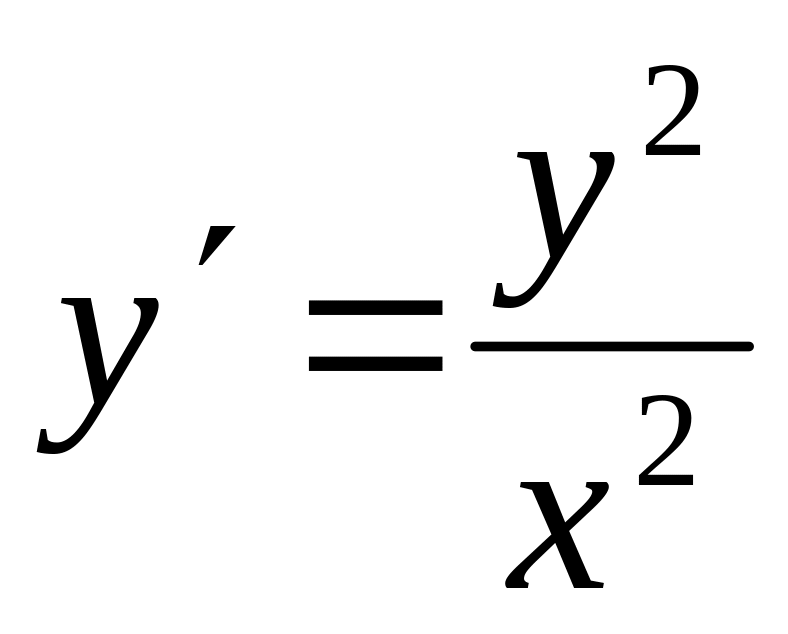 ;
б)
;
б)
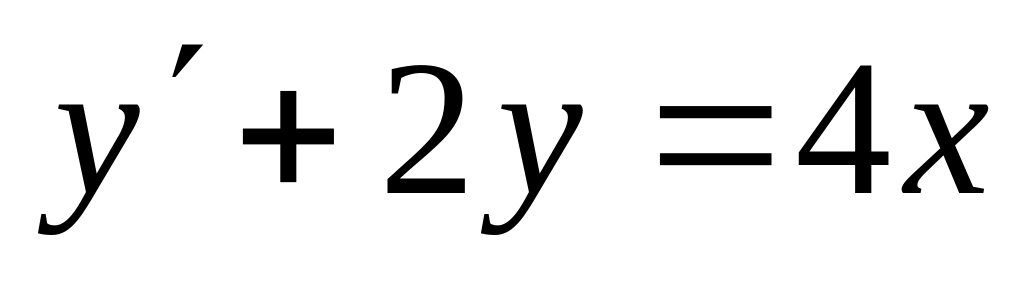 ;
;
а)
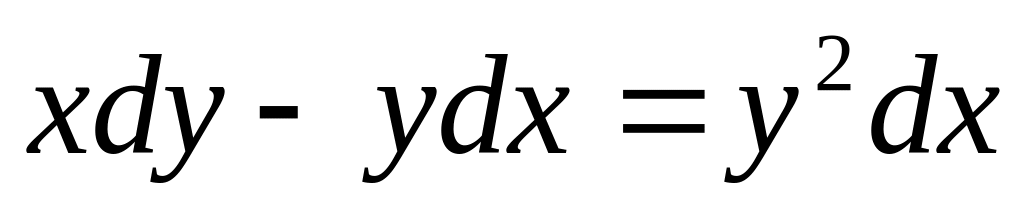 ; б)
; б)
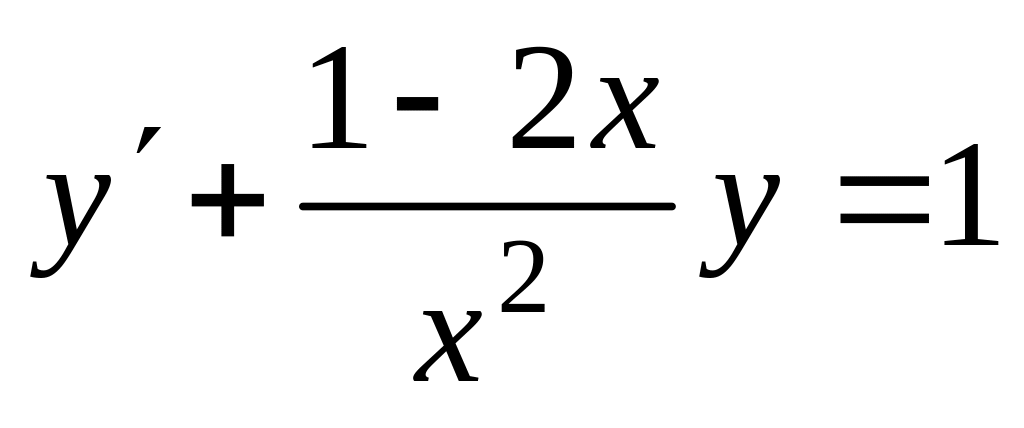 .
.а)
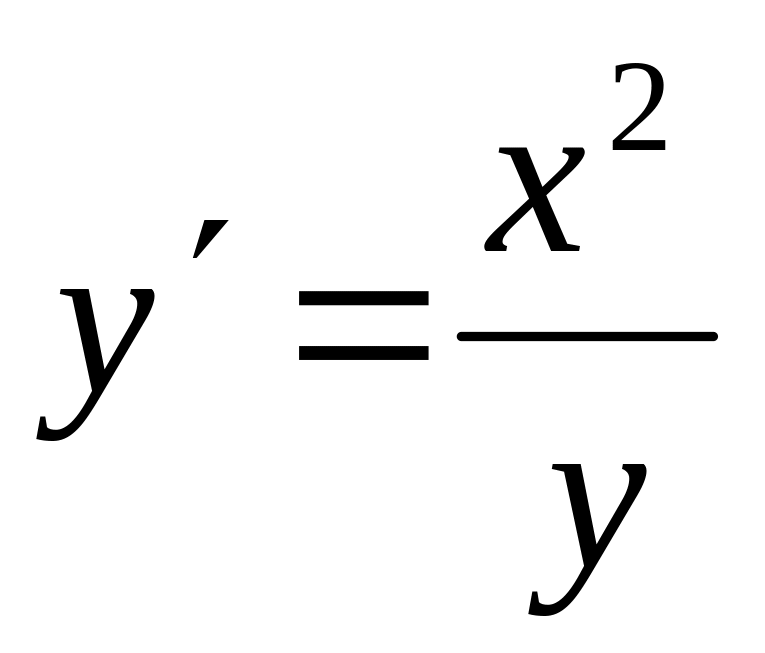 ;б)
;б)
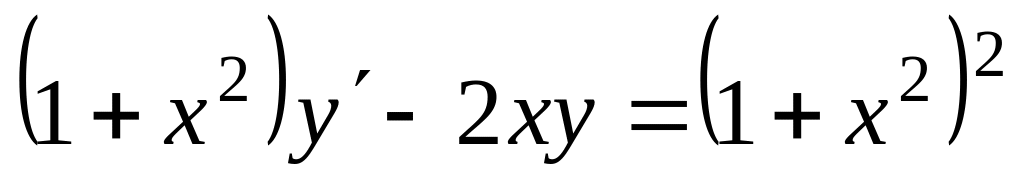 ;.
;.а)
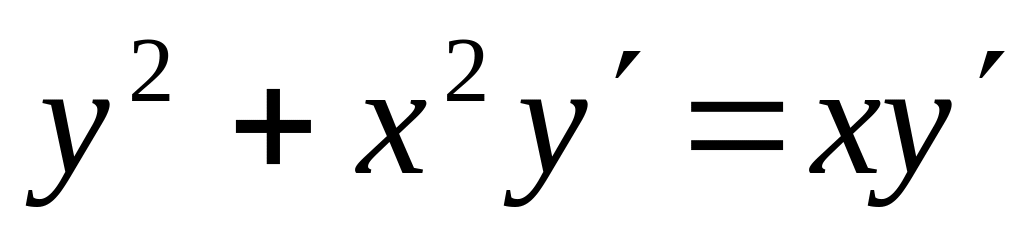 ; б)
; б)
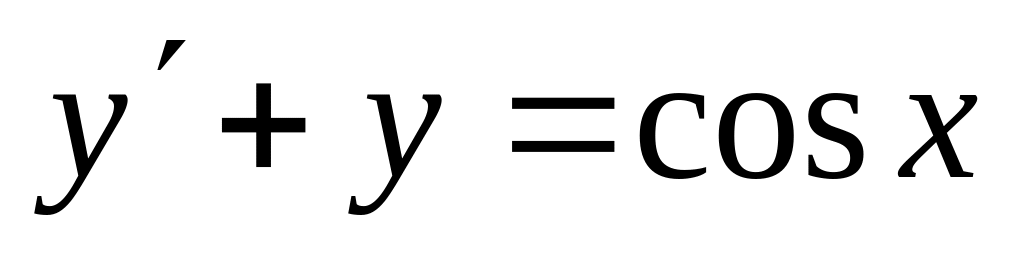 ;
;а)
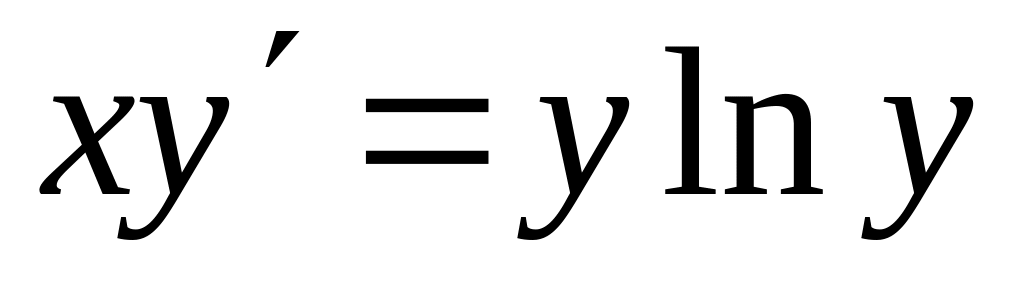 ; б)
; б)
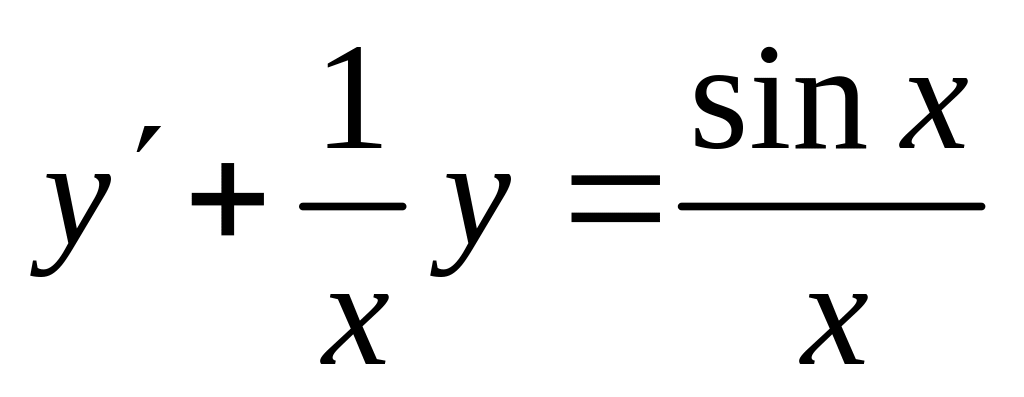 ;.
;.а)
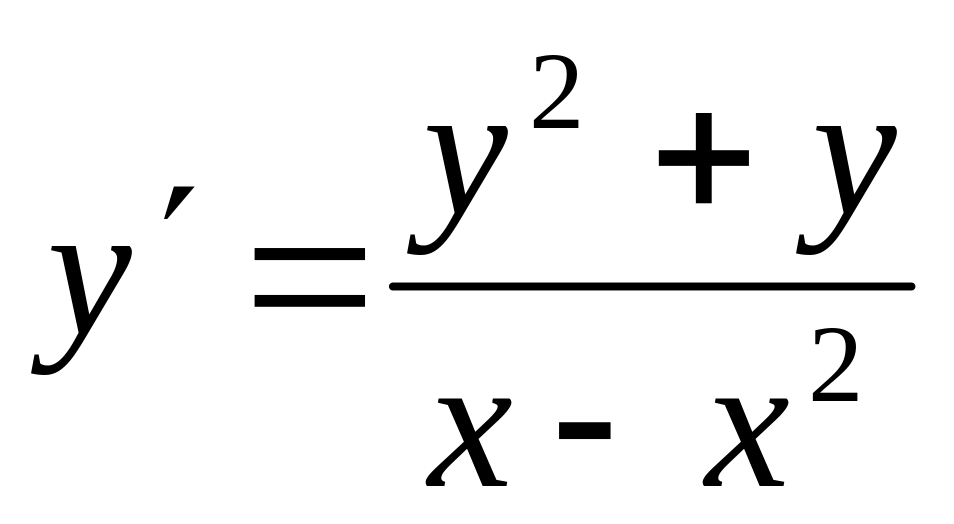 ; б)
; б)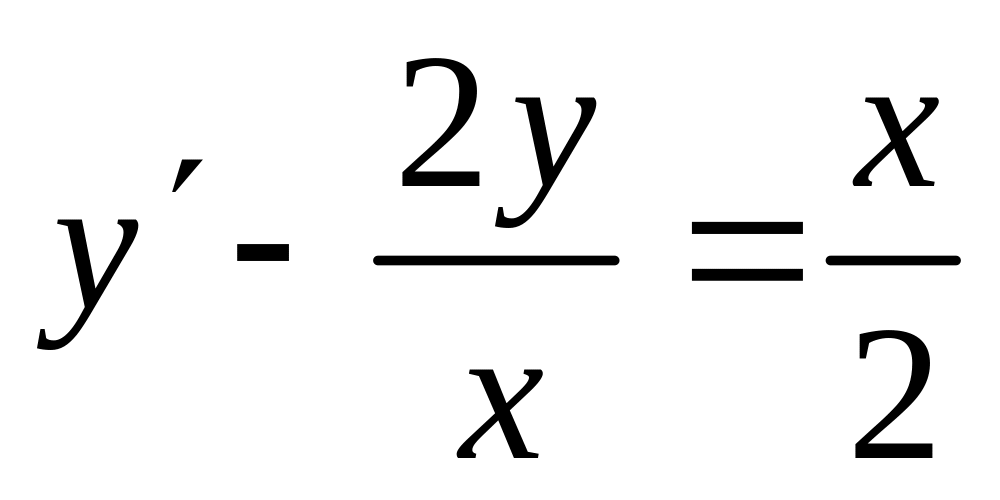 ; .
; .а)
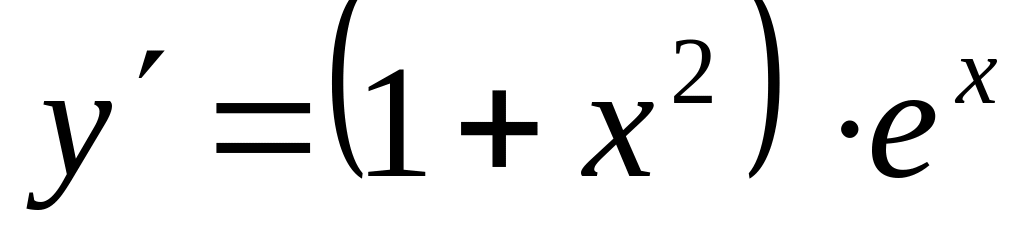 ;
б)
;
б)
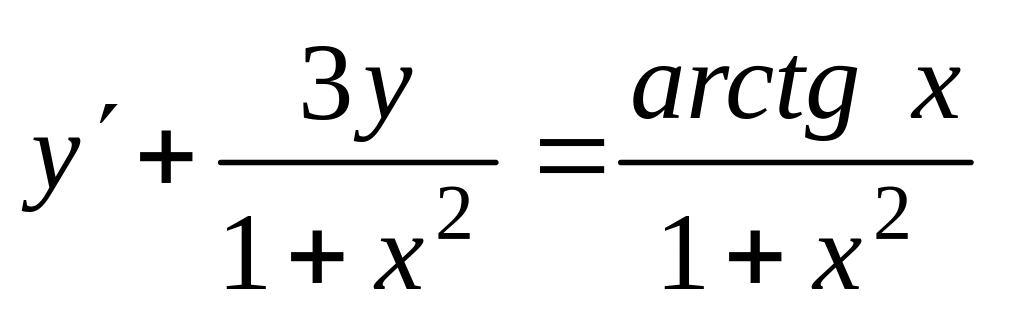 ;.
;.а)
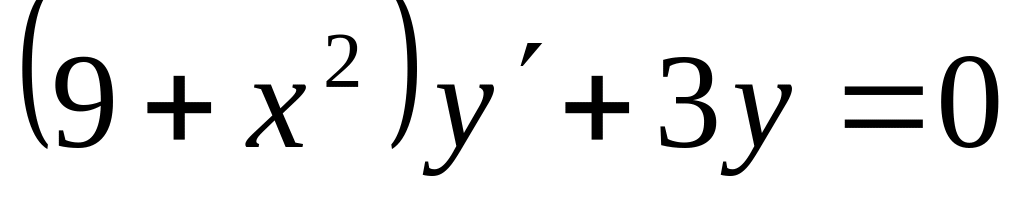 ; б)
; б)
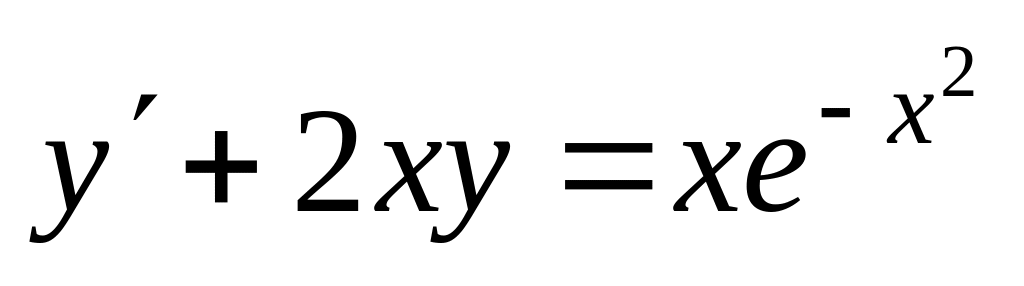 ;
;
а)
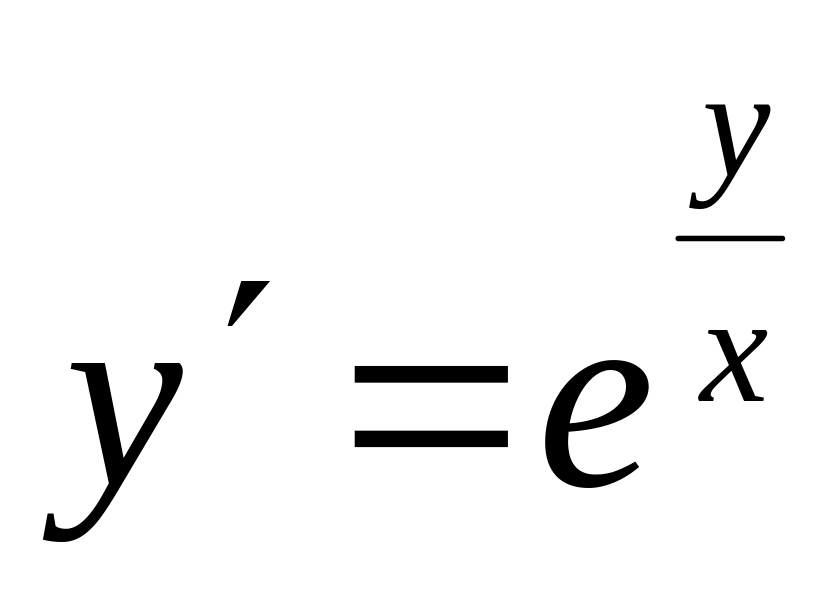 ; б)
; б)
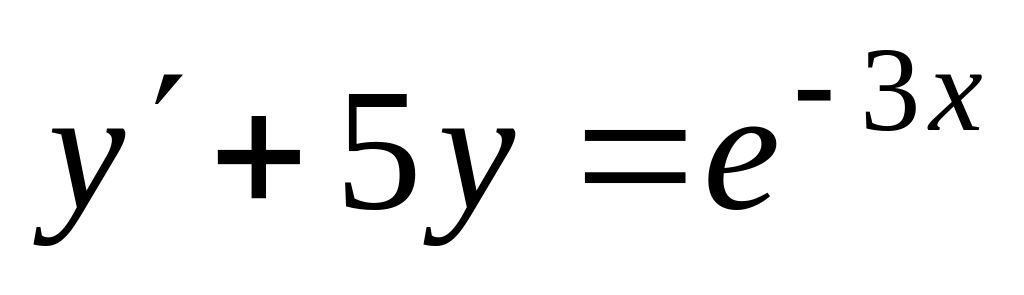 ;
; а) ; б)
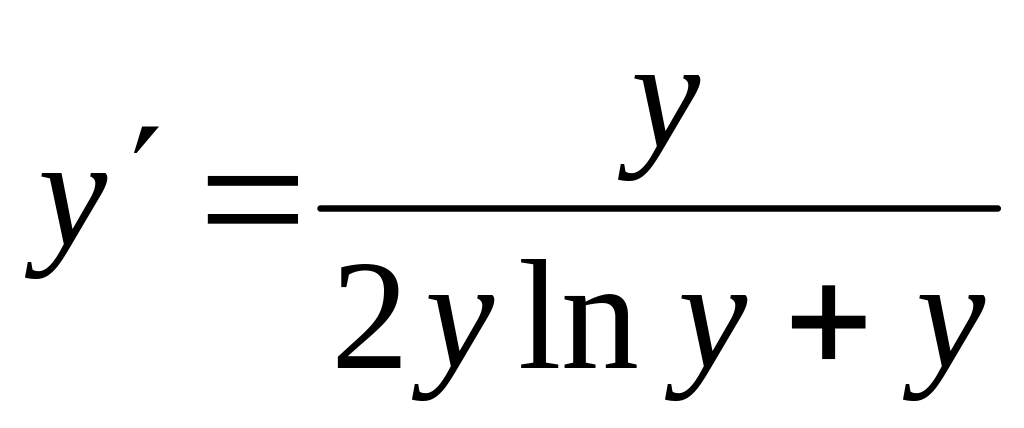 ;
;
а) ; б) ;
а) ; б) .
а) ;б) ;.
а) ; б) ;
а) ; б) ;.
а) ; б) ; .
а) ; б) ;.
а) ; б) ;
а) ; б) ;
20. а) ; б) ;
21. а) ; б) ;
22. а) ; б) .
23. а) ;б) ;.
24. а) ; б) ;
25 а) ; б) ;.
Задание 7. Для данного дифференциального уравнения второго порядка найти частное решение, удовлетворяющее заданным начальным условиям.
1.
![]() ,
,
![]() ,
,
![]() .
.
2.
![]() ,
,
![]() .
.
3.
![]() ,
,
![]() ,
,
![]() .
.
4.
![]() ,
,
![]() ,
,
![]() .
.
5.
![]() ,
,
![]() ,
.
,
.
6.
![]() ,
,
![]() ,
,
![]() .
.
7.
![]() ,
,
![]() ,
,
![]() .
.
8.
![]() ,
,
.
,
,
.
9. , , .
10.
![]() ,
,
![]() .
.
11. , , .
12. , .
13. , , .
14. , , .
15. , , .
16. , , .
17. , , .
18. , , .
19. , , .
20. , .
21. , , .
22. , .
23. , , .
24. , , .
25. , , .
Задание 8. Исследовать на сходимость ряды.
1. а)
![]() ;
б)
;
б)
![]() в)
в)
![]() ; г)
; г)
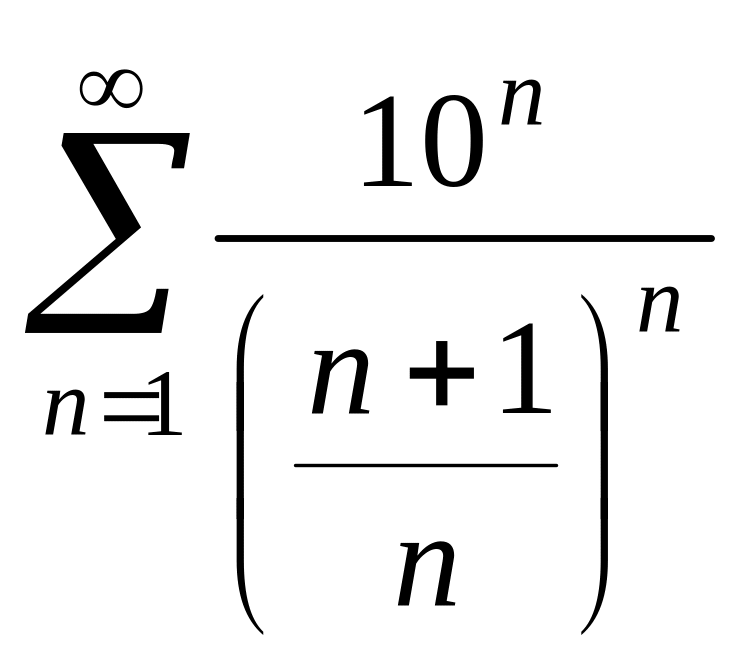 .
.
2. а)
![]() ; б)
; б)
![]() ; в)
; в)
![]() ; г)
; г)
![]() .
.
3. а)
![]() ; б)
; б)
![]() ; в)
; в)
![]() ; г)
; г)
![]() .
.
4. а)
![]() ; б)
; б)
![]() ; в)
; в)
![]() ; г)
; г)
![]() .
.
5. а)
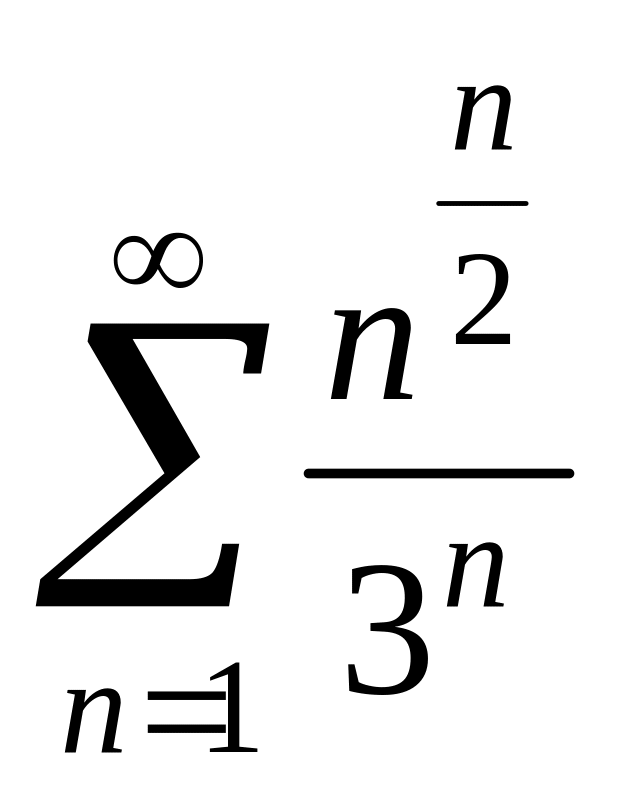 ; б)
; б)
![]() ; в)
; в)
![]() ; г)
; г)
![]() .
.
6. а)
![]() ; б)
; б)
![]() ; в)
; в)
![]() ; г)
; г)
![]() .
.
7. а)
![]() ; б)
; б)
![]() ; в)
; в)
![]() ; г)
; г)
![]() .
.
8. а)
![]() ; б)
; б)
![]() ; в)
; в)
![]() ; г)
; г)
![]() .
.
9. а)
![]() ; б)
; б)
![]() ; в)
; в)
![]() ; г)
; г)
![]() .
.
10. а)
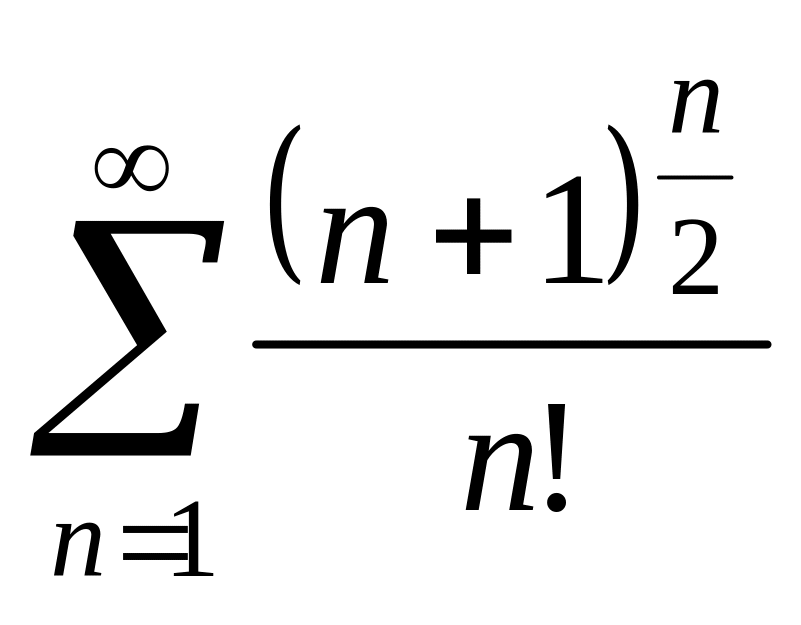 ; б)
; б)
![]() ; в)
; в)
![]() ;г)
;г)
![]() .
.
11. а) ; б) в) ; г) .
12. а) ; б) ; в) ; г) .
13. а) ; б) ; в) ; г) .
14. а) ; б) ; в) ; г) .
15. а) ; б) ; в) ; г) .
16. а) ; б) ; в) ; г) .
17. а) ; б) ; в) ; г) .
18. а) ; б) ; в) ; г) .
19. а) ; б) ; в) ; г) .
20. а) ; б) ; в) ;г) .
21. а) ; б) в) ; г) .
22. а) ; б) ; в) ; г) .
23. а) ; б) ; в) ; г) .
24. а) ; б) ; в) ; г) .
25. а) ; б) ; в) ; г) .
Задание
9.
Разложить в ряд Фурье функцию
![]() на отрезке
на отрезке
![]() .
.
1.
![]()
2.
![]()
3.
![]()
4.
![]()
5.
![]()
6.
![]()
7.
![]()
8.
![]()
9.
![]()
10.
![]()
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23
24.
25.
___________________________________________________________________________
